(人教A版)数学必修四 1.1.1 任意角 课件
文档属性
| 名称 | (人教A版)数学必修四 1.1.1 任意角 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 921.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-06 00:00:00 | ||
图片预览











文档简介
课件31张PPT。第一章 三角函数第一章 三角函数1.1 任意角和弧度制
1.1.1 任意角第一章 算法初步学习导航
1.任意角
(1)角的概念
角可以看成平面内一条_______绕着端点从一个位置______到
另一个位置所成的________
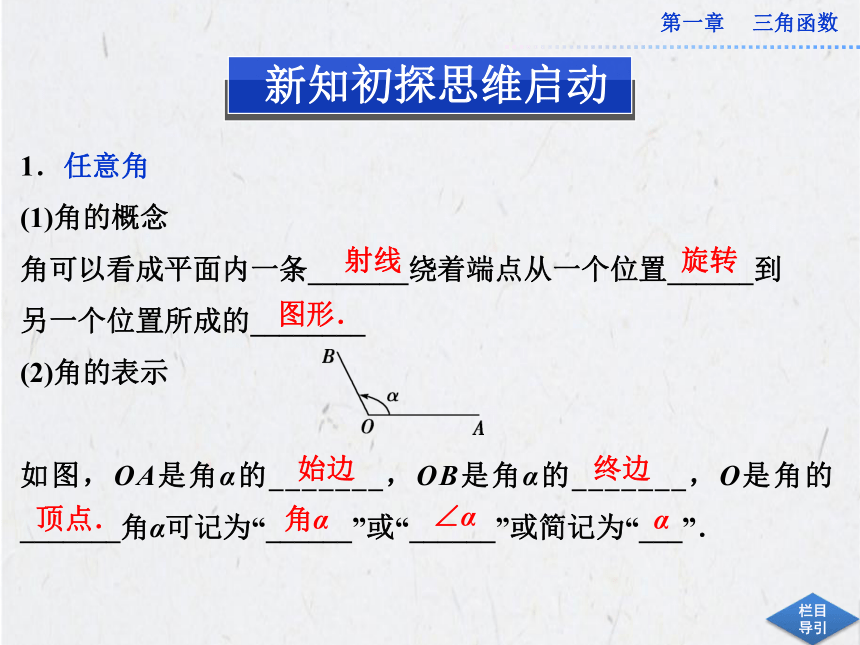
(2)角的表示
如图,OA是角α的_______,OB是角α的_______,O是角的_______角α可记为“______”或“______”或简记为“___”.射线旋转图形.始边终边顶点.角α∠αα(3)角的分类
按旋转方向,角可以分为三类:
逆时针顺时针想一想
1.理解角的概念要注意哪几个要素?
提示:顶点,始边,终边和旋转方向.
做一做
1.图中OA为始边,则α=________,β=________.
答案:140° -220°
2.象限角
把角放在平面直角坐标系中,使角的顶点与________
重合,角的始边与___轴的非负半轴重合,那么角的_____在第几象限,就说这个角是第几____________;如果角的终边在__________,就认为这个角不属于任何一个象限.
原点终边x象限角坐标轴上2.判断下列说法是否正确.
(1)第一象限角都是锐角( )
(2)锐角都是第一象限角( )
(3)第一象限角一定不是负角( )
(4)第二象限角是钝角( )
答案:(1)× (2)√ (3)× (4)×
3.终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=___________________},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
α+k·360°,k∈Z想一想
2.终边相同的角一定相等吗?相等的角终边一定相同吗?
提示:终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差周角的整数倍.
做一做
3.(1)在0°~360°内与390°终边相同角为________.
(2)与45°角终边相同的角是________.
答案:(1)30° (2)45°+k·360°,k∈Z
题型一 任意角的概念
下列命题:
①第二象限角大于第一象限角;
②小于180°的角是钝角、直角或锐角;
③正角大于负角;④相差360°整数倍的两个角,其终边不一定相同.
其中真命题的序号为________(把你认为正确的命题的序号都写上).
【解析】 ①120°角是第二象限角,390°角是第一象限角,
显然390°>120°,所以①不正确.
②0°角小于180°,但它既不是钝角,也不是直角或锐角,
故②不正确.
③正角、负角是用来表示具有相反意义的旋转量,像正数、
负数的规定一样,正角大于负角,③正确.
④终边相同的两个角一定相差360°的整数倍,反之也成立,
故④不正确.【答案】 ③
【名师点评】 解决此类问题的关键在于正确理解0°~90°的角、象限角、锐角、小于90°的角等概念.另外需要掌握判断命题真假的技巧:判断命题为真时需要证明,而判断命题为假时只要举出反例即可.
跟踪训练
1.A={小于90°的角},B={第一象限角},则A∩B=( )
A.{锐角} B.{小于90°的角}
C.{第一象限角} D.以上都不对
解析:选D.小于90°的角由锐角、零角、负角组成,而第一象限的角包含有锐角及其他终边在第一象限的角,所以A∩B是由锐角和终边在第一象限的负角组成的集合,故选D.
题型二 终边相同的角及象限角 下列各角分别是第几象限角?请写出与下列各角的终边相同的角的集合S,并把S中适合不等式-360°≤β<720°的元素β写出来:
(1)60°;(2)-21°;(3)363°14′.
【解】 (1)60°是第一象限角,S={β|β=60°+k·360°,k∈Z},S中适合-360°≤β<720°的元素是60°+(-1)×360°=-300°,60°+0×360°=60°,60°+1×360°=420°.(2)-21°是第四象限角,S={β|β=-21°+k·360°,k∈Z},S中适合-360°≤β<720°的元素是-21°+0×360°=-21°,-21°+1×360°=339°,-21°+2×360°=699°.
(3)363°14′是第一象限角,S={β|β=363°14′+k·360°,k∈Z},S中适合-360°≤β<720°的元素是363°14′
+(-2)×360°=-356°46′,363°14′+(-1)×360°
=3°14′,363°14′+0×360°=363°14′.
【名师点评】 (1)象限角的判定有两种方法:一是根据图象;二是将角转化到0°~360°范围内,利用图象实际操作时,依据的还是终边相同的角的思想.
(2)终边相同的角之间相差360°的整数倍,终边在同一直线上的角之间相差180°的整数倍,终边在相互垂直的两直线上的角之间相差90°的整数倍.
跟踪训练
2.(1)已知α是第二象限角,则180°+α是第________象限角,-α是第________象限角.答案:四 三
(2)已知α=-1 910°.
①把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,指出它是第几象限角;
②求θ,使θ与α的终边相同,且-720°≤θ<0°.解:①-1 910°=250°+(-6)×360°,∵250°是第三象限角,∴α=-1 910°是第三象限角.
②令θ=250°+k·360°(k∈Z),由-720°≤250°+k·360°<0°得-2≤k≤-1,∴k=-2,-1,此时θ=-470°,-110°.
题型三 区域角的表示
已知角α的终边落在阴影所表示的范围内(包括边界),试写出角α的集合.【解】 在0°~360°范围内,终边落在阴影内的角为90°≤α≤135°或 270°≤α≤315°.所以终边落在阴影所表示的范围内的角α的集合为{α|90°+k·360°≤α≤135°+k·360°,k∈Z}∪{α|270°+k·360°≤α≤315°+k·360°,k∈Z}={α|90°+2k·180°≤α≤135°+2k·180°,k∈Z}∪{α|90°+(2k+1)·180°≤α≤135°+(2k+1)·180°,k∈Z}={α|90°+n·180°≤α≤135°+n·180°,n∈Z}.【名师点评】 表示区间角的三个步骤:
第一步:先按逆时针的方向找到区域的起始和终止边界;
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α第三步:起始、终止边界对应角α,β再加上360°的整数倍,即得区间角集合.跟踪训练
3.
如右图,
(1)终边落在OB位置,且在-360°≤β≤360°内的角β的集合是________.
(2)终边落在阴影部分(含边界)的角的集合是________.
(3)终边落在阴影部分(含边界)且在0°≤β≤360°内的角β的集合是________.
(4)终边不落在阴影部分(含边界)的角的集合是________.答案:(1){-45°,315°}
(2){β|-45°+k·360°≤β≤120°+k·360°,k∈Z}
(3){β|0°≤β≤120°或315°≤β≤360°}
(4){β|-240°+k·360°<β<-45°+k·360°,k∈Z}1.对角的概念的认识关键是抓住“旋转”二字
(1)要明确旋转方向;
(2)要明确旋转的大小;
(3)要明确射线未作任何旋转时的位置.2.终边相同的角的四个注意点
所有与角α终边相同的角,连同角α在内可以用式子α+k·360°,k∈Z表示,在运用时需注意以下几点:
(1)k是整数,这个条件不能漏掉;
(2)α是任意角;
(3)k·360°与α之间用“+”连接,如k·360°-30°应看成-30°+k·360°,k∈Z;
(4)终边相同的角不一定相等,终边相同的角有无数个,它们相差周角的整数倍.相等的角终边一定相同.名师解题互动探究解:因为α是第二象限角,所以90°+k·360°<α<180°+k·360°(k∈Z).
(1)因为180°+2k·360°<2α<360°+2k·360°(k∈Z),故2α是第三或第四象限角或终边落在y轴非正半轴的角.
1.1.1 任意角第一章 算法初步学习导航
1.任意角
(1)角的概念
角可以看成平面内一条_______绕着端点从一个位置______到
另一个位置所成的________
(2)角的表示
如图,OA是角α的_______,OB是角α的_______,O是角的_______角α可记为“______”或“______”或简记为“___”.射线旋转图形.始边终边顶点.角α∠αα(3)角的分类
按旋转方向,角可以分为三类:
逆时针顺时针想一想
1.理解角的概念要注意哪几个要素?
提示:顶点,始边,终边和旋转方向.
做一做
1.图中OA为始边,则α=________,β=________.
答案:140° -220°
2.象限角
把角放在平面直角坐标系中,使角的顶点与________
重合,角的始边与___轴的非负半轴重合,那么角的_____在第几象限,就说这个角是第几____________;如果角的终边在__________,就认为这个角不属于任何一个象限.
原点终边x象限角坐标轴上2.判断下列说法是否正确.
(1)第一象限角都是锐角( )
(2)锐角都是第一象限角( )
(3)第一象限角一定不是负角( )
(4)第二象限角是钝角( )
答案:(1)× (2)√ (3)× (4)×
3.终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=___________________},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
α+k·360°,k∈Z想一想
2.终边相同的角一定相等吗?相等的角终边一定相同吗?
提示:终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差周角的整数倍.
做一做
3.(1)在0°~360°内与390°终边相同角为________.
(2)与45°角终边相同的角是________.
答案:(1)30° (2)45°+k·360°,k∈Z
题型一 任意角的概念
下列命题:
①第二象限角大于第一象限角;
②小于180°的角是钝角、直角或锐角;
③正角大于负角;④相差360°整数倍的两个角,其终边不一定相同.
其中真命题的序号为________(把你认为正确的命题的序号都写上).
【解析】 ①120°角是第二象限角,390°角是第一象限角,
显然390°>120°,所以①不正确.
②0°角小于180°,但它既不是钝角,也不是直角或锐角,
故②不正确.
③正角、负角是用来表示具有相反意义的旋转量,像正数、
负数的规定一样,正角大于负角,③正确.
④终边相同的两个角一定相差360°的整数倍,反之也成立,
故④不正确.【答案】 ③
【名师点评】 解决此类问题的关键在于正确理解0°~90°的角、象限角、锐角、小于90°的角等概念.另外需要掌握判断命题真假的技巧:判断命题为真时需要证明,而判断命题为假时只要举出反例即可.
跟踪训练
1.A={小于90°的角},B={第一象限角},则A∩B=( )
A.{锐角} B.{小于90°的角}
C.{第一象限角} D.以上都不对
解析:选D.小于90°的角由锐角、零角、负角组成,而第一象限的角包含有锐角及其他终边在第一象限的角,所以A∩B是由锐角和终边在第一象限的负角组成的集合,故选D.
题型二 终边相同的角及象限角 下列各角分别是第几象限角?请写出与下列各角的终边相同的角的集合S,并把S中适合不等式-360°≤β<720°的元素β写出来:
(1)60°;(2)-21°;(3)363°14′.
【解】 (1)60°是第一象限角,S={β|β=60°+k·360°,k∈Z},S中适合-360°≤β<720°的元素是60°+(-1)×360°=-300°,60°+0×360°=60°,60°+1×360°=420°.(2)-21°是第四象限角,S={β|β=-21°+k·360°,k∈Z},S中适合-360°≤β<720°的元素是-21°+0×360°=-21°,-21°+1×360°=339°,-21°+2×360°=699°.
(3)363°14′是第一象限角,S={β|β=363°14′+k·360°,k∈Z},S中适合-360°≤β<720°的元素是363°14′
+(-2)×360°=-356°46′,363°14′+(-1)×360°
=3°14′,363°14′+0×360°=363°14′.
【名师点评】 (1)象限角的判定有两种方法:一是根据图象;二是将角转化到0°~360°范围内,利用图象实际操作时,依据的还是终边相同的角的思想.
(2)终边相同的角之间相差360°的整数倍,终边在同一直线上的角之间相差180°的整数倍,终边在相互垂直的两直线上的角之间相差90°的整数倍.
跟踪训练
2.(1)已知α是第二象限角,则180°+α是第________象限角,-α是第________象限角.答案:四 三
(2)已知α=-1 910°.
①把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,指出它是第几象限角;
②求θ,使θ与α的终边相同,且-720°≤θ<0°.解:①-1 910°=250°+(-6)×360°,∵250°是第三象限角,∴α=-1 910°是第三象限角.
②令θ=250°+k·360°(k∈Z),由-720°≤250°+k·360°<0°得-2≤k≤-1,∴k=-2,-1,此时θ=-470°,-110°.
题型三 区域角的表示
已知角α的终边落在阴影所表示的范围内(包括边界),试写出角α的集合.【解】 在0°~360°范围内,终边落在阴影内的角为90°≤α≤135°或 270°≤α≤315°.所以终边落在阴影所表示的范围内的角α的集合为{α|90°+k·360°≤α≤135°+k·360°,k∈Z}∪{α|270°+k·360°≤α≤315°+k·360°,k∈Z}={α|90°+2k·180°≤α≤135°+2k·180°,k∈Z}∪{α|90°+(2k+1)·180°≤α≤135°+(2k+1)·180°,k∈Z}={α|90°+n·180°≤α≤135°+n·180°,n∈Z}.【名师点评】 表示区间角的三个步骤:
第一步:先按逆时针的方向找到区域的起始和终止边界;
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α
3.
如右图,
(1)终边落在OB位置,且在-360°≤β≤360°内的角β的集合是________.
(2)终边落在阴影部分(含边界)的角的集合是________.
(3)终边落在阴影部分(含边界)且在0°≤β≤360°内的角β的集合是________.
(4)终边不落在阴影部分(含边界)的角的集合是________.答案:(1){-45°,315°}
(2){β|-45°+k·360°≤β≤120°+k·360°,k∈Z}
(3){β|0°≤β≤120°或315°≤β≤360°}
(4){β|-240°+k·360°<β<-45°+k·360°,k∈Z}1.对角的概念的认识关键是抓住“旋转”二字
(1)要明确旋转方向;
(2)要明确旋转的大小;
(3)要明确射线未作任何旋转时的位置.2.终边相同的角的四个注意点
所有与角α终边相同的角,连同角α在内可以用式子α+k·360°,k∈Z表示,在运用时需注意以下几点:
(1)k是整数,这个条件不能漏掉;
(2)α是任意角;
(3)k·360°与α之间用“+”连接,如k·360°-30°应看成-30°+k·360°,k∈Z;
(4)终边相同的角不一定相等,终边相同的角有无数个,它们相差周角的整数倍.相等的角终边一定相同.名师解题互动探究解:因为α是第二象限角,所以90°+k·360°<α<180°+k·360°(k∈Z).
(1)因为180°+2k·360°<2α<360°+2k·360°(k∈Z),故2α是第三或第四象限角或终边落在y轴非正半轴的角.
