第十章:数据的收集、整理与描述练习题2021-2022学年贵州省七年级下学期人教版数学期末试题选编(含解析)
文档属性
| 名称 | 第十章:数据的收集、整理与描述练习题2021-2022学年贵州省七年级下学期人教版数学期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 628.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 09:09:02 | ||
图片预览



文档简介
第十章:数据的收集、整理与描述练习题
一、单选题
1.(2022春·贵州黔南·七年级统考期末)要调查太原市中学生对垃圾分类知识的了解情况,下列调查方式最适合的是( )
A.在太原市迎泽区某中学随机抽取名学生进行调查
B.在太原市所有中学男生中随机抽取名进行调查
C.在太原市所有中学初三年级中随机抽取名学生进行调查
D.在太原市所有中学生中随机抽取名学生进行调查
2.(2022春·贵州贵阳·七年级统考期末)要调查某区九年级 8000 名学生对“双减”政策的了解情况,下列调查方式最合适的是( )
A.在某校九年级学生中随机选取50名学生
B.在全区 8000 名九年级学生中随机选取800名学生
C.在全区 8000 名九年级学生中随机选取800名男生
D.在全区 8000 名九年级学生中随机选取800名女生
3.(2022春·贵州遵义·七年级统考期末)下列调查中,适合全面调查的是( )
A.了解某市中学生视力情况 B.第七次全国人口普查
C.了解一批灯泡的使用寿命 D.调查春节联欢晚会的收视率
4.(2022春·贵州黔西·七年级统考期末)要了解七年级1500名学生的心理健康情况,从中抽取了300名学生的心理健康评估报告进行统计分析,其中“抽取的每名学生的心理健康评估报告”是( )
A.总体 B.个体 C.样本 D.样本容量
5.(2022春·贵州贵阳·七年级统考期末)下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.
以上数据摘自《“一带一路”贸易合作大数据报告(2017)》,根据统计图提供的信息,下列推断不合理的是( )
A.与2015年相比,2016年我国与东欧地区的贸易额有所增长
B.2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多
C.2011-2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元
D.2011-2016年,我国与东南亚地区的贸易额逐年增长
6.(2022春·贵州遵义·七年级统考期末)已知数据35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34,在列频数分布表时,如果取组距为2,那么应分成组数为( )
A.4 B.5 C.6 D.7
7.(2022春·贵州黔南·七年级统考期末)某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图.那么仰卧起坐次数在25~30次的人数是( )
A.3人 B.5人 C.10人 D.12人
二、填空题
8.(2022春·贵州黔东南·七年级统考期末)为了解某地区七年级8460名学生中会游泳的学生人数,随机调查了其中400名学生,结果有150名学生会游泳,样本容量是 ________ .
9.(2022春·贵州黔南·七年级统考期末)某班级有45名学生参加了期中考试,分数段在70~79分的占比为40%,则该班级在这个分数段内的学生有_________人.
10.(2022春·贵州安顺·七年级统考期末)一次数学单元测试后,全班50名学生的成绩被分成5组,第1-4组的频数分别是18,10,12,4,则第五组的数率是___.
三、解答题
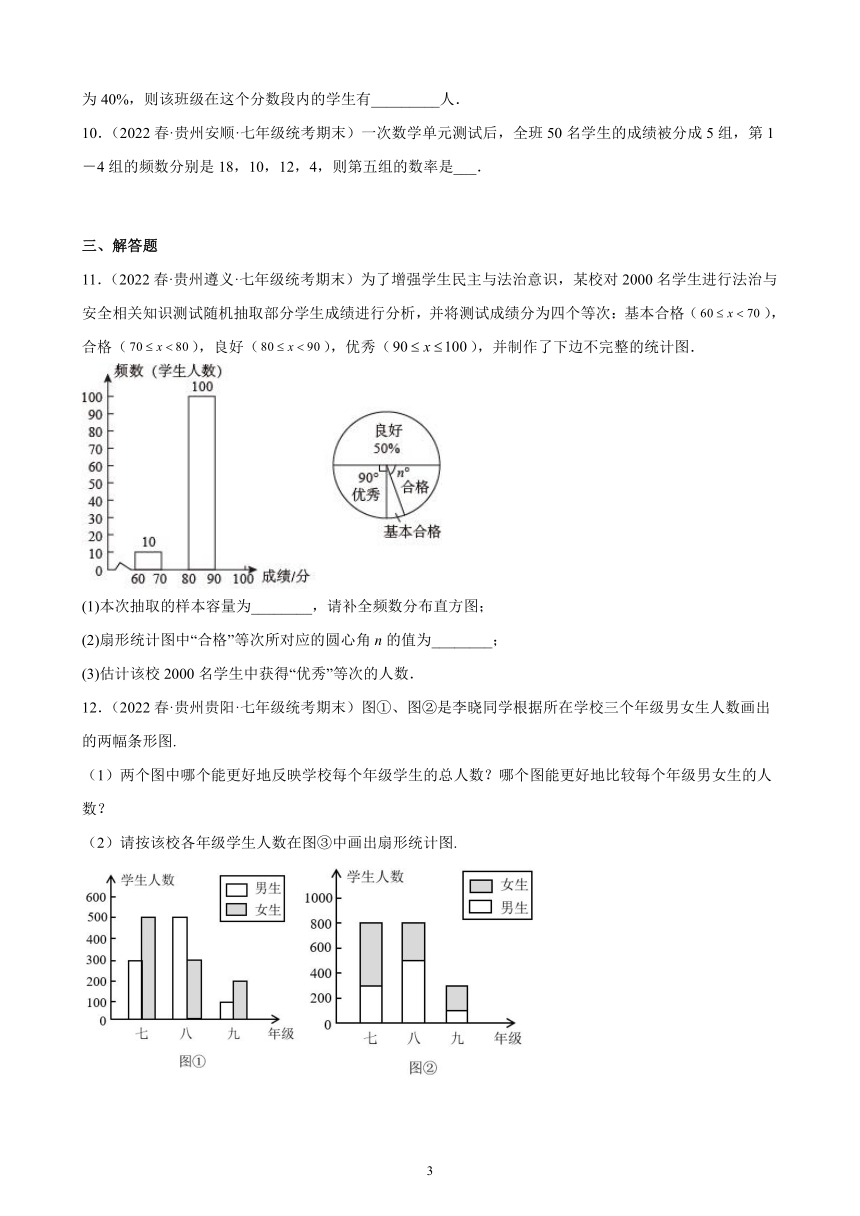
11.(2022春·贵州遵义·七年级统考期末)为了增强学生民主与法治意识,某校对2000名学生进行法治与安全相关知识测试随机抽取部分学生成绩进行分析,并将测试成绩分为四个等次:基本合格(),合格(),良好(),优秀(),并制作了下边不完整的统计图.
(1)本次抽取的样本容量为________,请补全频数分布直方图;
(2)扇形统计图中“合格”等次所对应的圆心角n的值为________;
(3)估计该校2000名学生中获得“优秀”等次的人数.
12.(2022春·贵州贵阳·七年级统考期末)图①、图②是李晓同学根据所在学校三个年级男女生人数画出的两幅条形图.
(1)两个图中哪个能更好地反映学校每个年级学生的总人数?哪个图能更好地比较每个年级男女生的人数?
(2)请按该校各年级学生人数在图③中画出扇形统计图.
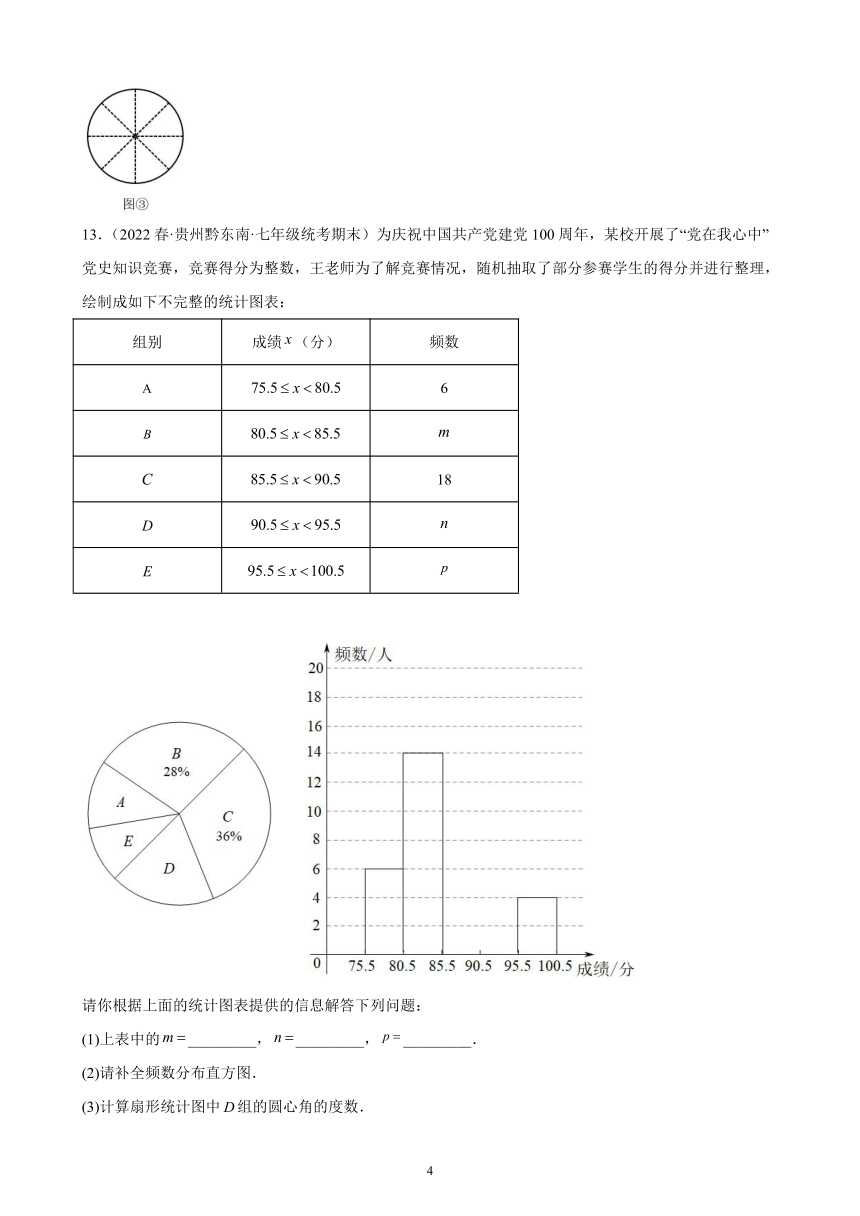
13.(2022春·贵州黔东南·七年级统考期末)为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成如下不完整的统计图表:
组别 成绩(分) 频数
6
18
请你根据上面的统计图表提供的信息解答下列问题:
(1)上表中的_________,_________,_________.
(2)请补全频数分布直方图.
(3)计算扇形统计图中组的圆心角的度数.
(4)已知该校有1000名学生,请估计竞赛成绩在90分以上(不含90分)的学生有多少人?
14.(2022春·贵州黔东南·七年级统考期末)某学校为了解《大中小学劳动教育指导纲要(试行)》落实情况,就假期“平均每天帮助父母干家务所用时长”进行了调查,如图是根据相关数据绘制的统计图的一部分根据上述信息,回答下列问题:
(1)在本次随机抽取的样本中,调查的学生人数是多少?
(2)补全扇形统计图和频数分布直方图:
(3)如果该校共有学生3000人,请你估计“平均每天帮助父母干家务所用时长不少于30分钟”的学生大约有多少人?
15.(2022春·贵州遵义·七年级统考期末)为了加强学生的交通安全意识,遵义交利用微信公众号发布了交通安全知识在线测试从中抽取了部分学生在线测试成绩(分数取正整数,满分为100分)进行统计,绘制了下面不完整的频数分布直方图和扇形统计图,根据图中提供的信息解答下列问题:
(1)求样本容量和a的值;
(2)求D等级对应扇形圆心角的度数;
(3)补全频数分布直方图;
(4)若交通安全知识在线测试成绩在80分以上为优秀,某学校共有1800名学生,估计该校成绩优秀的学生约为多少名?
16.(2022春·贵州安顺·七年级统考期末)某县举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生被分为5组,同时听写100个汉字,每正确听写出一个汉字得1分.根据决赛成绩绘制出部分频数分布表和部分频数分布直方图如下.
组别 成绩x分 频数(人数)
第1组 4
第2组 8
第3组 16
第4组 a
第5组 10
根据以上信息,解决下列问题:
(1)频数分布表中a=________;
(2)请补全频数分布直方图.
(3)若决赛成绩不低于80分为优秀,则本次决赛的优秀率是多少?
17.(2022春·贵州黔南·七年级统考期末)文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 年龄段 频数(人数)
第1组 5
第2组
第3组 35
第4组 20
第5组 15
(1)请直接写出 , ,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
18.(2022春·贵州黔西·七年级统考期末)在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额(单位:元),将数据分组如下:;;;;.,并将数据整理成如图所示的不完整统计图.已知,两组户数在频数分布直方图中的高度比为.
请根据以上信息,解答下列问题.
(1)组的频数是 ,本次调查的样本容量是 .
(2)补全频数分布直方图(需标明各组频数).
(3)所抽取的家庭中每月用于“信息消费”的金额不少于200元的有多少户?占所抽取家庭的百分之几?
19.(2022春·贵州黔南·七年级统考期末)某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设踢毽子;:篮球;:跳绳;:健美操四种运动项目.为了了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查(每个被调查的同学必须在以上体育活动中选择一种),并将调查结果绘制成如下两幅不完整统计图.请结合图中的信息解答下列问题:
(1)本次共调查了多少名学生?
(2)请补全条形统计图,并求出扇形统计图中C部分所对应的扇形圆心角的度数;
(3)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
参考答案:
1.D
【分析】根据具体情况正确选择普查或抽样调查方法,并理解有些调查是不适合使用普查方法的.要选择调查方式,需将普查的局限性和抽样调查的必要性结合起来具体分析.
【详解】要调查太原市中学生对垃圾分类知识的了解情况,就对所有学生进行一次全面的调查,费大量的人力物力是得不尝失的,采取抽样调查即可.考虑到抽样的全面性,所以应在在太原市所有中学生中随机抽取名学生进行调查;
故选:D.
【点睛】本题考查了抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.B
【分析】本题需要根据具体情况正确选择普查或抽样调查等方法,并理解有些调查是不适合使用普查方法的.要选择调查方式,需将普查的局限性和抽样调查的必要性结合起来具体分析.
【详解】解:要调查某区九年级8000名学生对“双减”政策的了解情况,就对所有学生进行一次全面的调查,费大量的人力物力是得不尝失的,采取抽样调查即可.考虑到抽样的全面性,
所以应在某区8000名九年级学生中随机选取800名学生.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.B
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】解:A.了解某市中学生视力情况,适合抽样调查,故本选项不符合题意;
B.第七次全国人口普查,适合全面调查,故本选项符合题意;
C.了解一批灯泡的使用寿命,适合抽样调查,故本选项不符合题意;
D.调查春节联欢晚会的收视率,适合抽样调查,故本选项不符合题意.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.B
【分析】根据个体的定义解答即可.
【详解】解:要了解七年级1500名学生的心理健康情况,从中抽取了300名学生的心理健康评估报告进行统计分析,其中“抽取的每名学生的心理健康评估报告”是个体.
故选:B.
【点睛】此题考查了调查中个体的定义:每个调查的对象称为个体,熟记定义是解题的关键.
5.D
【分析】利用折线统计图结合相应数据,分别分析得出符合题意的答案.
【详解】解:A、由折线统计图可得:与2015年相比,2016年我国与东欧地区的贸易额有所增长,正确,不合题意;
B、∵4554.4÷1368.2≈3.33,
∴2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多,
C、2011 2016年,我国与东南亚地区的贸易额的平均值为:
(3632.5+4003.0+4436.5+4803.6+4718.7+4554.4)÷6≈4358,
故超过4200亿美元,正确,不合题意,
D、由折线统计图可得:2011 2016年间,我国与东南亚地区的贸易额2014年后有所下降,故逐年增长错误,故此选项错误,符合题意;
故选:D.
【点睛】此题主要考查了折线统计图,利用折线统计图获取正确信息是解题关键.
6.B
【分析】求得极差,除以组距即可求得组数.
【详解】解:极差是:,
,则分成5组.
故选:B.
【点睛】本题考查了组数的计算,解题的关键是只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
7.D
【分析】观察频数分布直方图,找到横轴,代表次数,仰卧起坐次数在25~30次对应的纵轴人数是12人.
【详解】观察频数分布直方图,找到横轴,代表次数,
则仰卧起坐次数在25~30次对应的纵轴人数是12人.
故答案选:D.
【点睛】本题考查频数分布直方图.理解横轴和纵轴代表的意义是本题解题的关键.
8.400
【分析】根据样本容量的概念:一个样本中所包含的单位数,即可得出答案.
【详解】解:由题意,随机调查了其中400名学生,
所以样本容量为400.
故答案为:400
【点睛】本题考查样本容量的概念,理解样本容量的概念是解题的关键,注意样本容量不能带单位.
9.18
【分析】根据频率公式:频率即可求解.
【详解】解:(人,
所以该班级在这个分数段内的学生有18人.
故答案为:18.
【点睛】本题考查了频率的计算公式,解题的关键是掌握频率.
10.0.12
【分析】首先求出第五小组的频数,再求出频率即可.
【详解】解:第五组的频数为:50-18-10-12-4=6,
频率为,
故答案为:0.12.
【点睛】本题考查频数和频率,掌握频率公式是解决问题的关键,频率= .
11.(1)200;作图见解析;
(2)72;
(3)500,过程见解析.
【分析】(1)根据合格人数和已知百分比求出总人数即可解决问题,根据各分组人数之和等于总人数求出“合格”以及“优秀”的人数即可补全图形;
(2)根据圆心角=百分比计算即可;
(3)利用样本估算总体的思想解决问题即可.
(1)
本次抽取的样本容量为:,
故答案为:200.
测试为优秀的人数有:(人)
所以测试为合格的人数为:200-10-100-50=40(人)
补全频数分布直方图如图所示:
(2)
扇形统计图中“合格”等次所对应的圆心角n的值为:
故答案为:72.
(3)
(人)
答:估计该校2000名学生中获得“优秀”等次的学生有500人.
【点睛】本题考查频数分布直方图,样本估计总体,扇形统计图等知识,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
12.(1)图②, 图① (2)扇形统计图(略)
【分析】(1)图2用条形的高度表示各年级的总数,所以图2能更好地反映学校每个年级学生的总人数;图1分别表示了各年级男女的人数,所以图1能更好地比较学校每个年级男女生的人数;
(2)从2中得出七、八年级的总人数都为800人,九年级为300人,根据扇形所对圆心角的度数与百分比的关系是:圆心角的度数=百分比×360度计算相对应的圆心角.据此画出扇形统计图.
【详解】解:(1)图2能更好地反映学校每个年级学生的总人数.
图1能更好地比较学校每个年级男女生的人数.
(2)从2中得出七、八年级的总人数都为800人,九年级为300人,
∴总人数=800+800+300=1900,
七年级占总人数的比例=800÷1900=42.1%,
表示七年级的扇形的圆心角=42.1%×360°=151.56°,
八年级占总人数的比例=800÷1900=42.1%,
表示八年级的扇形的圆心角=42.1%×360°=151.56°,
九年级占总人数的比例=300÷1900=15.8%,
表示九年级的扇形的圆心角=15.8%×360°=56.88°.
【点睛】本题考查的是扇形统计图的制作,在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心的度数与360°的比.在制作统计图时,要注意写上统计图名称.
13.(1),,
(2)见解析
(3)
(4)240人
【分析】(1)由C组有18人,占比,可得样本总人数,再由频数分布直方图可得m,p的值,再由总人数减去各组频数可得n的值,
(2)由C组18人,D组8人,补全图形即可;
(3)由乘以D组的占比即可得到答案;
(4)由1000乘以D,E两组的占比即可得到答案.
(1)
解:由频数分布直方图可得:,
而总人数为(人),
∴
故答案为:,,.
(2)
由频数分布表可得组18人,而D组人数 补全图形如下:
(3)
扇形统计图中组的圆心角的度数为:.
(4)
成绩在90分以上(不含90分)的学生人数为:
(人).
【点睛】本题考查的是从条形图与扇形图中获取信息,补全条形图,求解扇形某部分所对的圆心角的大小,利用样本估计总体,掌握以上基础的统计知识是解本题的关键.
14.(1)200人
(2)见解析
(3)900人
【分析】(1)根据10~20分钟的有40人,所占的百分比是20%,据此即可求得调查的总人数;
(2)根据百分比的意义以及求得30~40分钟的人数所占的百分比,40~50分钟的人数所占的百分比以及20~30分钟所占的百分比和人数,从而补全统计图;
(3)利用总人数乘以对应的百分比即可.
(1)
调查的学生人数是:40÷20%=200(人),
故答案是:200;
(2)
30~40分钟的人数所占的百分比是:×100%=25%,
40~50分钟的人数所占的百分比是×100%=5%,
则20~30分钟所占的百分比是:1-25%-30%-20%-5%=20%,则人数是200×20%=40(人).
补全图形如下:
(3)
“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有3000×(25%+5%)=900(人).
学校要积极鼓励学生多做家务,学校要适当给予表扬.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
15.(1)200,16;(2)126°;(3)见解析;(4)846名
【分析】(1)根据B等级的频数和所占的百分比,可以求得样本容量,然后即可计算出a的值;
(2)根据频数分布直方图中的数据,可以计算出D等级对应扇形圆心角的度数;
(3)根据(1)中的结果和扇形统计图中的数据,可以计算出C等级的人数,然后即可将频数分布直方图补充完整;
(4)根据扇形统计图中的数据,可以计算出该校成绩优秀的学生约为多少名.
【详解】解:(1)样本容量为:40÷20%=200,
a=200×8%=16,
即样本容量为200,a的值是16;
(2)D等级对应扇形圆心角的度数为:360°×=126°,
即D等级对应扇形圆心角的度数为126°;
(3)C等级的人数为:200×25%=50,
补全的频数分布直方图如图所示;
(4)1800×(1﹣8%﹣20%﹣25%)=846(名),
即该校成绩优秀的学生约为846名.
【点睛】此题主要考查统计调查的应用,解题的关键是根据题意求出调查的总人数.
16.(1)12
(2)见解析
(3)44%
【分析】(1)用样本容量分别减去第1、2、3、5组的频数即可得到第4组的频数,即得到a的值;
(2)根据所求a的值即可补全频数分布直方图;
(3)由于测试成绩不低于80分为优秀,则第4、5组的人数为优秀,所以用第4、5组的频数和除以50即可得到本次测试的优秀率.
(1)
解:a=50 4 8 16 10=12;
(2)
频数分布直方图为:
(3)
×100%=44%,
答:本次测试的优秀率是44%.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
17.(1)25,20,126;(2)补全的频数分布直方图如图所示;见解析;(3)40~50岁年龄段的关注本次大会的人数约有60万人.
【分析】(1)随机选取总人数减去其他组人数即可得到a,第4组人数除以调查总人数即可得到答案;第3组人数所占百分比乘以360度,即可得到答案;
(2)由(1)值,有25人,即可得到答案;
(3)300万乘以调查40~50岁年龄段的百分比可得答案.
【详解】(1),
,
第3组人数在扇形统计图中所对应的圆心角是:,
故答案为25,20,126;
(2)由(1)值,有25人,
补全的频数分布直方图如图所示;
(3)(万人),
答:40~50岁年龄段的关注本次大会的人数约有60万人.
【点睛】本题考查扇形统计图和条形统计图,解题的关键是熟练读出扇形统计图和条形统计图的信息.
18.(1)2;50
(2)见解析
(3)所抽取的家庭中每月用于“信息消费”的金额不少于200元的有38户,占所抽取家庭的.
【分析】(1)由B组的频数为10,且A,B两组户数在频数分布直方图中的高度比为1:5可得A组频数;用A、B组频数和除以其所占百分比即可;
(2)用总人数分别乘以C、D、E对应的百分比得出其人数,从而补全图形;
(3)将C、D、E组人数相加得出不少于200元的户数,再将C、D、E组百分比相加得出其所占百分比即可.
(1)
由图知,组的频数为10,且,两组户数在频数分布直方图中的高度比为,
组的频数为2,
本次调查的样本容量为,
故答案为:2;50;
(2)
组频数为,组频数为,组频数为,
补全图形如下:
(3)
(户,,
答:所抽取的家庭中每月用于“信息消费”的金额不少于200元的有38户,占所抽取家庭的.
【点睛】本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
19.(1)200名;(2)图见解析,126°;(3)360名
【分析】(1)用踢毽子的人数除以它的百分比即可;
(2)求出篮球和健美操的人数画图即可;求出C部分所占百分比即可求出圆心角;
(3)用1200乘以喜欢篮球运动项目的百分比即可.
【详解】解:(1)人
答:本次共调查了200名学生.
(2)200×30%=60(人),所以为60人;
200-30-70-60=40(人),所以为40人;
补图如图所示,
,
圆心角度数为126°
(3)(名),
答:喜欢篮球运动项目的学生约有360名.
【点睛】本题考查了统计图,解题关键是准确从统计图中获得信息,熟练运用统计知识进行计算.
一、单选题
1.(2022春·贵州黔南·七年级统考期末)要调查太原市中学生对垃圾分类知识的了解情况,下列调查方式最适合的是( )
A.在太原市迎泽区某中学随机抽取名学生进行调查
B.在太原市所有中学男生中随机抽取名进行调查
C.在太原市所有中学初三年级中随机抽取名学生进行调查
D.在太原市所有中学生中随机抽取名学生进行调查
2.(2022春·贵州贵阳·七年级统考期末)要调查某区九年级 8000 名学生对“双减”政策的了解情况,下列调查方式最合适的是( )
A.在某校九年级学生中随机选取50名学生
B.在全区 8000 名九年级学生中随机选取800名学生
C.在全区 8000 名九年级学生中随机选取800名男生
D.在全区 8000 名九年级学生中随机选取800名女生
3.(2022春·贵州遵义·七年级统考期末)下列调查中,适合全面调查的是( )
A.了解某市中学生视力情况 B.第七次全国人口普查
C.了解一批灯泡的使用寿命 D.调查春节联欢晚会的收视率
4.(2022春·贵州黔西·七年级统考期末)要了解七年级1500名学生的心理健康情况,从中抽取了300名学生的心理健康评估报告进行统计分析,其中“抽取的每名学生的心理健康评估报告”是( )
A.总体 B.个体 C.样本 D.样本容量
5.(2022春·贵州贵阳·七年级统考期末)下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.
以上数据摘自《“一带一路”贸易合作大数据报告(2017)》,根据统计图提供的信息,下列推断不合理的是( )
A.与2015年相比,2016年我国与东欧地区的贸易额有所增长
B.2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多
C.2011-2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元
D.2011-2016年,我国与东南亚地区的贸易额逐年增长
6.(2022春·贵州遵义·七年级统考期末)已知数据35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34,在列频数分布表时,如果取组距为2,那么应分成组数为( )
A.4 B.5 C.6 D.7
7.(2022春·贵州黔南·七年级统考期末)某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图.那么仰卧起坐次数在25~30次的人数是( )
A.3人 B.5人 C.10人 D.12人
二、填空题
8.(2022春·贵州黔东南·七年级统考期末)为了解某地区七年级8460名学生中会游泳的学生人数,随机调查了其中400名学生,结果有150名学生会游泳,样本容量是 ________ .
9.(2022春·贵州黔南·七年级统考期末)某班级有45名学生参加了期中考试,分数段在70~79分的占比为40%,则该班级在这个分数段内的学生有_________人.
10.(2022春·贵州安顺·七年级统考期末)一次数学单元测试后,全班50名学生的成绩被分成5组,第1-4组的频数分别是18,10,12,4,则第五组的数率是___.
三、解答题
11.(2022春·贵州遵义·七年级统考期末)为了增强学生民主与法治意识,某校对2000名学生进行法治与安全相关知识测试随机抽取部分学生成绩进行分析,并将测试成绩分为四个等次:基本合格(),合格(),良好(),优秀(),并制作了下边不完整的统计图.
(1)本次抽取的样本容量为________,请补全频数分布直方图;
(2)扇形统计图中“合格”等次所对应的圆心角n的值为________;
(3)估计该校2000名学生中获得“优秀”等次的人数.
12.(2022春·贵州贵阳·七年级统考期末)图①、图②是李晓同学根据所在学校三个年级男女生人数画出的两幅条形图.
(1)两个图中哪个能更好地反映学校每个年级学生的总人数?哪个图能更好地比较每个年级男女生的人数?
(2)请按该校各年级学生人数在图③中画出扇形统计图.
13.(2022春·贵州黔东南·七年级统考期末)为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成如下不完整的统计图表:
组别 成绩(分) 频数
6
18
请你根据上面的统计图表提供的信息解答下列问题:
(1)上表中的_________,_________,_________.
(2)请补全频数分布直方图.
(3)计算扇形统计图中组的圆心角的度数.
(4)已知该校有1000名学生,请估计竞赛成绩在90分以上(不含90分)的学生有多少人?
14.(2022春·贵州黔东南·七年级统考期末)某学校为了解《大中小学劳动教育指导纲要(试行)》落实情况,就假期“平均每天帮助父母干家务所用时长”进行了调查,如图是根据相关数据绘制的统计图的一部分根据上述信息,回答下列问题:
(1)在本次随机抽取的样本中,调查的学生人数是多少?
(2)补全扇形统计图和频数分布直方图:
(3)如果该校共有学生3000人,请你估计“平均每天帮助父母干家务所用时长不少于30分钟”的学生大约有多少人?
15.(2022春·贵州遵义·七年级统考期末)为了加强学生的交通安全意识,遵义交利用微信公众号发布了交通安全知识在线测试从中抽取了部分学生在线测试成绩(分数取正整数,满分为100分)进行统计,绘制了下面不完整的频数分布直方图和扇形统计图,根据图中提供的信息解答下列问题:
(1)求样本容量和a的值;
(2)求D等级对应扇形圆心角的度数;
(3)补全频数分布直方图;
(4)若交通安全知识在线测试成绩在80分以上为优秀,某学校共有1800名学生,估计该校成绩优秀的学生约为多少名?
16.(2022春·贵州安顺·七年级统考期末)某县举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生被分为5组,同时听写100个汉字,每正确听写出一个汉字得1分.根据决赛成绩绘制出部分频数分布表和部分频数分布直方图如下.
组别 成绩x分 频数(人数)
第1组 4
第2组 8
第3组 16
第4组 a
第5组 10
根据以上信息,解决下列问题:
(1)频数分布表中a=________;
(2)请补全频数分布直方图.
(3)若决赛成绩不低于80分为优秀,则本次决赛的优秀率是多少?
17.(2022春·贵州黔南·七年级统考期末)文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 年龄段 频数(人数)
第1组 5
第2组
第3组 35
第4组 20
第5组 15
(1)请直接写出 , ,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
18.(2022春·贵州黔西·七年级统考期末)在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额(单位:元),将数据分组如下:;;;;.,并将数据整理成如图所示的不完整统计图.已知,两组户数在频数分布直方图中的高度比为.
请根据以上信息,解答下列问题.
(1)组的频数是 ,本次调查的样本容量是 .
(2)补全频数分布直方图(需标明各组频数).
(3)所抽取的家庭中每月用于“信息消费”的金额不少于200元的有多少户?占所抽取家庭的百分之几?
19.(2022春·贵州黔南·七年级统考期末)某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设踢毽子;:篮球;:跳绳;:健美操四种运动项目.为了了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查(每个被调查的同学必须在以上体育活动中选择一种),并将调查结果绘制成如下两幅不完整统计图.请结合图中的信息解答下列问题:
(1)本次共调查了多少名学生?
(2)请补全条形统计图,并求出扇形统计图中C部分所对应的扇形圆心角的度数;
(3)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
参考答案:
1.D
【分析】根据具体情况正确选择普查或抽样调查方法,并理解有些调查是不适合使用普查方法的.要选择调查方式,需将普查的局限性和抽样调查的必要性结合起来具体分析.
【详解】要调查太原市中学生对垃圾分类知识的了解情况,就对所有学生进行一次全面的调查,费大量的人力物力是得不尝失的,采取抽样调查即可.考虑到抽样的全面性,所以应在在太原市所有中学生中随机抽取名学生进行调查;
故选:D.
【点睛】本题考查了抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.B
【分析】本题需要根据具体情况正确选择普查或抽样调查等方法,并理解有些调查是不适合使用普查方法的.要选择调查方式,需将普查的局限性和抽样调查的必要性结合起来具体分析.
【详解】解:要调查某区九年级8000名学生对“双减”政策的了解情况,就对所有学生进行一次全面的调查,费大量的人力物力是得不尝失的,采取抽样调查即可.考虑到抽样的全面性,
所以应在某区8000名九年级学生中随机选取800名学生.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.B
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】解:A.了解某市中学生视力情况,适合抽样调查,故本选项不符合题意;
B.第七次全国人口普查,适合全面调查,故本选项符合题意;
C.了解一批灯泡的使用寿命,适合抽样调查,故本选项不符合题意;
D.调查春节联欢晚会的收视率,适合抽样调查,故本选项不符合题意.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.B
【分析】根据个体的定义解答即可.
【详解】解:要了解七年级1500名学生的心理健康情况,从中抽取了300名学生的心理健康评估报告进行统计分析,其中“抽取的每名学生的心理健康评估报告”是个体.
故选:B.
【点睛】此题考查了调查中个体的定义:每个调查的对象称为个体,熟记定义是解题的关键.
5.D
【分析】利用折线统计图结合相应数据,分别分析得出符合题意的答案.
【详解】解:A、由折线统计图可得:与2015年相比,2016年我国与东欧地区的贸易额有所增长,正确,不合题意;
B、∵4554.4÷1368.2≈3.33,
∴2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多,
C、2011 2016年,我国与东南亚地区的贸易额的平均值为:
(3632.5+4003.0+4436.5+4803.6+4718.7+4554.4)÷6≈4358,
故超过4200亿美元,正确,不合题意,
D、由折线统计图可得:2011 2016年间,我国与东南亚地区的贸易额2014年后有所下降,故逐年增长错误,故此选项错误,符合题意;
故选:D.
【点睛】此题主要考查了折线统计图,利用折线统计图获取正确信息是解题关键.
6.B
【分析】求得极差,除以组距即可求得组数.
【详解】解:极差是:,
,则分成5组.
故选:B.
【点睛】本题考查了组数的计算,解题的关键是只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
7.D
【分析】观察频数分布直方图,找到横轴,代表次数,仰卧起坐次数在25~30次对应的纵轴人数是12人.
【详解】观察频数分布直方图,找到横轴,代表次数,
则仰卧起坐次数在25~30次对应的纵轴人数是12人.
故答案选:D.
【点睛】本题考查频数分布直方图.理解横轴和纵轴代表的意义是本题解题的关键.
8.400
【分析】根据样本容量的概念:一个样本中所包含的单位数,即可得出答案.
【详解】解:由题意,随机调查了其中400名学生,
所以样本容量为400.
故答案为:400
【点睛】本题考查样本容量的概念,理解样本容量的概念是解题的关键,注意样本容量不能带单位.
9.18
【分析】根据频率公式:频率即可求解.
【详解】解:(人,
所以该班级在这个分数段内的学生有18人.
故答案为:18.
【点睛】本题考查了频率的计算公式,解题的关键是掌握频率.
10.0.12
【分析】首先求出第五小组的频数,再求出频率即可.
【详解】解:第五组的频数为:50-18-10-12-4=6,
频率为,
故答案为:0.12.
【点睛】本题考查频数和频率,掌握频率公式是解决问题的关键,频率= .
11.(1)200;作图见解析;
(2)72;
(3)500,过程见解析.
【分析】(1)根据合格人数和已知百分比求出总人数即可解决问题,根据各分组人数之和等于总人数求出“合格”以及“优秀”的人数即可补全图形;
(2)根据圆心角=百分比计算即可;
(3)利用样本估算总体的思想解决问题即可.
(1)
本次抽取的样本容量为:,
故答案为:200.
测试为优秀的人数有:(人)
所以测试为合格的人数为:200-10-100-50=40(人)
补全频数分布直方图如图所示:
(2)
扇形统计图中“合格”等次所对应的圆心角n的值为:
故答案为:72.
(3)
(人)
答:估计该校2000名学生中获得“优秀”等次的学生有500人.
【点睛】本题考查频数分布直方图,样本估计总体,扇形统计图等知识,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
12.(1)图②, 图① (2)扇形统计图(略)
【分析】(1)图2用条形的高度表示各年级的总数,所以图2能更好地反映学校每个年级学生的总人数;图1分别表示了各年级男女的人数,所以图1能更好地比较学校每个年级男女生的人数;
(2)从2中得出七、八年级的总人数都为800人,九年级为300人,根据扇形所对圆心角的度数与百分比的关系是:圆心角的度数=百分比×360度计算相对应的圆心角.据此画出扇形统计图.
【详解】解:(1)图2能更好地反映学校每个年级学生的总人数.
图1能更好地比较学校每个年级男女生的人数.
(2)从2中得出七、八年级的总人数都为800人,九年级为300人,
∴总人数=800+800+300=1900,
七年级占总人数的比例=800÷1900=42.1%,
表示七年级的扇形的圆心角=42.1%×360°=151.56°,
八年级占总人数的比例=800÷1900=42.1%,
表示八年级的扇形的圆心角=42.1%×360°=151.56°,
九年级占总人数的比例=300÷1900=15.8%,
表示九年级的扇形的圆心角=15.8%×360°=56.88°.
【点睛】本题考查的是扇形统计图的制作,在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心的度数与360°的比.在制作统计图时,要注意写上统计图名称.
13.(1),,
(2)见解析
(3)
(4)240人
【分析】(1)由C组有18人,占比,可得样本总人数,再由频数分布直方图可得m,p的值,再由总人数减去各组频数可得n的值,
(2)由C组18人,D组8人,补全图形即可;
(3)由乘以D组的占比即可得到答案;
(4)由1000乘以D,E两组的占比即可得到答案.
(1)
解:由频数分布直方图可得:,
而总人数为(人),
∴
故答案为:,,.
(2)
由频数分布表可得组18人,而D组人数 补全图形如下:
(3)
扇形统计图中组的圆心角的度数为:.
(4)
成绩在90分以上(不含90分)的学生人数为:
(人).
【点睛】本题考查的是从条形图与扇形图中获取信息,补全条形图,求解扇形某部分所对的圆心角的大小,利用样本估计总体,掌握以上基础的统计知识是解本题的关键.
14.(1)200人
(2)见解析
(3)900人
【分析】(1)根据10~20分钟的有40人,所占的百分比是20%,据此即可求得调查的总人数;
(2)根据百分比的意义以及求得30~40分钟的人数所占的百分比,40~50分钟的人数所占的百分比以及20~30分钟所占的百分比和人数,从而补全统计图;
(3)利用总人数乘以对应的百分比即可.
(1)
调查的学生人数是:40÷20%=200(人),
故答案是:200;
(2)
30~40分钟的人数所占的百分比是:×100%=25%,
40~50分钟的人数所占的百分比是×100%=5%,
则20~30分钟所占的百分比是:1-25%-30%-20%-5%=20%,则人数是200×20%=40(人).
补全图形如下:
(3)
“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有3000×(25%+5%)=900(人).
学校要积极鼓励学生多做家务,学校要适当给予表扬.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
15.(1)200,16;(2)126°;(3)见解析;(4)846名
【分析】(1)根据B等级的频数和所占的百分比,可以求得样本容量,然后即可计算出a的值;
(2)根据频数分布直方图中的数据,可以计算出D等级对应扇形圆心角的度数;
(3)根据(1)中的结果和扇形统计图中的数据,可以计算出C等级的人数,然后即可将频数分布直方图补充完整;
(4)根据扇形统计图中的数据,可以计算出该校成绩优秀的学生约为多少名.
【详解】解:(1)样本容量为:40÷20%=200,
a=200×8%=16,
即样本容量为200,a的值是16;
(2)D等级对应扇形圆心角的度数为:360°×=126°,
即D等级对应扇形圆心角的度数为126°;
(3)C等级的人数为:200×25%=50,
补全的频数分布直方图如图所示;
(4)1800×(1﹣8%﹣20%﹣25%)=846(名),
即该校成绩优秀的学生约为846名.
【点睛】此题主要考查统计调查的应用,解题的关键是根据题意求出调查的总人数.
16.(1)12
(2)见解析
(3)44%
【分析】(1)用样本容量分别减去第1、2、3、5组的频数即可得到第4组的频数,即得到a的值;
(2)根据所求a的值即可补全频数分布直方图;
(3)由于测试成绩不低于80分为优秀,则第4、5组的人数为优秀,所以用第4、5组的频数和除以50即可得到本次测试的优秀率.
(1)
解:a=50 4 8 16 10=12;
(2)
频数分布直方图为:
(3)
×100%=44%,
答:本次测试的优秀率是44%.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
17.(1)25,20,126;(2)补全的频数分布直方图如图所示;见解析;(3)40~50岁年龄段的关注本次大会的人数约有60万人.
【分析】(1)随机选取总人数减去其他组人数即可得到a,第4组人数除以调查总人数即可得到答案;第3组人数所占百分比乘以360度,即可得到答案;
(2)由(1)值,有25人,即可得到答案;
(3)300万乘以调查40~50岁年龄段的百分比可得答案.
【详解】(1),
,
第3组人数在扇形统计图中所对应的圆心角是:,
故答案为25,20,126;
(2)由(1)值,有25人,
补全的频数分布直方图如图所示;
(3)(万人),
答:40~50岁年龄段的关注本次大会的人数约有60万人.
【点睛】本题考查扇形统计图和条形统计图,解题的关键是熟练读出扇形统计图和条形统计图的信息.
18.(1)2;50
(2)见解析
(3)所抽取的家庭中每月用于“信息消费”的金额不少于200元的有38户,占所抽取家庭的.
【分析】(1)由B组的频数为10,且A,B两组户数在频数分布直方图中的高度比为1:5可得A组频数;用A、B组频数和除以其所占百分比即可;
(2)用总人数分别乘以C、D、E对应的百分比得出其人数,从而补全图形;
(3)将C、D、E组人数相加得出不少于200元的户数,再将C、D、E组百分比相加得出其所占百分比即可.
(1)
由图知,组的频数为10,且,两组户数在频数分布直方图中的高度比为,
组的频数为2,
本次调查的样本容量为,
故答案为:2;50;
(2)
组频数为,组频数为,组频数为,
补全图形如下:
(3)
(户,,
答:所抽取的家庭中每月用于“信息消费”的金额不少于200元的有38户,占所抽取家庭的.
【点睛】本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
19.(1)200名;(2)图见解析,126°;(3)360名
【分析】(1)用踢毽子的人数除以它的百分比即可;
(2)求出篮球和健美操的人数画图即可;求出C部分所占百分比即可求出圆心角;
(3)用1200乘以喜欢篮球运动项目的百分比即可.
【详解】解:(1)人
答:本次共调查了200名学生.
(2)200×30%=60(人),所以为60人;
200-30-70-60=40(人),所以为40人;
补图如图所示,
,
圆心角度数为126°
(3)(名),
答:喜欢篮球运动项目的学生约有360名.
【点睛】本题考查了统计图,解题关键是准确从统计图中获得信息,熟练运用统计知识进行计算.
