第十八章平行四边形专题复习之变化中的正方形
文档属性
| 名称 | 第十八章平行四边形专题复习之变化中的正方形 |
|
|
| 格式 | zip | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-04 00:00:00 | ||
图片预览

文档简介
课题 第十八章平行四边形专题复习之变化中的正方形
授课日期 2014年4月 22日 授课班级 八年一班
课型 专题复习课 教者姓名 王 波
教学目标 知识与技能:通过正方形的变化,让学生经历规律再现过程,引导学生发现变化图形中的线段有怎样的关系,巩固四边形的知识及全等的证明方法。
过程与方法:形成解决图形的基本策略,学会解题方法的迁移。
情感态度、价值观:积极参与到探究活动中,独立思考,获得成功体验;建立自信,感受变化中的和谐美。
设计意图 正方形是四边形中最特殊的一种图形,通过本 ( http: / / www.21cnjy.com )章的学习,我们的学生已然可以尝试着解决中考26的变式题。为了让学生感受“图变法不变”的解题原理,体会从特殊到一般的数学思想,我以正方形为背景设计了两组探究题组。
重点 探究变化中的正方形的证明方法。
难点 能将研究的方法迁移,解决运动图形中的数量关系。
教学流程
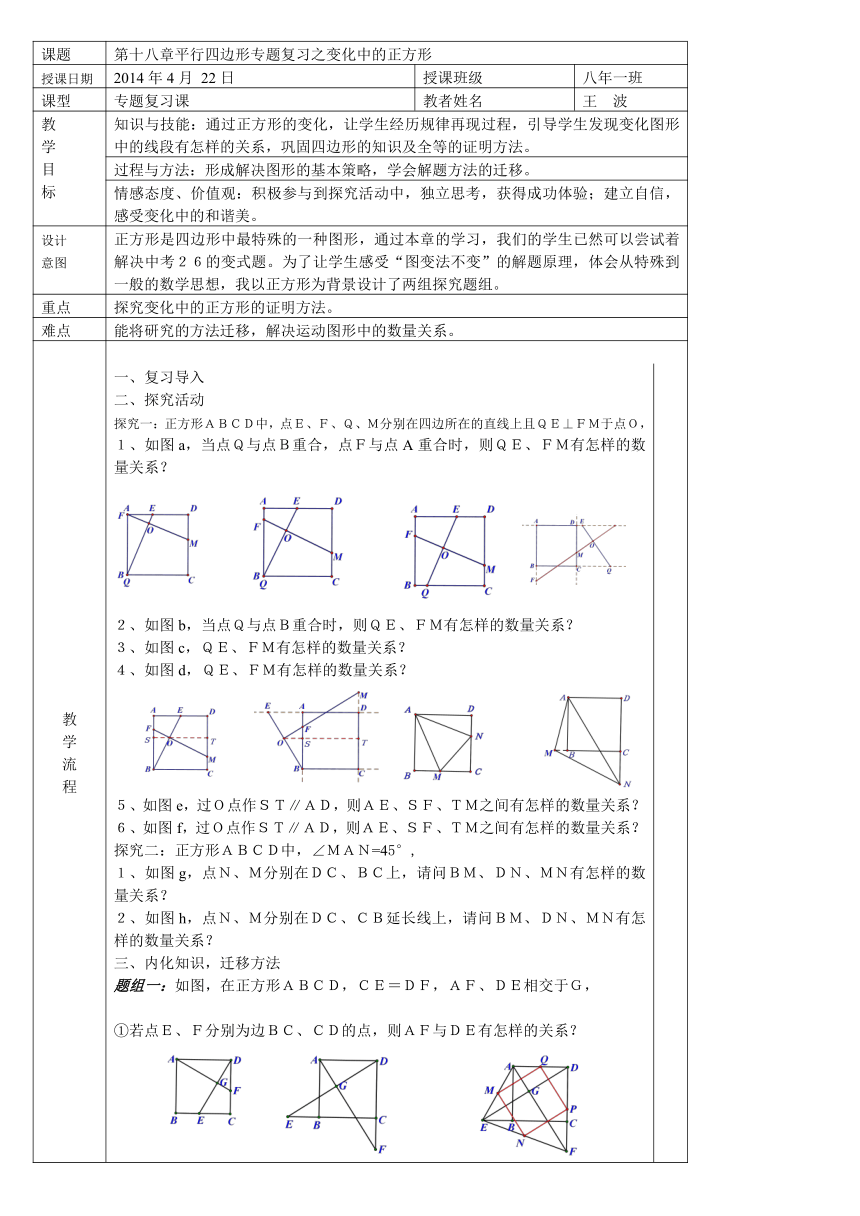
一、复习导入二、探究活动探究一:正方形ABCD中,点E、F、Q、M分别在四边所在的直线上且QE⊥FM于点O,1、如图a,当点Q与点B重合,点F与点A重合时,则QE、FM有怎样的数量关系?2、如图b,当点Q与点B重合时,则QE、FM有怎样的数量关系?3、如图c,QE、FM有怎样的数量关系?4、如图d,QE、FM有怎样的数量关系?5、如图e,过O点作ST∥AD,则AE、SF、TM之间有怎样的数量关系?6、如图f,过O点作ST∥AD,则AE、SF、TM之间有怎样的数量关系?探究二:正方形ABCD中,∠MAN=45°,1、如图g,点N、M分别在DC、BC上,请问BM、DN、MN有怎样的数量关系?2、如图h,点N、M分别在DC、CB延长线上,请问BM、DN、MN有怎样的数量关系?三、内化知识,迁移方法题组一:如图,在正方形ABCD,CE=DF,AF、DE相交于G,①若点E、F分别为边BC、CD的点,则AF与DE有怎样的关系? ②如图,点E、F分别为边CB、DC边延长线上的点,上面结论成立吗?③如图,若在上图的基础上,连AE、EF,取AE、EF、FD、DA中点M、N、P、Q,试判断四边形MNPQ的形状?说明理由?题组二:如图,在分别为正三角形ABC,正四边形ABCM,正五边形ABCMN中,BE=CD,BD交AE于点P。则图1中∠APD=__________;图2中∠APD=__________;图3中∠APD=__________.根据前面的探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论?若不能,说明理由。四、课堂小结五、布置作业
授课日期 2014年4月 22日 授课班级 八年一班
课型 专题复习课 教者姓名 王 波
教学目标 知识与技能:通过正方形的变化,让学生经历规律再现过程,引导学生发现变化图形中的线段有怎样的关系,巩固四边形的知识及全等的证明方法。
过程与方法:形成解决图形的基本策略,学会解题方法的迁移。
情感态度、价值观:积极参与到探究活动中,独立思考,获得成功体验;建立自信,感受变化中的和谐美。
设计意图 正方形是四边形中最特殊的一种图形,通过本 ( http: / / www.21cnjy.com )章的学习,我们的学生已然可以尝试着解决中考26的变式题。为了让学生感受“图变法不变”的解题原理,体会从特殊到一般的数学思想,我以正方形为背景设计了两组探究题组。
重点 探究变化中的正方形的证明方法。
难点 能将研究的方法迁移,解决运动图形中的数量关系。
教学流程
一、复习导入二、探究活动探究一:正方形ABCD中,点E、F、Q、M分别在四边所在的直线上且QE⊥FM于点O,1、如图a,当点Q与点B重合,点F与点A重合时,则QE、FM有怎样的数量关系?2、如图b,当点Q与点B重合时,则QE、FM有怎样的数量关系?3、如图c,QE、FM有怎样的数量关系?4、如图d,QE、FM有怎样的数量关系?5、如图e,过O点作ST∥AD,则AE、SF、TM之间有怎样的数量关系?6、如图f,过O点作ST∥AD,则AE、SF、TM之间有怎样的数量关系?探究二:正方形ABCD中,∠MAN=45°,1、如图g,点N、M分别在DC、BC上,请问BM、DN、MN有怎样的数量关系?2、如图h,点N、M分别在DC、CB延长线上,请问BM、DN、MN有怎样的数量关系?三、内化知识,迁移方法题组一:如图,在正方形ABCD,CE=DF,AF、DE相交于G,①若点E、F分别为边BC、CD的点,则AF与DE有怎样的关系? ②如图,点E、F分别为边CB、DC边延长线上的点,上面结论成立吗?③如图,若在上图的基础上,连AE、EF,取AE、EF、FD、DA中点M、N、P、Q,试判断四边形MNPQ的形状?说明理由?题组二:如图,在分别为正三角形ABC,正四边形ABCM,正五边形ABCMN中,BE=CD,BD交AE于点P。则图1中∠APD=__________;图2中∠APD=__________;图3中∠APD=__________.根据前面的探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论?若不能,说明理由。四、课堂小结五、布置作业
