陕西省西安市高新一中2014届高三下学期第十一次大练习数学(文)试题
文档属性
| 名称 | 陕西省西安市高新一中2014届高三下学期第十一次大练习数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 416.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-04 19:10:37 | ||
图片预览




文档简介
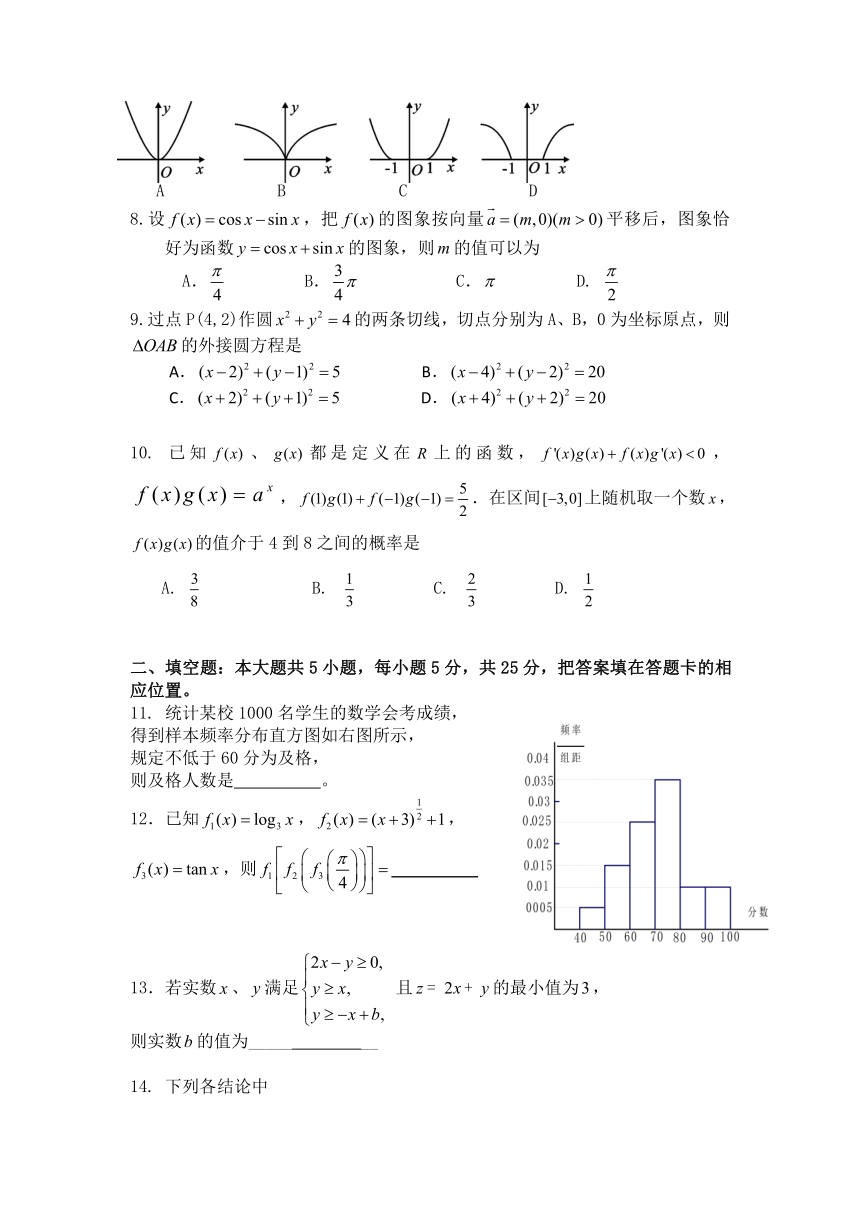
2014届第十一次大练习数学试题(文)
1.复数满足,则复数的实部与虚部之差为
A. B. C. D.
2.已知集合,,则等于
A.(-∞,5) B.(-∞,2) C. (1,2) D.
3. 执行右边的程序框图,若输出的是,,
则判断框内的应是
A.
B.
C.
D.
4.如图是一个几何体的三视图,该几何体的体积是
A.
B.
C.
D.
5. 已知数列的前项和为,且,则等于
A. B. 1 C. 2 D. 4
6. 的值为
A. B. C. D.
7. 函数的大致图像是
A B C D
8.设,把的图象按向量平移后,图象恰好为函数的图象,则的值可以为
A. B. C. D.
9.过点P(4,2)作圆的两条切线,切点分别为A、B,0为坐标原点,则的外接圆方程是
A. B.
C. D.
10. 已知、都是定义在上的函数,,,.在区间上随机取一个数,的值介于4到8之间的概率是
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
11. 统计某校1000名学生的数学会考成绩,
得到样本频率分布直方图如右图所示,
规定不低于60分为及格,
则及格人数是 。
12.已知,,
,则
13.若实数、满足 且的最小值为,
则实数的值为_____ __
14. 下列各结论中
①抛物线的焦点到直线的距离为
②已知函数的图象经过点,则的值等于
③命题“存在,”的否定是“对于任意,
正确结论的序号是
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
.设函数。则不等式的解集为 ;
.(坐标系与参数方程选做题)曲线:(为参数),若以点为极点,轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
。(几何证明选讲选做题) 如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,弧,交于,且,则_______
三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题12分)
已知数列满足,,等比数列的首项为2,公比为。
(Ⅰ)若,问等于数列中的第几项?
(Ⅱ)数列和的前项和分别记为和,的最大值为,当时,试比较与的大小
17.(本小题12分)
已知中,角、、的对边分别为、、,
角不是最大角,,外接圆的圆心为,半径为。
(Ⅰ)求的值;
(Ⅱ)若,求的周长
18.(本小题满分12分)
在某次高三大练习考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:(选择题满分分,填空题满分分。)
选择题
40
55
50
45
50
40
45
60
40
填空题
12
16
12
16
12
8
12
8
(Ⅰ)若这九位同学填空题得分的平均分为,试求表中的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为,填空题得分组成的集合为.若同学甲的解答题的得分是,现分别从集合、中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于分的概率
19.(本小题满分12分)
如图,为圆的直径,点、在圆上,,矩形所在的平面
和圆所在的平面互相垂直,且,.
(Ⅰ)求证:平面;
(Ⅱ)设的中点为,求证:平面;
(Ⅲ)设平面将几何体分成的两个锥体的体积分别为,
,求.
20.(本小题满分13分)
已知为实数,是函数的一个极值点。
(Ⅰ)若函数在区间上单调递减,求实数的取值范围;
(Ⅱ)设函数,对于任意和,有不等式恒成立,求实数的取值范围
21.(本小题满分14分)
已知椭圆的离心率为,直线与以原点为圆心、椭圆的短半轴长为半径的圆相切。
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左焦点为,右焦点为,直线过点,且垂直于椭圆的长轴,动直线垂直于,垂足为点,线段的垂直平分线交于点,求点的轨迹的方程;
(Ⅲ)过椭圆的左顶点做直线,与圆相交于两点、,若是钝角三角形,求直线的斜率的取值范围。
2014届第十一次大练习数学试题(文)
答案及评细则分
1.复数满足,则复数的实部与虚部之差为 答案D
A. B. C. D.
2.已知集合,,则等于 答案C
A.(-∞,5) B.(-∞,2) C. (1,2) D.
3. 执行右边的程序框图,若输出的是,
则判断框内的应是 答案C
A.
B.
C.
D.
4.如图是一个几何体的三视图,该几何体的体积是 答案B
A.
B.
C.
D.
5. 已知数列的前项和为,且,则等于 答案D.
A. B. 1 C. 2 D. 4
6. 的值为 答案C.
A. B. C. D.
7. 函数的大致图像是 答案B
A B C D
8.设,把的图象按向量平移后,图象恰好为函数的图象,则的值可以为 答案 D
A. B. C. D.
9.过点P(4,2)作圆的两条切线,切点分别为A、B,0为坐标原点,则的外接圆方程是 答案 A
A. B.
C. D.
10. 已知、都是定义在上的函数,,,.在区间上随机取一个数,的值介于4到8之间的概率是 答案B
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
11. 统计某校1000名学生的数学会考成绩,
得到样本频率分布直方图如右图所示,
规定不低于60分为及格,
则及格人数是 。
答案
12.已知,,
,则
答案
13.若实数、满足 且的最小值为,
则实数的值为_____ __ 答案
14. 下列各结论中
①抛物线的焦点到直线的距离为
②已知函数的图象经过点,则的值等于
③命题“存在,”的否定是“对于任意,
正确结论的序号是
答案①②
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
.设函数。则不等式的解集为 ;
答案
.(坐标系与参数方程选做题)曲线:(为参数),若以点为极点,轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
答案
。(几何证明选讲选做题) 如图,⊙的直径的延长线
与弦的延长线相交于点,为⊙上一点,弧
,交于,且,则
_______
答案
三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题12分)
已知数列满足,,等比数列的首项为2,公比为。
(Ⅰ)若,问等于数列中的第几项?
(Ⅱ)数列和的前项和分别记为和,的最大值为,当时,试比较与的大小
解:(I). ……………2分
由,得,即是公差的等差数列.……………3分
由,得.
. ………………5分
令,得.
等于数列中的第项. ………………6分
(Ⅱ),. …………8分
又,
. ……………11分
. ……………12分
17.(本小题12分)
已知中,角、、的对边分别为、、,
角不是最大角,,外接圆的圆心为,半径为。
(Ⅰ)求的值;
(Ⅱ)若,求的周长
17.解:(I)由正弦定理,得
.
或. ……………2分
又不是最大角,
.
. ……………4分
.
. ……………6分
(注:)
(Ⅱ). ……………8分
由余弦定理,得
.
周长为. ……………12分
18.(本小题满分12分)
在某次高三大练习考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:(选择题满分分,填空题满分分。)
选择题
40
55
50
45
50
40
45
60
40
填空题
12
16
12
16
12
8
12
8
(Ⅰ)若这九位同学填空题得分的平均分为,试求表中的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为,填空题得分组成的集合为.若同学甲的解答题的得分是,现分别从集合、中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于分的概率
解:(I)由填空题得分的平均分为,可得……………2分
填空题得分的标准差
. ……………………………4分
(Ⅱ),,,,,,,.……………………6分
分别从集合、中各任取一个值当作其选择题和填空题的得分,得分之和共有下列15个值:
48,53,58,63,68,52,57,62,67,72,56,61,66,71,76.………9分
当同学甲的解答题的得分是分时,其选择题和填空题的得分之和要大于54分,其数学成绩成绩才高于100分,
又选择题和填空题的得分之和要大于54分的共个值,
所求概率是. ……………12分
19.(本小题满分12分)
如图,为圆的直径,点、在圆上,,矩形所在的平面
和圆所在的平面互相垂直,且,.
(Ⅰ)求证:平面;
(Ⅱ)设的中点为,求证:平面;
(Ⅲ)设平面将几何体分成的两个锥体的体积分别为,
,求.
19.(Ⅰ)证明: 平面平面,,
平面平面=,平面,
平面, ,又为圆的直径,,
平面。 ………………4分
(Ⅱ)设的中点为,则,又,
则,为平行四边形,,又平面,平面,平面。 ………………8分
(Ⅲ)过点作于,平面平面,
平面,, 平面,
,. ………………12分
20.(本小题13分)
已知为实数,是函数的一个极值点。
(Ⅰ)若函数在区间上单调递减,求实数的取值范围;
(Ⅱ)设函数,对于任意和,有不等式恒成立,求实数的取值范围
20.解: ……………1分
(Ⅰ). …………3分
首先.
得.
令,得即的单调递减区间是. …………5分
在区间上单调递减,
. ……………7分
(Ⅱ)由(I),,列表如下:
0
0
↗
极大值
↘
极小值
↗
则,. …………9分
.
恒成立恒成立. …………11分
,当且仅当时取等号,
或. ………………13分
21.(本小题满分14分)
已知椭圆的离心率为,直线与以原点为圆心、椭圆的短半轴长为半径的圆相切。
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左焦点为,右焦点为,直线过点,且垂直于椭圆的长轴,动直线垂直于,垂足为点,线段的垂直平分线交于点,求点的轨迹的方程;
(Ⅲ)过椭圆的左顶点做直线,与圆相交于两点、,若是钝角三角形,求直线的斜率的取值范围。
21.解:(Ⅰ)由 ………………2分
由直线
所以椭圆的方程是 …………………4分
(Ⅱ)由条件,知|MF2|=|MP|。即动点M到定点F2的距离等于它到直线的距离,由抛物线的定义得点M的轨迹C2的方程是。 …………8分
(Ⅲ)由(1),得圆O的方程是
设
得
则 ……………9分
由 ①…………10分
因为
所以 ②……12分
由A、R、S三点不共线,知。 ③
由①、②、③,得直线m的斜率k的取值范围是……14分
(注:其它解法相应给分)
1.复数满足,则复数的实部与虚部之差为
A. B. C. D.
2.已知集合,,则等于
A.(-∞,5) B.(-∞,2) C. (1,2) D.
3. 执行右边的程序框图,若输出的是,,
则判断框内的应是
A.
B.
C.
D.
4.如图是一个几何体的三视图,该几何体的体积是
A.
B.
C.
D.
5. 已知数列的前项和为,且,则等于
A. B. 1 C. 2 D. 4
6. 的值为
A. B. C. D.
7. 函数的大致图像是
A B C D
8.设,把的图象按向量平移后,图象恰好为函数的图象,则的值可以为
A. B. C. D.
9.过点P(4,2)作圆的两条切线,切点分别为A、B,0为坐标原点,则的外接圆方程是
A. B.
C. D.
10. 已知、都是定义在上的函数,,,.在区间上随机取一个数,的值介于4到8之间的概率是
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
11. 统计某校1000名学生的数学会考成绩,
得到样本频率分布直方图如右图所示,
规定不低于60分为及格,
则及格人数是 。
12.已知,,
,则
13.若实数、满足 且的最小值为,
则实数的值为_____ __
14. 下列各结论中
①抛物线的焦点到直线的距离为
②已知函数的图象经过点,则的值等于
③命题“存在,”的否定是“对于任意,
正确结论的序号是
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
.设函数。则不等式的解集为 ;
.(坐标系与参数方程选做题)曲线:(为参数),若以点为极点,轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
。(几何证明选讲选做题) 如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,弧,交于,且,则_______
三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题12分)
已知数列满足,,等比数列的首项为2,公比为。
(Ⅰ)若,问等于数列中的第几项?
(Ⅱ)数列和的前项和分别记为和,的最大值为,当时,试比较与的大小
17.(本小题12分)
已知中,角、、的对边分别为、、,
角不是最大角,,外接圆的圆心为,半径为。
(Ⅰ)求的值;
(Ⅱ)若,求的周长
18.(本小题满分12分)
在某次高三大练习考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:(选择题满分分,填空题满分分。)
选择题
40
55
50
45
50
40
45
60
40
填空题
12
16
12
16
12
8
12
8
(Ⅰ)若这九位同学填空题得分的平均分为,试求表中的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为,填空题得分组成的集合为.若同学甲的解答题的得分是,现分别从集合、中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于分的概率
19.(本小题满分12分)
如图,为圆的直径,点、在圆上,,矩形所在的平面
和圆所在的平面互相垂直,且,.
(Ⅰ)求证:平面;
(Ⅱ)设的中点为,求证:平面;
(Ⅲ)设平面将几何体分成的两个锥体的体积分别为,
,求.
20.(本小题满分13分)
已知为实数,是函数的一个极值点。
(Ⅰ)若函数在区间上单调递减,求实数的取值范围;
(Ⅱ)设函数,对于任意和,有不等式恒成立,求实数的取值范围
21.(本小题满分14分)
已知椭圆的离心率为,直线与以原点为圆心、椭圆的短半轴长为半径的圆相切。
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左焦点为,右焦点为,直线过点,且垂直于椭圆的长轴,动直线垂直于,垂足为点,线段的垂直平分线交于点,求点的轨迹的方程;
(Ⅲ)过椭圆的左顶点做直线,与圆相交于两点、,若是钝角三角形,求直线的斜率的取值范围。
2014届第十一次大练习数学试题(文)
答案及评细则分
1.复数满足,则复数的实部与虚部之差为 答案D
A. B. C. D.
2.已知集合,,则等于 答案C
A.(-∞,5) B.(-∞,2) C. (1,2) D.
3. 执行右边的程序框图,若输出的是,
则判断框内的应是 答案C
A.
B.
C.
D.
4.如图是一个几何体的三视图,该几何体的体积是 答案B
A.
B.
C.
D.
5. 已知数列的前项和为,且,则等于 答案D.
A. B. 1 C. 2 D. 4
6. 的值为 答案C.
A. B. C. D.
7. 函数的大致图像是 答案B
A B C D
8.设,把的图象按向量平移后,图象恰好为函数的图象,则的值可以为 答案 D
A. B. C. D.
9.过点P(4,2)作圆的两条切线,切点分别为A、B,0为坐标原点,则的外接圆方程是 答案 A
A. B.
C. D.
10. 已知、都是定义在上的函数,,,.在区间上随机取一个数,的值介于4到8之间的概率是 答案B
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
11. 统计某校1000名学生的数学会考成绩,
得到样本频率分布直方图如右图所示,
规定不低于60分为及格,
则及格人数是 。
答案
12.已知,,
,则
答案
13.若实数、满足 且的最小值为,
则实数的值为_____ __ 答案
14. 下列各结论中
①抛物线的焦点到直线的距离为
②已知函数的图象经过点,则的值等于
③命题“存在,”的否定是“对于任意,
正确结论的序号是
答案①②
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
.设函数。则不等式的解集为 ;
答案
.(坐标系与参数方程选做题)曲线:(为参数),若以点为极点,轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
答案
。(几何证明选讲选做题) 如图,⊙的直径的延长线
与弦的延长线相交于点,为⊙上一点,弧
,交于,且,则
_______
答案
三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题12分)
已知数列满足,,等比数列的首项为2,公比为。
(Ⅰ)若,问等于数列中的第几项?
(Ⅱ)数列和的前项和分别记为和,的最大值为,当时,试比较与的大小
解:(I). ……………2分
由,得,即是公差的等差数列.……………3分
由,得.
. ………………5分
令,得.
等于数列中的第项. ………………6分
(Ⅱ),. …………8分
又,
. ……………11分
. ……………12分
17.(本小题12分)
已知中,角、、的对边分别为、、,
角不是最大角,,外接圆的圆心为,半径为。
(Ⅰ)求的值;
(Ⅱ)若,求的周长
17.解:(I)由正弦定理,得
.
或. ……………2分
又不是最大角,
.
. ……………4分
.
. ……………6分
(注:)
(Ⅱ). ……………8分
由余弦定理,得
.
周长为. ……………12分
18.(本小题满分12分)
在某次高三大练习考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:(选择题满分分,填空题满分分。)
选择题
40
55
50
45
50
40
45
60
40
填空题
12
16
12
16
12
8
12
8
(Ⅰ)若这九位同学填空题得分的平均分为,试求表中的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为,填空题得分组成的集合为.若同学甲的解答题的得分是,现分别从集合、中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于分的概率
解:(I)由填空题得分的平均分为,可得……………2分
填空题得分的标准差
. ……………………………4分
(Ⅱ),,,,,,,.……………………6分
分别从集合、中各任取一个值当作其选择题和填空题的得分,得分之和共有下列15个值:
48,53,58,63,68,52,57,62,67,72,56,61,66,71,76.………9分
当同学甲的解答题的得分是分时,其选择题和填空题的得分之和要大于54分,其数学成绩成绩才高于100分,
又选择题和填空题的得分之和要大于54分的共个值,
所求概率是. ……………12分
19.(本小题满分12分)
如图,为圆的直径,点、在圆上,,矩形所在的平面
和圆所在的平面互相垂直,且,.
(Ⅰ)求证:平面;
(Ⅱ)设的中点为,求证:平面;
(Ⅲ)设平面将几何体分成的两个锥体的体积分别为,
,求.
19.(Ⅰ)证明: 平面平面,,
平面平面=,平面,
平面, ,又为圆的直径,,
平面。 ………………4分
(Ⅱ)设的中点为,则,又,
则,为平行四边形,,又平面,平面,平面。 ………………8分
(Ⅲ)过点作于,平面平面,
平面,, 平面,
,. ………………12分
20.(本小题13分)
已知为实数,是函数的一个极值点。
(Ⅰ)若函数在区间上单调递减,求实数的取值范围;
(Ⅱ)设函数,对于任意和,有不等式恒成立,求实数的取值范围
20.解: ……………1分
(Ⅰ). …………3分
首先.
得.
令,得即的单调递减区间是. …………5分
在区间上单调递减,
. ……………7分
(Ⅱ)由(I),,列表如下:
0
0
↗
极大值
↘
极小值
↗
则,. …………9分
.
恒成立恒成立. …………11分
,当且仅当时取等号,
或. ………………13分
21.(本小题满分14分)
已知椭圆的离心率为,直线与以原点为圆心、椭圆的短半轴长为半径的圆相切。
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左焦点为,右焦点为,直线过点,且垂直于椭圆的长轴,动直线垂直于,垂足为点,线段的垂直平分线交于点,求点的轨迹的方程;
(Ⅲ)过椭圆的左顶点做直线,与圆相交于两点、,若是钝角三角形,求直线的斜率的取值范围。
21.解:(Ⅰ)由 ………………2分
由直线
所以椭圆的方程是 …………………4分
(Ⅱ)由条件,知|MF2|=|MP|。即动点M到定点F2的距离等于它到直线的距离,由抛物线的定义得点M的轨迹C2的方程是。 …………8分
(Ⅲ)由(1),得圆O的方程是
设
得
则 ……………9分
由 ①…………10分
因为
所以 ②……12分
由A、R、S三点不共线,知。 ③
由①、②、③,得直线m的斜率k的取值范围是……14分
(注:其它解法相应给分)
同课章节目录
