人教版七年5.1.3同位角内错角同旁内角 公开课课件(共24张PPT)
文档属性
| 名称 | 人教版七年5.1.3同位角内错角同旁内角 公开课课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 12:58:52 | ||
图片预览


文档简介
(共24张PPT)
数学 人教版 七年级下册
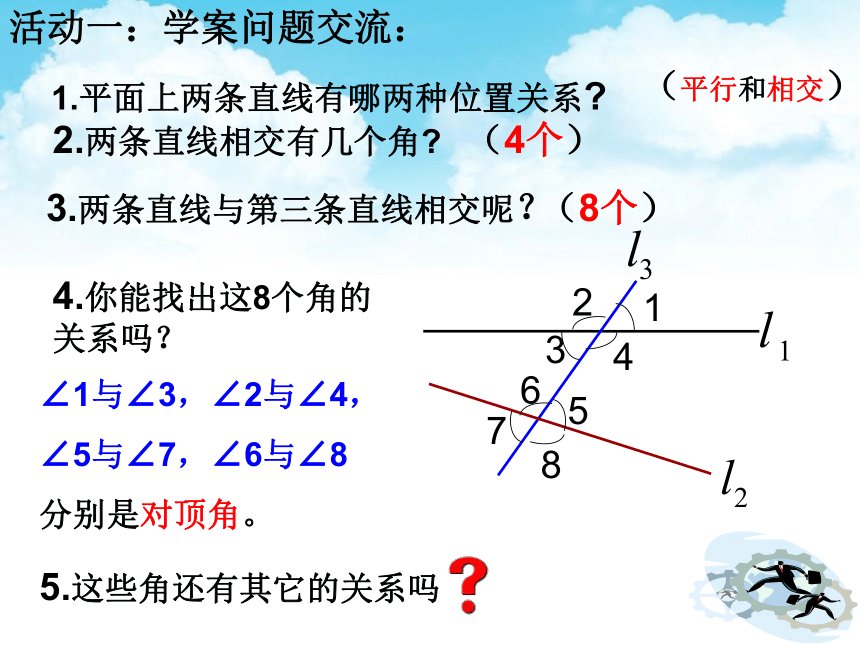
活动一:学案问题交流:
1.平面上两条直线有哪两种位置关系
(平行和相交)
1
2
3
4
5
6
7
8
2.两条直线相交有几个角
(4个)
3.两条直线与第三条直线相交呢?
(8个)
4.你能找出这8个角的关系吗?
∠1与∠3,∠2与∠4,
∠5与∠7,∠6与∠8
分别是对顶角。
5.这些角还有其它的关系吗
A
C
B
D
E
F
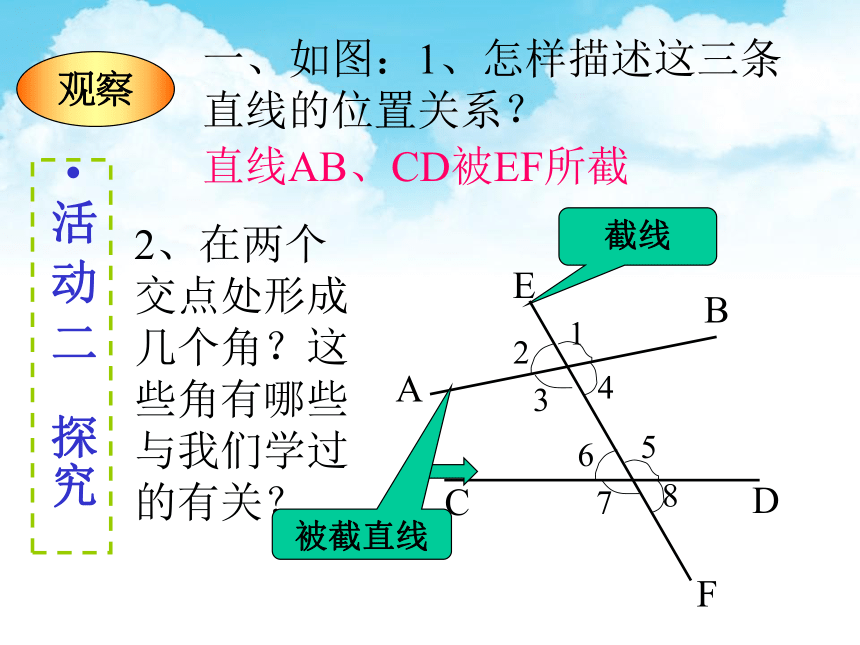
一、如图:1、怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
2、在两个交点处形成几个角?这些角有哪些与我们学过的有关?
7
1
2
3
4
5
6
8
观察
截线
被截直线
活 动 二 探究
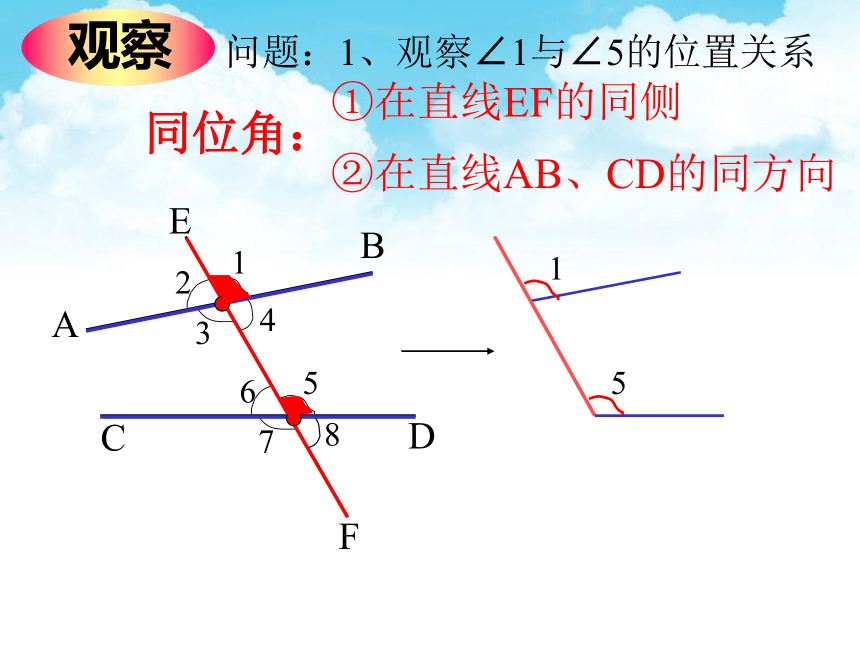
观察
F
问题:1、观察∠1与∠5的位置关系
①在直线EF的同侧
②在直线AB、CD的同方向
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
同位角:
2.图中还有其它的同位角吗?若有,请你找出来.
F
1
2
3
4
5
6
7
8
D
C
A
B
E
①
5
1
②
6
2
③
3
7
同位角是 F 形状
8
4
④
A
C
B
D
E
F
1
2
3
4
5
6
7
8
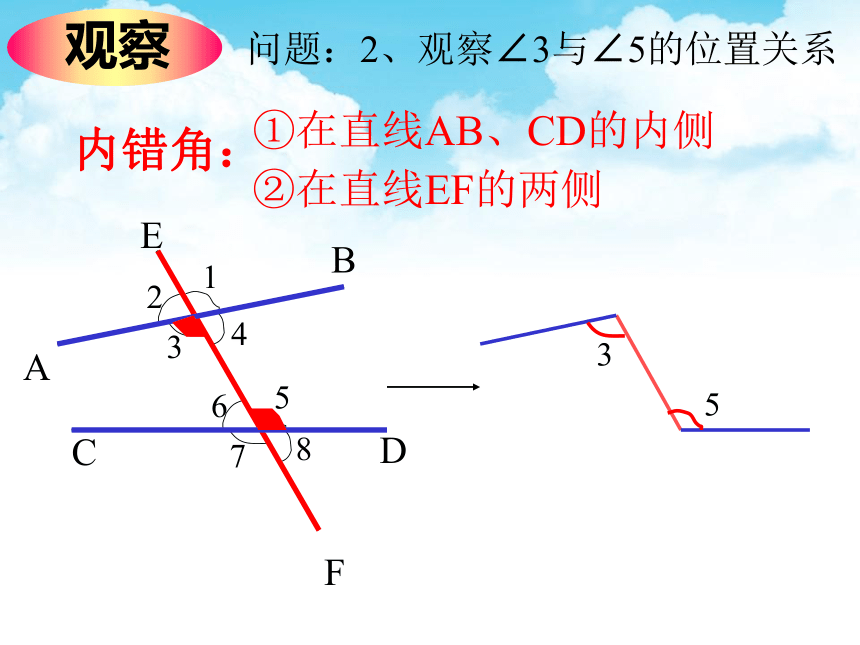
观察
问题:2、观察∠3与∠5的位置关系
①在直线AB、CD的内侧
②在直线EF的两侧
3
5
内错角:
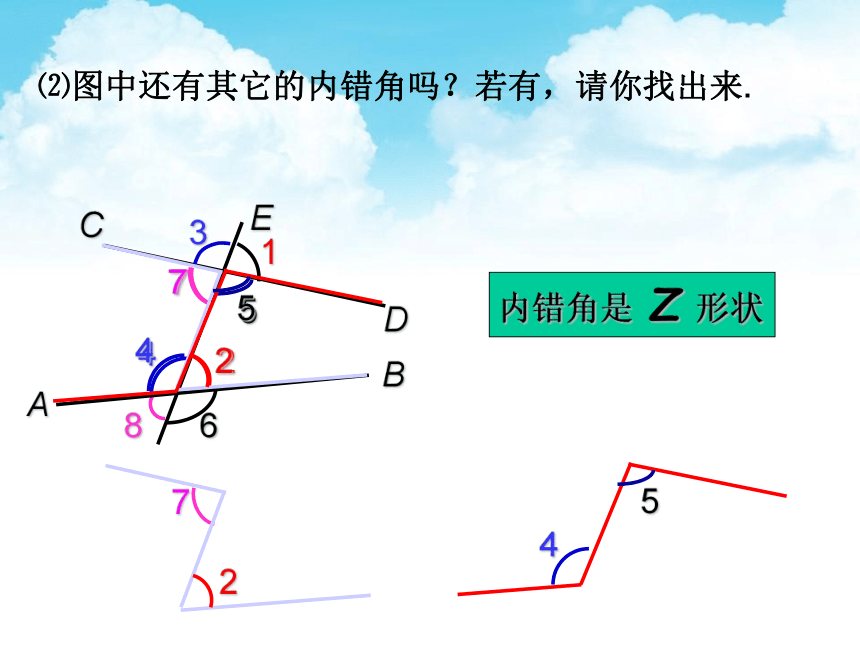
⑵图中还有其它的内错角吗?若有,请你找出来.
1
3
7
5
2
4
8
6
D
C
A
B
E
7
2
5
4
7
2
5
4
内错角是 Z 形状
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
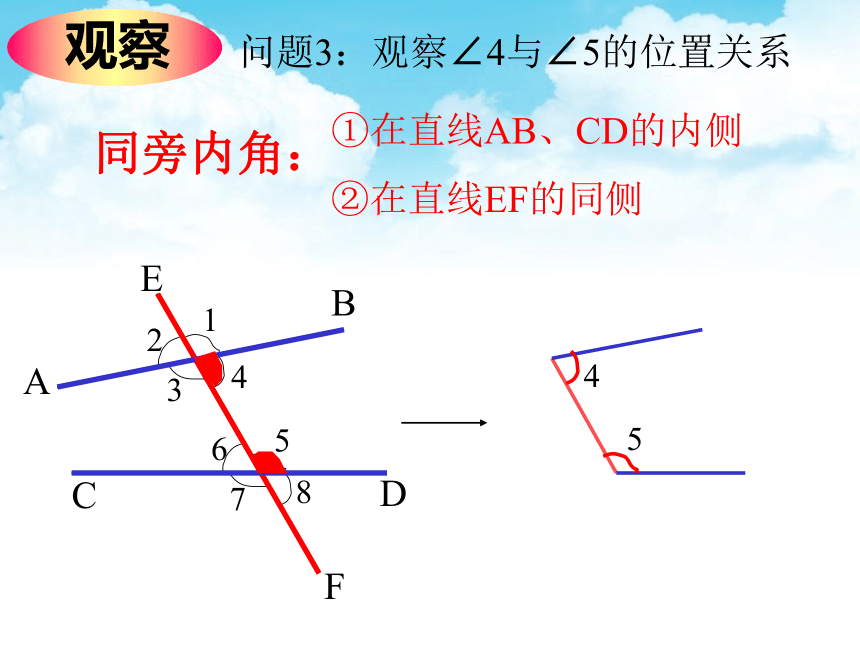
问题3:观察∠4与∠5的位置关系
①在直线AB、CD的内侧
②在直线EF的同侧
4
5
同旁内角:
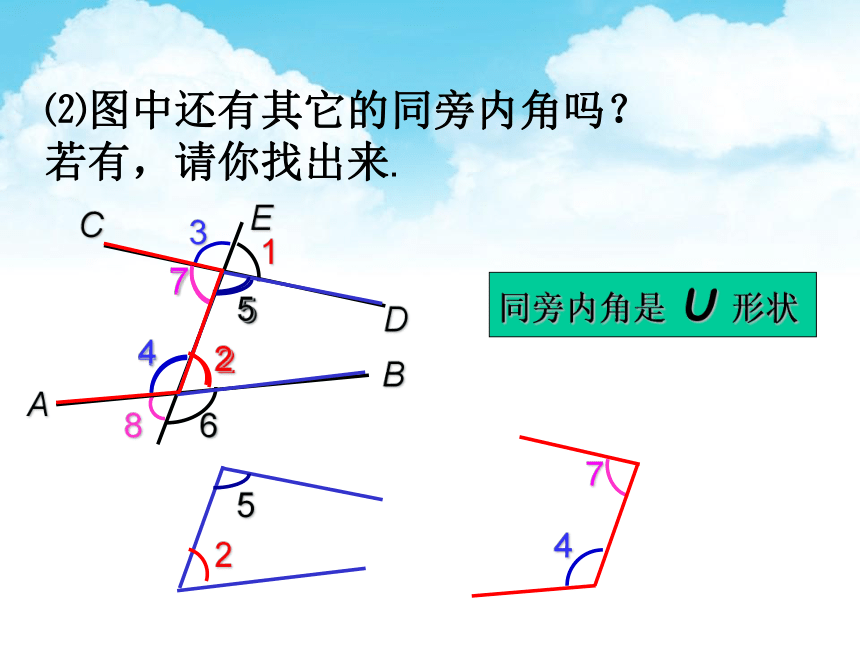
⑵图中还有其它的同旁内角吗?若有,请你找出来.
1
3
7
5
2
4
8
6
D
C
A
B
E
同旁内角是 U 形状
5
2
7
4
7
4
5
2
形如字母“U”
在截线同侧
夹在两条被截线之间
同旁内角
形如字母“Z”
(或反置)
在截线两侧(交错)
夹在两条被截线之间
内错角
形如字母“F”
(或倒置)
在截线同侧
在被截线同一方
同位角
图形结构特征
位 置 特 征
角的名称
活动三 基础小测
1.识别哪些角是同位角、内错角、 同旁内角。
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
2、下列各图中 与 哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
3、如图,(1) 和 是直线_____与直线____被直线______所截形成的__________。
(2) 和 是直线_____与直线____被直线______所截形成的_________。
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
1
4
A
B
C
D
2
3
A
B
D
C
(1)
(2)
例1. 如图,直线DE截直线AB,AC,构成8个角。 指出
所有的同位角、 内错角和同旁内角。
被截线
同位角
内错角
同旁内角
∠2和∠5
∠1和∠8
∠3和∠6
∠4和∠7
∠4和∠5
∠1和∠6
∠1和∠5
∠4和∠6
截线
活动四 强化 练习
例2
如图:直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和 ∠3,
∠1和 ∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
能力挑战: 看图填空
(1)若ED,BF被AB所截, 则∠1与_____是同位角。
∠2
能力挑战: 看图填空
(2)若ED,BC被AF所截, 则∠3与_____是内错角。
∠4
能力挑战: 看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
能力挑战: 看图填空
(4)∠2与∠4是_____和_____被 BC所截构成的______角。
AB
AF
同位
1
2
E
D
A
C
B
能力挑战 找出图中与∠1构成同旁内角的角
1
2
E
D
A
C
B
图中与∠1是同旁内角的角:
1
E
D
A
C
B
1
A
C
B
1
2
A
C
B
图中∠2的同旁内角的角:
1
2
E
D
A
C
B
1
2
A
C
B
2
A
C
B
2
E
D
A
C
B
小 结
1、这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
2、同位角、内错角、同旁内角的特点:
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
被截直线的同一方向
被截直线之间
被截直线之间
截线的同旁
截线的两旁
截线的同旁
作业:完成学案上的达标检查
数学 人教版 七年级下册
活动一:学案问题交流:
1.平面上两条直线有哪两种位置关系
(平行和相交)
1
2
3
4
5
6
7
8
2.两条直线相交有几个角
(4个)
3.两条直线与第三条直线相交呢?
(8个)
4.你能找出这8个角的关系吗?
∠1与∠3,∠2与∠4,
∠5与∠7,∠6与∠8
分别是对顶角。
5.这些角还有其它的关系吗
A
C
B
D
E
F
一、如图:1、怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
2、在两个交点处形成几个角?这些角有哪些与我们学过的有关?
7
1
2
3
4
5
6
8
观察
截线
被截直线
活 动 二 探究
观察
F
问题:1、观察∠1与∠5的位置关系
①在直线EF的同侧
②在直线AB、CD的同方向
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
同位角:
2.图中还有其它的同位角吗?若有,请你找出来.
F
1
2
3
4
5
6
7
8
D
C
A
B
E
①
5
1
②
6
2
③
3
7
同位角是 F 形状
8
4
④
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
问题:2、观察∠3与∠5的位置关系
①在直线AB、CD的内侧
②在直线EF的两侧
3
5
内错角:
⑵图中还有其它的内错角吗?若有,请你找出来.
1
3
7
5
2
4
8
6
D
C
A
B
E
7
2
5
4
7
2
5
4
内错角是 Z 形状
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
问题3:观察∠4与∠5的位置关系
①在直线AB、CD的内侧
②在直线EF的同侧
4
5
同旁内角:
⑵图中还有其它的同旁内角吗?若有,请你找出来.
1
3
7
5
2
4
8
6
D
C
A
B
E
同旁内角是 U 形状
5
2
7
4
7
4
5
2
形如字母“U”
在截线同侧
夹在两条被截线之间
同旁内角
形如字母“Z”
(或反置)
在截线两侧(交错)
夹在两条被截线之间
内错角
形如字母“F”
(或倒置)
在截线同侧
在被截线同一方
同位角
图形结构特征
位 置 特 征
角的名称
活动三 基础小测
1.识别哪些角是同位角、内错角、 同旁内角。
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
2、下列各图中 与 哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
3、如图,(1) 和 是直线_____与直线____被直线______所截形成的__________。
(2) 和 是直线_____与直线____被直线______所截形成的_________。
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
1
4
A
B
C
D
2
3
A
B
D
C
(1)
(2)
例1. 如图,直线DE截直线AB,AC,构成8个角。 指出
所有的同位角、 内错角和同旁内角。
被截线
同位角
内错角
同旁内角
∠2和∠5
∠1和∠8
∠3和∠6
∠4和∠7
∠4和∠5
∠1和∠6
∠1和∠5
∠4和∠6
截线
活动四 强化 练习
例2
如图:直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和 ∠3,
∠1和 ∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
能力挑战: 看图填空
(1)若ED,BF被AB所截, 则∠1与_____是同位角。
∠2
能力挑战: 看图填空
(2)若ED,BC被AF所截, 则∠3与_____是内错角。
∠4
能力挑战: 看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
能力挑战: 看图填空
(4)∠2与∠4是_____和_____被 BC所截构成的______角。
AB
AF
同位
1
2
E
D
A
C
B
能力挑战 找出图中与∠1构成同旁内角的角
1
2
E
D
A
C
B
图中与∠1是同旁内角的角:
1
E
D
A
C
B
1
A
C
B
1
2
A
C
B
图中∠2的同旁内角的角:
1
2
E
D
A
C
B
1
2
A
C
B
2
A
C
B
2
E
D
A
C
B
小 结
1、这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
2、同位角、内错角、同旁内角的特点:
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
被截直线的同一方向
被截直线之间
被截直线之间
截线的同旁
截线的两旁
截线的同旁
作业:完成学案上的达标检查
