人教版七年级下册5.3.2 命题定理证明 课件 (公开课)(共16张PPT)
文档属性
| 名称 | 人教版七年级下册5.3.2 命题定理证明 课件 (公开课)(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 13:03:46 | ||
图片预览






文档简介
(共16张PPT)
5.3.2 命题、定理、证明(2)
【第2课时】
歌德是18世纪德国的一位著名文艺大师,一天,他与一位批评家“狭路相逢”,这位文艺批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,边走边大声说道:“我从来不给傻子让路!”面对如此尴尬的局面,歌德笑容可掬,谦恭的闪在一旁,有礼貌地回答道:“呵呵,我可恰恰相反!”结果故作聪明的批评家,反倒自讨没趣,为什么呢?你知道其中的数学道理吗?这涉及到我们今天要学习的内容中的一个概念.
创设情境,引出新课
判断下列语句是不是命题?
(1)两点之间,线段最短;( )
(2)请画出两条互相平行的直线;( )
(3)如果两个角的和是90 ,那么这两个互余.( )
(4)两直线平行,同位角相等( )
(5)同位角相等,两直线平行。( )
(6)兔子是四只脚( )
√
√
回忆巩固
√
√
√
×
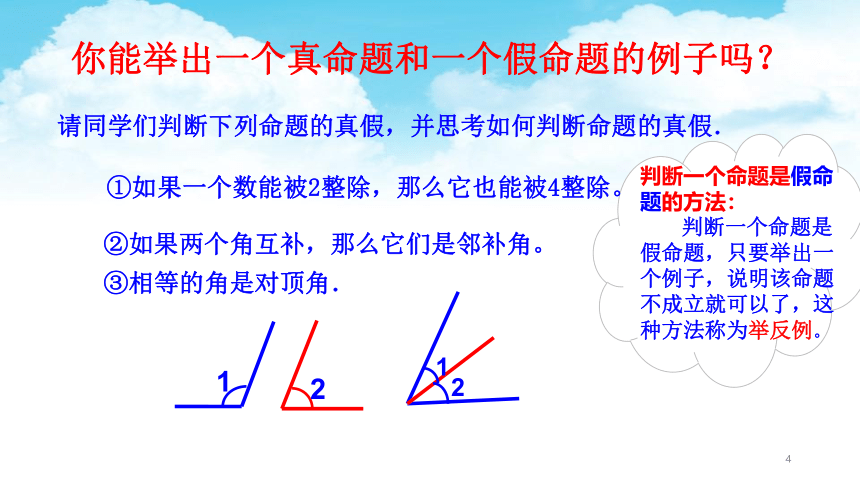
②如果两个角互补,那么它们是邻补角。①如果一个数能被2整除,那么它也能被4整除。请同学们判断下列命题的真假,并思考如何判断命题的真假.③相等的角是对顶角.1212你能举出一个真命题和一个假命题的例子吗?判断一个命题是假命题的方法:判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
回忆巩固
平行线的性质
性质1:两直线平行线,同位角相等
性质2:两直线平行线,内错角相等
性质3:两直线平行线,同旁内角互补
平行线的判定
判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角互补,两直线平行。
1、数学中有些命题的正确性是人们在长期实践中总结出来的基本事实,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理。
2、有些命题的正确性需要经过推理证实,这样得到的真命题叫做定理。
定理可以进一步作为判断其他命题真假的依据,
公理和定理都可作为判断其他命题真假的依据。
一个命题的正确性需要经过推理,才能作出判断,这个推理过程就叫做证明。
命题1: 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
(1)命题1是真命题还是假命题?
(2)你能将命题1所叙述的内容
用图形语言来表达吗?
(3)这个命题的题设和结论分别是什么呢?
引例:
命题1 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
题设:在同一平面内,一条直线垂直于两条平行线中的一条;
结论:这条直线也垂直于两条平行线中的另一条.
(4)你能结合图形用几何语言表述命题的题设和结论吗?
命题1 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
已知:b∥c, a⊥b .
求证:a⊥c.
(5)请同学们思考如何利用已经学过的定义定理
来证明这个结论呢?
已知:b∥c,a⊥b .
求证:a⊥c.
证明:∵ a⊥b(已知),
又∵ b∥c(已知),
∴∠1=∠2(两直线平行,同位角相等).
∴∠2=∠1=90 (等量代换).
∴∠1=90 (垂直的定义).
∴ a⊥c(垂直的定义).
1.如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
证明: ∵由AC∥DE (已知)
∴ ∠ACD= ∠2 (两直线平行,
内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD(等量代换)
∴AB ∥ CD(内错角相等,两直线平行)
A
D
B
E
1
2
C
三、练习巩固
2.已知:如图1,∠1=∠2,∠3=∠4,求证:EG//FH.
1、公理:人们长期以来在实践中总结出来的,并作为判断其他
命题真假的根据的命题,叫做公理。
2、定理:经过推理论证为正确的命题叫定理。也可作为继续推
理的依据。
3、判断一个命题是真命题,可以从公理或定理出发,用逻辑推理
的方法证明(公理和定理都是真命题);
判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
课堂小节
课堂小节
1.如何判断一个命题的真假?
2.谈谈你对证明的理解。
判断一个命题真假的方法:
利用已有的知识,通过观察、验证、推理、举反例等方法。
判断一个命题是假命题的方法:
判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
证明中的每一步推理都要有根据,不能“想当然”。这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理
再 见
作业布置:P22 练习1
习题3
5.3.2 命题、定理、证明(2)
【第2课时】
歌德是18世纪德国的一位著名文艺大师,一天,他与一位批评家“狭路相逢”,这位文艺批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,边走边大声说道:“我从来不给傻子让路!”面对如此尴尬的局面,歌德笑容可掬,谦恭的闪在一旁,有礼貌地回答道:“呵呵,我可恰恰相反!”结果故作聪明的批评家,反倒自讨没趣,为什么呢?你知道其中的数学道理吗?这涉及到我们今天要学习的内容中的一个概念.
创设情境,引出新课
判断下列语句是不是命题?
(1)两点之间,线段最短;( )
(2)请画出两条互相平行的直线;( )
(3)如果两个角的和是90 ,那么这两个互余.( )
(4)两直线平行,同位角相等( )
(5)同位角相等,两直线平行。( )
(6)兔子是四只脚( )
√
√
回忆巩固
√
√
√
×
②如果两个角互补,那么它们是邻补角。①如果一个数能被2整除,那么它也能被4整除。请同学们判断下列命题的真假,并思考如何判断命题的真假.③相等的角是对顶角.1212你能举出一个真命题和一个假命题的例子吗?判断一个命题是假命题的方法:判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
回忆巩固
平行线的性质
性质1:两直线平行线,同位角相等
性质2:两直线平行线,内错角相等
性质3:两直线平行线,同旁内角互补
平行线的判定
判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角互补,两直线平行。
1、数学中有些命题的正确性是人们在长期实践中总结出来的基本事实,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理。
2、有些命题的正确性需要经过推理证实,这样得到的真命题叫做定理。
定理可以进一步作为判断其他命题真假的依据,
公理和定理都可作为判断其他命题真假的依据。
一个命题的正确性需要经过推理,才能作出判断,这个推理过程就叫做证明。
命题1: 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
(1)命题1是真命题还是假命题?
(2)你能将命题1所叙述的内容
用图形语言来表达吗?
(3)这个命题的题设和结论分别是什么呢?
引例:
命题1 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
题设:在同一平面内,一条直线垂直于两条平行线中的一条;
结论:这条直线也垂直于两条平行线中的另一条.
(4)你能结合图形用几何语言表述命题的题设和结论吗?
命题1 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
已知:b∥c, a⊥b .
求证:a⊥c.
(5)请同学们思考如何利用已经学过的定义定理
来证明这个结论呢?
已知:b∥c,a⊥b .
求证:a⊥c.
证明:∵ a⊥b(已知),
又∵ b∥c(已知),
∴∠1=∠2(两直线平行,同位角相等).
∴∠2=∠1=90 (等量代换).
∴∠1=90 (垂直的定义).
∴ a⊥c(垂直的定义).
1.如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
证明: ∵由AC∥DE (已知)
∴ ∠ACD= ∠2 (两直线平行,
内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD(等量代换)
∴AB ∥ CD(内错角相等,两直线平行)
A
D
B
E
1
2
C
三、练习巩固
2.已知:如图1,∠1=∠2,∠3=∠4,求证:EG//FH.
1、公理:人们长期以来在实践中总结出来的,并作为判断其他
命题真假的根据的命题,叫做公理。
2、定理:经过推理论证为正确的命题叫定理。也可作为继续推
理的依据。
3、判断一个命题是真命题,可以从公理或定理出发,用逻辑推理
的方法证明(公理和定理都是真命题);
判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
课堂小节
课堂小节
1.如何判断一个命题的真假?
2.谈谈你对证明的理解。
判断一个命题真假的方法:
利用已有的知识,通过观察、验证、推理、举反例等方法。
判断一个命题是假命题的方法:
判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
证明中的每一步推理都要有根据,不能“想当然”。这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理
再 见
作业布置:P22 练习1
习题3
