2022-2023学年人教版八年级数学下册19.2.3一次函数与方程、不等式第一课时 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册19.2.3一次函数与方程、不等式第一课时 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 54.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 14:34:04 | ||
图片预览




文档简介
(共22张PPT)
一次函数与方程、不等式
——第一课时
授课人 xxx
复习引入
x
2x
2x+1
2x+1=0
2x+1>0
y=2x+1
那你会不会画出y=2x+1的图象呢?
探究新知——一次函数与一元一次方程
计算下面3个方程的解:
(1)2x+1=0 (2) 2x+1=3 (3)2x+1=-1
一元一次方程 解
2x+1=0 x=-
2x+1=3 x=1
2x+1=-1 x=-1
探究新知——一次函数与一元一次方程
思考
观察下面3个方程:
(1)2x+1=0 (2)2x+1=3 (3)2x+1=-1
你能否从函数的角度对解这3个方程进行解释吗?
有什么共同点和不同点?
共同点:
不同点:
等号左边都是2x+1
等号右边分别是0,3,-1
探究新知——一次函数与一元一次方程
你能否从函数的角度对解这3个方程进行解释吗?
(1)2x+1=0 (2) 2x+1=3 (3)2x+1=-1
想一想
y=2x+1
能否找到一个函数可以将这3个方程联系起来
探究新知——一次函数与一元一次方程
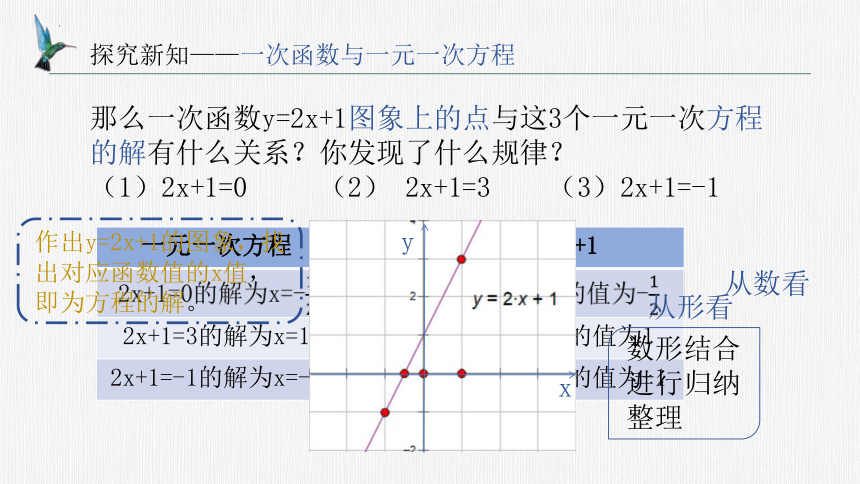
那么一次函数y=2x+1图象上的点与这3个一元一次方程的解有什么关系?你发现了什么规律?
(1)2x+1=0 (2) 2x+1=3 (3)2x+1=-1
一元一次方程 一次函数y=2x+1
2x+1=0的解为x=- 当y=0时,自变量x的值为-
2x+1=3的解为x=1 当y=3时,自变量x的值为1
2x+1=-1的解为x=-1 当y=-1时,自变量x的值为-1
从数看
x
y
从形看
作出y=2x+1的图象,找出对应函数值的x值,即为方程的解。
数形结合进行归纳整理
探究新知——一次函数与一元一次方程
2 x+1=0
2 x+1=3
2 x+1=-1
方程的角度
函数的角度
y=2x+1
0=2x+1
3=2x+1
-1=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=2x+1
解一元一次方程
一次函数y取某个值的时候求x
归纳
探究新知——一次函数与一元一次方程
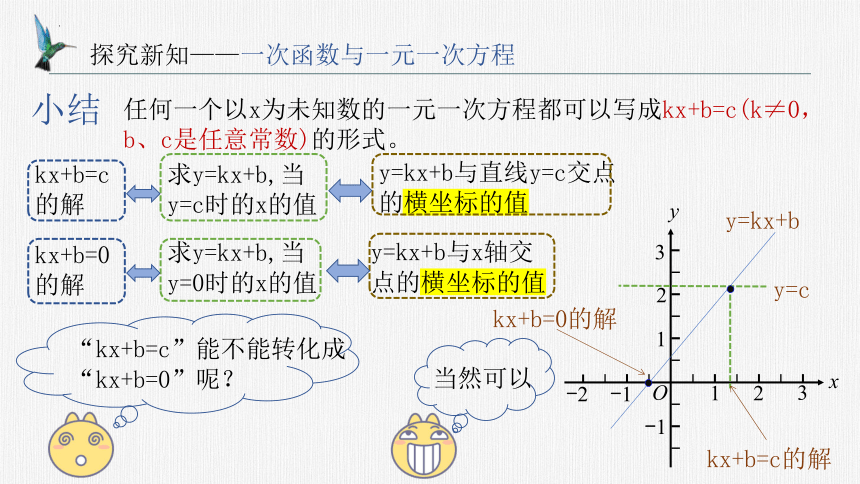
任何一个以x为未知数的一元一次方程都可以写成kx+b=c(k≠0,b、c是任意常数)的形式。
小结
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=kx+b
kx+b=0的解
y=kx+b与直线y=c交点的横坐标的值
kx+b=c的解
y=c
kx+b=0
的解
求y=kx+b,当y=c时的x的值
y=kx+b与x轴交点的横坐标的值
kx+b=c
的解
求y=kx+b,当y=0时的x的值
“kx+b=c”能不能转化成“kx+b=0”呢?
当然可以
探究新知——一次函数与一元一次方程
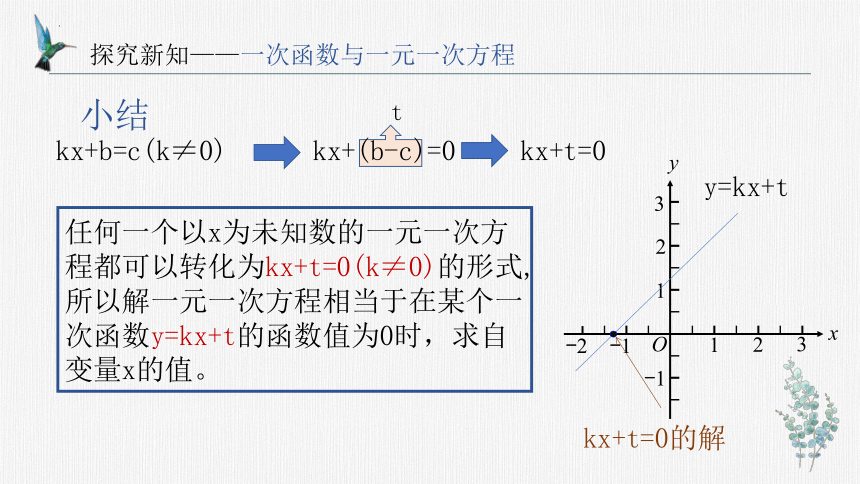
小结
kx+b=c(k≠0)
3
2
1
2
1
-2
O
x
y
-1
-1
3
kx+(b-c)=0
任何一个以x为未知数的一元一次方程都可以转化为kx+t=0(k≠0)的形式,
所以解一元一次方程相当于在某个一次函数y=kx+t的函数值为0时,求自变量x的值。
y=kx+t
kx+t=0的解
kx+t=0
t
例题讲解
例1、一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
3
2
1
2
1
-2
O
x
y
-1
-1
3
A.x=2 B.y=2 C.x=-1 D.y=-1
y=0
x=
探究新知——一次函数与一元一次不等式
思考
观察下面3个不等式:
(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
有什么共同点和不同点?
相同点:
不同点:
不等号左边都是3x+2
不等号及不等号右边不一样
你又如何从函数的角度对解这3个不等式进行解释呢?
想一想:类比一次函数和一元一次方程的关系,你能从函数角度对不等式进行解释吗?
探究新知——一次函数与一元一次不等式
思考
观察下面3个不等式:
(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
有什么共同点和不同点?
相同点:
不同点:
不等号左边都是3x+2
不等号及不等号右边不一样
你又如何从函数的角度对解这3个不等式进行解释呢?
想一想:类比一次函数和一元一次方程的关系,你能从函数角度对不等式进行解释吗?
探究新知——一次函数与一元一次不等式
你又如何从函数的角度对解这3个不等式进行解释呢?
(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
从“数”看 从“形”看
一元一次不等式 一次函数
3x+2>2的解为: 当 时,自变量x的取值范围为
3x+2<0的解为: 当 时,自变量x的取值范围为
3x+2<-1的解为: 当 时,自变量x的取值范围为
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=3x+2
x>0
x<-1
y>2
x<-1
x>0
y<0
y<-1
x<-
x<-
探究新知——一次函数与一元一次不等式
归纳小结
任何一个以x为未知数的一元一次不等式都可以写成kx+b>c或kx+b3
2
1
2
1
-2
O
x
y
-1
-1
3
直线y=kx+b在直线y=c下方的部分对应的x的取值范围
kx+b>c的解集
直线y=kx+b在直线y=c上方的部分对应的x的取值范围
kx+b当y>c时,求相应的自变量x的取值范围
当yy=kx+b
y=c
kx+b>c的解集
kx+b探究新知——一次函数与一元一次不等式
归纳小结
kx+b>c或kx+b3
2
1
2
1
-2
O
x
y
-1
-1
3
kx+t>0或kx+t<0(k≠0)
任何一个以x为未知数的一元一次不等式都可以变形为kx+t>0或kx+t<0(k≠0)的形式。
所以解一元一次不等式相当于在某个一次函数y=kx+t的函数值大于0或小于0时,求自变量x的取值范围.
求直线y=kx+t位于x轴上方(或下方)的部分所对应的x的取值范围。
y=kx+t
kx+t<0的解集
kx+t>0的解集
口诀:找界点,看上下,答左右。
例题讲解
例2、如图,已知直线y=ax+b,回答下列问题:
(1)方程ax+b=0的解为
(2)方程ax+b=-1的解为
(3)当x 时,y=0
(4)当x 时,y<0
(5)当x 时,y>0
(6)不等式ax+b≥-1的解集是
3
2
1
2
1
-2
O
x
y
-1
-1
3
>2
<2
x=2
=2
x=0
x≥0
y=-1
口诀:找界点,看上下,答左右。
y
随堂练习
1、如图,一次函数y=kx+b的图象经过点(0,3),(3,-1),则关于x的不等式kx+b+1<0的解集为
3
2
1
2
1
-2
O
x
y
-1
-1
3
x>3
kx+b<-1
y=-1
随堂练习
2、已知不等式ax+b<0的解x>-2是,下列有可能是函数y=ax+b的图象的是
3
2
1
2
1
-2
O
x
y
-1
3
3
2
1
2
1
-2
O
x
y
-1
3
3
2
1
2
1
-2
O
x
y
-1
3
3
2
1
2
1
-2
O
x
y
-1
3
A
B
C
D
C
随堂练习
3、在如图所示的平面直角坐标系中画出函数y=x-2的图象,并利用图象解决下列问题:
(1)求方程-x-2=0的解;
(2)求不等式-x-2<0的解集;
(3)若-4≤y≤2,求x的取值范围.
解:(1)x=-3
(2)x>-3
(3)-6≤x≤3
课堂小结
1、方程与函数之间互相联系,从函数的角度可以把它们统一起来
2、解一元一次方程kx+t=0(k≠0)相当于在某个一次函数y=kx+t的函数值为0时,求自变量x的值。即直线y=kx+t与x轴的交点坐标。
3、解一元一次不等式kx+t>0或kx+t<0(k≠0)相当于在某个一次函数y=kx+t的函数值大于0或小于0时,求自变量x的取值范围.求直线y=kx+t位于x轴上方(或下方)的部分所对应的x的取值范围。
4、口诀:找界点,看上下,答左右。
你学会了吗?
思考
2x-y=-1是一次函数还是二元一次方程?
1、完成课本P99
第10题
第13题
2、预习
课 后 作 业
感谢观看
一次函数与方程、不等式
——第一课时
授课人 xxx
复习引入
x
2x
2x+1
2x+1=0
2x+1>0
y=2x+1
那你会不会画出y=2x+1的图象呢?
探究新知——一次函数与一元一次方程
计算下面3个方程的解:
(1)2x+1=0 (2) 2x+1=3 (3)2x+1=-1
一元一次方程 解
2x+1=0 x=-
2x+1=3 x=1
2x+1=-1 x=-1
探究新知——一次函数与一元一次方程
思考
观察下面3个方程:
(1)2x+1=0 (2)2x+1=3 (3)2x+1=-1
你能否从函数的角度对解这3个方程进行解释吗?
有什么共同点和不同点?
共同点:
不同点:
等号左边都是2x+1
等号右边分别是0,3,-1
探究新知——一次函数与一元一次方程
你能否从函数的角度对解这3个方程进行解释吗?
(1)2x+1=0 (2) 2x+1=3 (3)2x+1=-1
想一想
y=2x+1
能否找到一个函数可以将这3个方程联系起来
探究新知——一次函数与一元一次方程
那么一次函数y=2x+1图象上的点与这3个一元一次方程的解有什么关系?你发现了什么规律?
(1)2x+1=0 (2) 2x+1=3 (3)2x+1=-1
一元一次方程 一次函数y=2x+1
2x+1=0的解为x=- 当y=0时,自变量x的值为-
2x+1=3的解为x=1 当y=3时,自变量x的值为1
2x+1=-1的解为x=-1 当y=-1时,自变量x的值为-1
从数看
x
y
从形看
作出y=2x+1的图象,找出对应函数值的x值,即为方程的解。
数形结合进行归纳整理
探究新知——一次函数与一元一次方程
2 x+1=0
2 x+1=3
2 x+1=-1
方程的角度
函数的角度
y=2x+1
0=2x+1
3=2x+1
-1=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=2x+1
解一元一次方程
一次函数y取某个值的时候求x
归纳
探究新知——一次函数与一元一次方程
任何一个以x为未知数的一元一次方程都可以写成kx+b=c(k≠0,b、c是任意常数)的形式。
小结
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=kx+b
kx+b=0的解
y=kx+b与直线y=c交点的横坐标的值
kx+b=c的解
y=c
kx+b=0
的解
求y=kx+b,当y=c时的x的值
y=kx+b与x轴交点的横坐标的值
kx+b=c
的解
求y=kx+b,当y=0时的x的值
“kx+b=c”能不能转化成“kx+b=0”呢?
当然可以
探究新知——一次函数与一元一次方程
小结
kx+b=c(k≠0)
3
2
1
2
1
-2
O
x
y
-1
-1
3
kx+(b-c)=0
任何一个以x为未知数的一元一次方程都可以转化为kx+t=0(k≠0)的形式,
所以解一元一次方程相当于在某个一次函数y=kx+t的函数值为0时,求自变量x的值。
y=kx+t
kx+t=0的解
kx+t=0
t
例题讲解
例1、一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
3
2
1
2
1
-2
O
x
y
-1
-1
3
A.x=2 B.y=2 C.x=-1 D.y=-1
y=0
x=
探究新知——一次函数与一元一次不等式
思考
观察下面3个不等式:
(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
有什么共同点和不同点?
相同点:
不同点:
不等号左边都是3x+2
不等号及不等号右边不一样
你又如何从函数的角度对解这3个不等式进行解释呢?
想一想:类比一次函数和一元一次方程的关系,你能从函数角度对不等式进行解释吗?
探究新知——一次函数与一元一次不等式
思考
观察下面3个不等式:
(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
有什么共同点和不同点?
相同点:
不同点:
不等号左边都是3x+2
不等号及不等号右边不一样
你又如何从函数的角度对解这3个不等式进行解释呢?
想一想:类比一次函数和一元一次方程的关系,你能从函数角度对不等式进行解释吗?
探究新知——一次函数与一元一次不等式
你又如何从函数的角度对解这3个不等式进行解释呢?
(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
从“数”看 从“形”看
一元一次不等式 一次函数
3x+2>2的解为: 当 时,自变量x的取值范围为
3x+2<0的解为: 当 时,自变量x的取值范围为
3x+2<-1的解为: 当 时,自变量x的取值范围为
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=3x+2
x>0
x<-1
y>2
x<-1
x>0
y<0
y<-1
x<-
x<-
探究新知——一次函数与一元一次不等式
归纳小结
任何一个以x为未知数的一元一次不等式都可以写成kx+b>c或kx+b
2
1
2
1
-2
O
x
y
-1
-1
3
直线y=kx+b在直线y=c下方的部分对应的x的取值范围
kx+b>c的解集
直线y=kx+b在直线y=c上方的部分对应的x的取值范围
kx+b
当y
y=c
kx+b>c的解集
kx+b
归纳小结
kx+b>c或kx+b
2
1
2
1
-2
O
x
y
-1
-1
3
kx+t>0或kx+t<0(k≠0)
任何一个以x为未知数的一元一次不等式都可以变形为kx+t>0或kx+t<0(k≠0)的形式。
所以解一元一次不等式相当于在某个一次函数y=kx+t的函数值大于0或小于0时,求自变量x的取值范围.
求直线y=kx+t位于x轴上方(或下方)的部分所对应的x的取值范围。
y=kx+t
kx+t<0的解集
kx+t>0的解集
口诀:找界点,看上下,答左右。
例题讲解
例2、如图,已知直线y=ax+b,回答下列问题:
(1)方程ax+b=0的解为
(2)方程ax+b=-1的解为
(3)当x 时,y=0
(4)当x 时,y<0
(5)当x 时,y>0
(6)不等式ax+b≥-1的解集是
3
2
1
2
1
-2
O
x
y
-1
-1
3
>2
<2
x=2
=2
x=0
x≥0
y=-1
口诀:找界点,看上下,答左右。
y
随堂练习
1、如图,一次函数y=kx+b的图象经过点(0,3),(3,-1),则关于x的不等式kx+b+1<0的解集为
3
2
1
2
1
-2
O
x
y
-1
-1
3
x>3
kx+b<-1
y=-1
随堂练习
2、已知不等式ax+b<0的解x>-2是,下列有可能是函数y=ax+b的图象的是
3
2
1
2
1
-2
O
x
y
-1
3
3
2
1
2
1
-2
O
x
y
-1
3
3
2
1
2
1
-2
O
x
y
-1
3
3
2
1
2
1
-2
O
x
y
-1
3
A
B
C
D
C
随堂练习
3、在如图所示的平面直角坐标系中画出函数y=x-2的图象,并利用图象解决下列问题:
(1)求方程-x-2=0的解;
(2)求不等式-x-2<0的解集;
(3)若-4≤y≤2,求x的取值范围.
解:(1)x=-3
(2)x>-3
(3)-6≤x≤3
课堂小结
1、方程与函数之间互相联系,从函数的角度可以把它们统一起来
2、解一元一次方程kx+t=0(k≠0)相当于在某个一次函数y=kx+t的函数值为0时,求自变量x的值。即直线y=kx+t与x轴的交点坐标。
3、解一元一次不等式kx+t>0或kx+t<0(k≠0)相当于在某个一次函数y=kx+t的函数值大于0或小于0时,求自变量x的取值范围.求直线y=kx+t位于x轴上方(或下方)的部分所对应的x的取值范围。
4、口诀:找界点,看上下,答左右。
你学会了吗?
思考
2x-y=-1是一次函数还是二元一次方程?
1、完成课本P99
第10题
第13题
2、预习
课 后 作 业
感谢观看
