9.1.1 不等式及其解集 课件(共26张PPT)
文档属性
| 名称 | 9.1.1 不等式及其解集 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-26 00:45:27 | ||
图片预览







文档简介
(共26张PPT)
第九章 不等式与不等式组
9.1 不等式
9.1.1 不等式及其解集
学习目标
1.理解不等式、不等式的解、不等式的解集的概念.
2.能在数轴上表示不等式的解集.
3.能根据不等关系列简单的不等式.
重点:不等式的概念,不等式的解、解集的概念,在数轴上表示不等式的解集.
难点:不等式的解集的概念.
课前预习
阅读课本第P114-115页内容,学习本节主要内容.
未知数的值
所有
>
的解
≠
<
解
集
许多人在童年时期,都玩过坐跷跷板的游戏,当一个成年人和一个儿童同时坐上等臂长的跷跷板的两边时会发生什么现象呢?
新课导入
思考
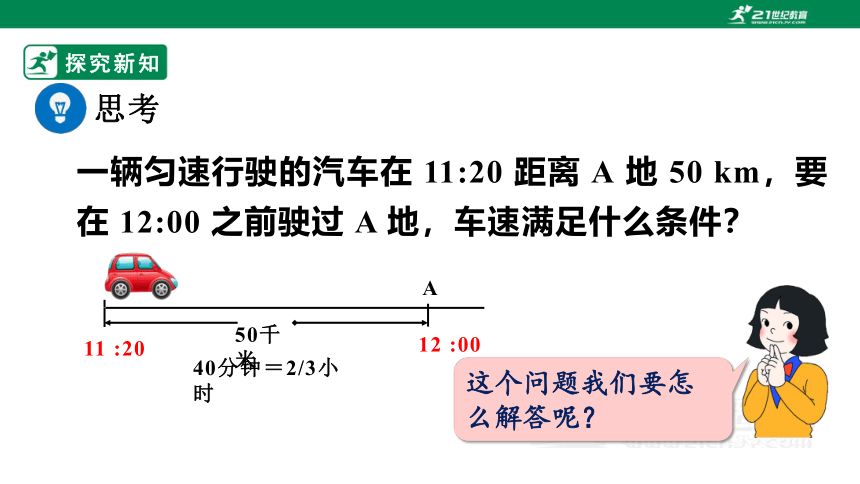
一辆匀速行驶的汽车在 11:20 距离 A 地 50 km,要在 12:00 之前驶过 A 地,车速满足什么条件?
这个问题我们要怎么解答呢?
A
50千米
11 :20
12 :00
40分钟=2/3小时
探究新知
分析:
设车速是 x 千米/时.
从时间上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 50 km 所用的时间不到 h,即:
……①
从路程上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即:
……②
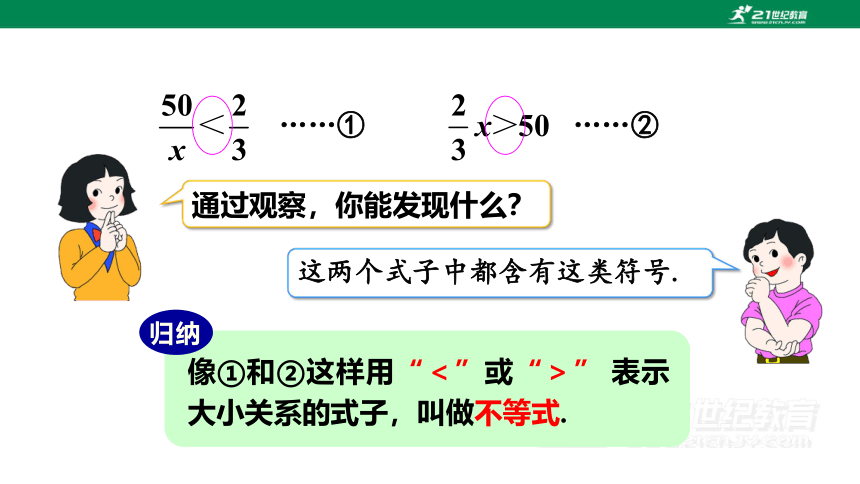
……①
……②
通过观察,你能发现什么?
这两个式子中都含有这类符号.
像①和②这样用“<”或“>” 表示大小关系的式子,叫做不等式.
归纳
像a+2≠a – 2这样的式子是不等式吗?
像a+2≠a – 2这样用符号 “≠”表示不等关系的式子也是不等式.
像3<4,– 1 > – 2这样不含未知数的式子是不等式吗?
它们也是不等式.
思考
不等式的定义
用“<”或“>”或“≠”表示大小关系的式子,叫做不等式.
注意:不等式中不一定要含有未知数.
知识归纳
①a是正数; ②a是负数;
③a与5的和小于7; ④a与2的差大于-1;
⑤a的4倍大于8; ⑥a的一半小于3.
①a>0; ②a<0; ③a+5<7;
④a – 2>– 1 ; ⑤4a>8; ⑥ a<3.
解:
用不等式表示
随堂练习
……①
……②
你能以第②个式子为例,明确的得出 x 应取哪些值吗?
不等式的解与解集
1.当x=80时, ;
2.当x=78时, ;
3.当x=75时, ;
4.当x=72时, .
在式子②中:
探究新知
也就是说当x取某些值(如80,78)时不等式 成立,当x取某些值(如75,72)时,不等式 不成立.
我们把使不等式成立的未知数的值叫做不等式的解.
上述式子②的解你发现了什么?
当x>75时,不等式 总成立;而当x<75或x=75时,不等式 不成立.
任何一个大于75的数都是不等式 的解,任何一个小于或等于75的数都不是不等式 的解.因此x>75表示了能使不等式 成立的x的取值范围.
思考
除了80和78,不等式还有其他解吗?如果有,这些解应满足什么条件?
0
75
在数轴上表示如下图:
在表示75的点上画空心圆圈,表示不包含这一点.
由上图可知,在前面问题中,汽车要在12:00之前驶过A地,车速必须大于75km/h.
由不等式①能得出这个结果吗?
我们可以怎么表示不等式的解集呢?
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
>,<画空心圆.
知识归纳
不等式的解 不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
-4,-2.5,0,1,2.5,3,
3.2,4.8,8,12
1.下列数中哪些是不等式 x+3>6的解?哪些不是?
3.2,4.8,8,12是 x+3>6的解,
其余不是.
随堂练习
(a)解集为:x>3.
(a)x+3>6;(b)2x<8;(c)x-2>0.
2.直接说出下面不等式的解集,并用数轴把它们表示出来.
0
4
0
3
0
2
(c)解集为:x>2.
(b)解集为:x<4.
例1 下列式子中哪些是不等式?
(1)a+b=b+a;(2)-3>-5;(3)x≠1;
(4)x+3>6;(5)2m解:不等式有(2)(3)(4)(5).
例题分析
例2 根据下列数量关系,列出不等式:
(1)x与2的和是负数;
(2)m与1的相反数的和是非负数;
(3)a与-2的差不大于它的3倍;
(4)a,b两数的平方和不小于它们的积的两倍.
解:(1)x+2<0;
(2)m-1≥0;
(3)a+2≤3a;
(4)a2+b2≥2ab.
例3 直接写出下列不等式的解集,并在数轴上表示出来.
(1)x+2<1的解集是___________;
(2)4x>6的解集是________.
x<-1
x>
-1
0
1
-1
0
1
2
1.给出下面5个式子:①3>0;②4x+3y≠0;③x=3;④x-1;
⑤x+2<3,其中不等式有( )
A.2个 B.3个
C.4个 D.5个
B
随堂练习
2.下列数量关系用不等式表示错误的是( )
A.若a是负数,则a<0
B.若m的值小于1,则m<1
C.若x与-1的和大于0,则x-1>0
D.若a的 大于b,则 a≠b
D
3.恩格尔系数n是指家庭日常饮食占家庭总支出的比例,它反映了居民家庭的实际生活水平,各种类型家庭的n值如下表所示:
家庭类型 贫困 温饱 小康 发达国家 最富裕国家
n 75%以上 50%~75% 40%~49% 20%~39% 不到20%
如果用含n的不等式表示,那么贫困家庭为________,最富裕国家家庭为__________;当某一家庭n=0.6时,表明该家庭的实际生活水平是______.
n>75%
n<20%
温饱
不等式
实际问题中不等式的表示
概念
解、解集
课堂小结
1.教材P 119~120习题9.1第1,2题;
2.完成对应课时练习.
作业布置
第九章 不等式与不等式组
9.1 不等式
9.1.1 不等式及其解集
学习目标
1.理解不等式、不等式的解、不等式的解集的概念.
2.能在数轴上表示不等式的解集.
3.能根据不等关系列简单的不等式.
重点:不等式的概念,不等式的解、解集的概念,在数轴上表示不等式的解集.
难点:不等式的解集的概念.
课前预习
阅读课本第P114-115页内容,学习本节主要内容.
未知数的值
所有
>
的解
≠
<
解
集
许多人在童年时期,都玩过坐跷跷板的游戏,当一个成年人和一个儿童同时坐上等臂长的跷跷板的两边时会发生什么现象呢?
新课导入
思考
一辆匀速行驶的汽车在 11:20 距离 A 地 50 km,要在 12:00 之前驶过 A 地,车速满足什么条件?
这个问题我们要怎么解答呢?
A
50千米
11 :20
12 :00
40分钟=2/3小时
探究新知
分析:
设车速是 x 千米/时.
从时间上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 50 km 所用的时间不到 h,即:
……①
从路程上看
汽车要在 12:00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即:
……②
……①
……②
通过观察,你能发现什么?
这两个式子中都含有这类符号.
像①和②这样用“<”或“>” 表示大小关系的式子,叫做不等式.
归纳
像a+2≠a – 2这样的式子是不等式吗?
像a+2≠a – 2这样用符号 “≠”表示不等关系的式子也是不等式.
像3<4,– 1 > – 2这样不含未知数的式子是不等式吗?
它们也是不等式.
思考
不等式的定义
用“<”或“>”或“≠”表示大小关系的式子,叫做不等式.
注意:不等式中不一定要含有未知数.
知识归纳
①a是正数; ②a是负数;
③a与5的和小于7; ④a与2的差大于-1;
⑤a的4倍大于8; ⑥a的一半小于3.
①a>0; ②a<0; ③a+5<7;
④a – 2>– 1 ; ⑤4a>8; ⑥ a<3.
解:
用不等式表示
随堂练习
……①
……②
你能以第②个式子为例,明确的得出 x 应取哪些值吗?
不等式的解与解集
1.当x=80时, ;
2.当x=78时, ;
3.当x=75时, ;
4.当x=72时, .
在式子②中:
探究新知
也就是说当x取某些值(如80,78)时不等式 成立,当x取某些值(如75,72)时,不等式 不成立.
我们把使不等式成立的未知数的值叫做不等式的解.
上述式子②的解你发现了什么?
当x>75时,不等式 总成立;而当x<75或x=75时,不等式 不成立.
任何一个大于75的数都是不等式 的解,任何一个小于或等于75的数都不是不等式 的解.因此x>75表示了能使不等式 成立的x的取值范围.
思考
除了80和78,不等式还有其他解吗?如果有,这些解应满足什么条件?
0
75
在数轴上表示如下图:
在表示75的点上画空心圆圈,表示不包含这一点.
由上图可知,在前面问题中,汽车要在12:00之前驶过A地,车速必须大于75km/h.
由不等式①能得出这个结果吗?
我们可以怎么表示不等式的解集呢?
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
>,<画空心圆.
知识归纳
不等式的解 不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
-4,-2.5,0,1,2.5,3,
3.2,4.8,8,12
1.下列数中哪些是不等式 x+3>6的解?哪些不是?
3.2,4.8,8,12是 x+3>6的解,
其余不是.
随堂练习
(a)解集为:x>3.
(a)x+3>6;(b)2x<8;(c)x-2>0.
2.直接说出下面不等式的解集,并用数轴把它们表示出来.
0
4
0
3
0
2
(c)解集为:x>2.
(b)解集为:x<4.
例1 下列式子中哪些是不等式?
(1)a+b=b+a;(2)-3>-5;(3)x≠1;
(4)x+3>6;(5)2m
例题分析
例2 根据下列数量关系,列出不等式:
(1)x与2的和是负数;
(2)m与1的相反数的和是非负数;
(3)a与-2的差不大于它的3倍;
(4)a,b两数的平方和不小于它们的积的两倍.
解:(1)x+2<0;
(2)m-1≥0;
(3)a+2≤3a;
(4)a2+b2≥2ab.
例3 直接写出下列不等式的解集,并在数轴上表示出来.
(1)x+2<1的解集是___________;
(2)4x>6的解集是________.
x<-1
x>
-1
0
1
-1
0
1
2
1.给出下面5个式子:①3>0;②4x+3y≠0;③x=3;④x-1;
⑤x+2<3,其中不等式有( )
A.2个 B.3个
C.4个 D.5个
B
随堂练习
2.下列数量关系用不等式表示错误的是( )
A.若a是负数,则a<0
B.若m的值小于1,则m<1
C.若x与-1的和大于0,则x-1>0
D.若a的 大于b,则 a≠b
D
3.恩格尔系数n是指家庭日常饮食占家庭总支出的比例,它反映了居民家庭的实际生活水平,各种类型家庭的n值如下表所示:
家庭类型 贫困 温饱 小康 发达国家 最富裕国家
n 75%以上 50%~75% 40%~49% 20%~39% 不到20%
如果用含n的不等式表示,那么贫困家庭为________,最富裕国家家庭为__________;当某一家庭n=0.6时,表明该家庭的实际生活水平是______.
n>75%
n<20%
温饱
不等式
实际问题中不等式的表示
概念
解、解集
课堂小结
1.教材P 119~120习题9.1第1,2题;
2.完成对应课时练习.
作业布置
