6.3.1平面向量基本定理 课件(共22张PPT)
文档属性
| 名称 | 6.3.1平面向量基本定理 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-25 21:39:28 | ||
图片预览




文档简介
第1课时
【第六章 平面向量及其应用】
6.3.1平面向量基本定理
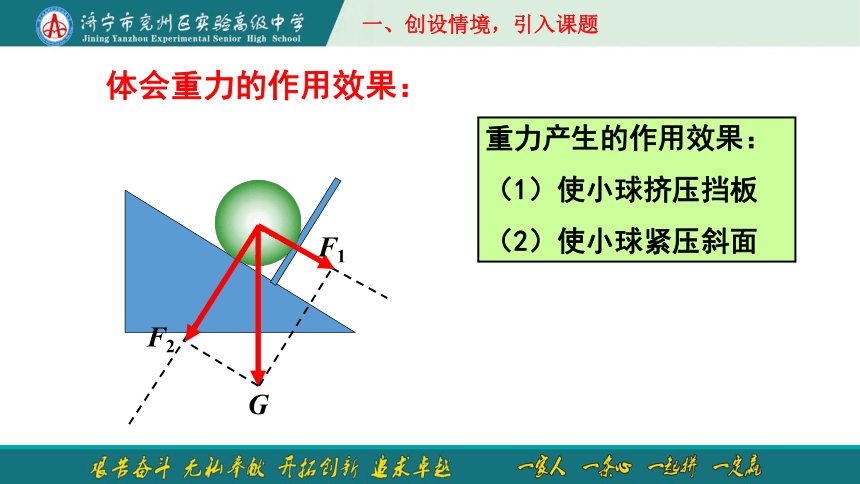
重力产生的作用效果:
(1)使小球挤压挡板
(2)使小球紧压斜面
体会重力的作用效果:
G
F2
F1
一、创设情境,引入课题
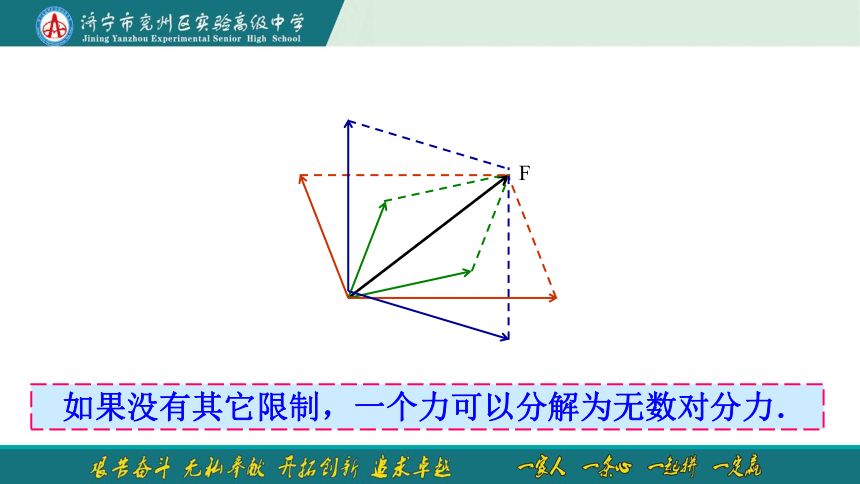
如果没有其它限制,一个力可以分解为无数对分力.
F
教学目标:
(1)理解平面向量基本定理及其意义。
(2)会运用平面向量基本定理解决简单平面几何问题。
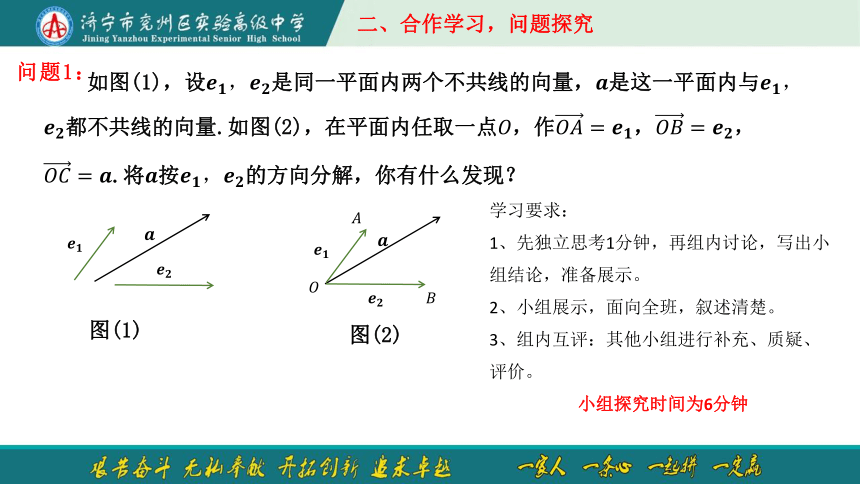
如图(1),设????????,????????是同一平面内两个不共线的向量,????是这一平面内与????????,????????都不共线的向量.如图(2),在平面内任取一点????,作????????=????????,????????=????????,????????=????.将????按????????,????????的方向分解,你有什么发现?
?
????????
?
????????
?
????
?
图(1)
????????
?
????????
?
????
?
????
?
????
?
????
?
图(2)
问题1:
二、合作学习,问题探究
学习要求:
1、先独立思考1分钟,再组内讨论,写出小组结论,准备展示。
2、小组展示,面向全班,叙述清楚。
3、组内互评:其他小组进行补充、质疑、评价。
小组探究时间为6分钟
O
C
A
B
M
N
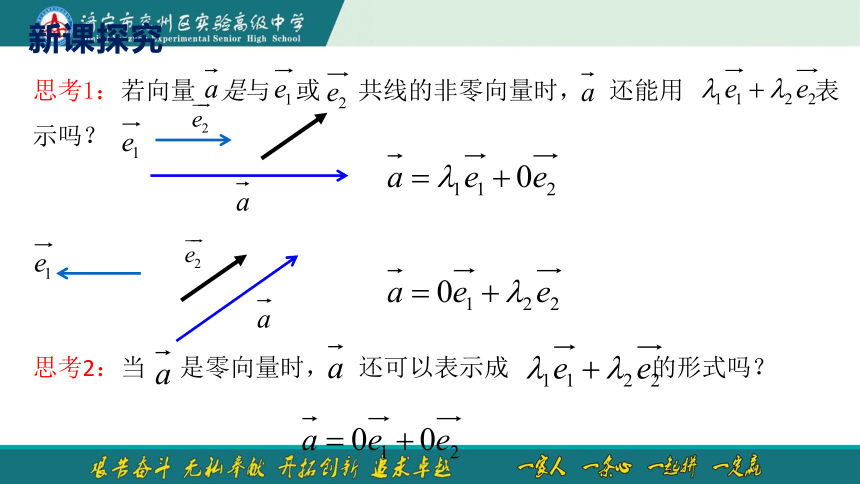
思考1:若向量 是与 或 共线的非零向量时, 还能用 表示吗?
思考2:当 是零向量时, 还可以表示成 的形式吗?
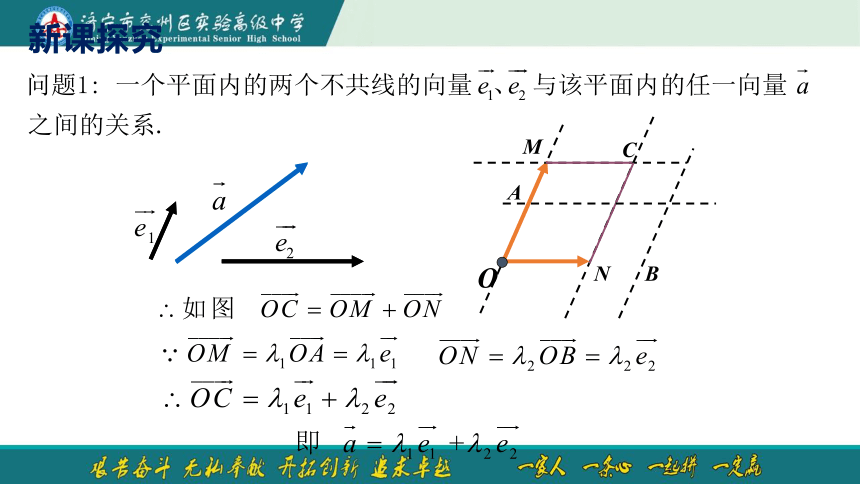
结论1:一般地,对给定不共线的向量?????????,???????????,任意一个向量????都可以表示成λ1?????????+λ2????????的形式.
?
思考3:平面内任一向量????都可以表示成λ1?????????+λ2????????(????????,????????不共线)的形式,这种表示形式是唯一的吗?
?
思考3:平面内任一向量????都可以表示成λ1?????????+λ2????????(????????,????????不共线)的形式,这种表示形式是唯一的吗?
?
若?????=?????????????????+?????????????????,则?????????????????+?????????????????=??????????????????+?????????????????.
得( λ1-?????????)?????????+( λ2 -?????????)?????????= ?????.
则λ1-?????????, λ2 -????????全为0
(假设λ1-μ1,λ2-μ2不全为0,不妨假设λ1-μ1≠0,
则????????=?????????????????????????????????? ????????,由此可得????????,????????共线,
与已知????????,????????不共线矛盾.)
即λ1=μ1,λ2=μ2。
?
任何一个向量都可以由同一个基底唯一表示
1.平面向量基本定理
.
注:1.平面内任意两个不共线向量都可以作为基底,一旦选定一组基底,则平面内的任意向量都可用该组基底唯一表示;
2.对于确定的基底????????,????????,
同一向量的分解式是唯一的,
不同向量的分解式是不同的,
同一非零向量在不同的基底下分解式是不同的,
零向量的分解式是唯一的。
?
1. 设e1,e2是同一平面内两个不共线的向量,以下各组向量中不能作为基底的是( )
A.{e1,e2} B.{e1+e2,3e1+3e2} C.{e1,5e2} D.{e1,e1+e2}
B
2. 已知平行四边形ABCD,两条对角线交于点O,则下列各组向量中,可以作为该平面内所有向量基底的是( )
CD
①基底不共线
②基底不唯一
题型一、用基底表示向量
所以
例1 如图, 不共线,且 ,用 表示 .
因为
解法二:
若A,B,P三点共线,O为直线外一点
归纳提升
三应用训练 拓展提升
题型一、用基底表示向量
如图,AD,BE,CF是△ABC的三条中线, ,用a,b表示
C
A
B
E
D
F
练习1
练习2已知向量e1、e2不共线,a=-e1+3e2,b=e1+2e2,c=-3e1+12e2,请用a,b表示c.
小结:
用基底表示向量的方法:
(1)运用向量的线性运算法则对待求向量不断进行转化,直至用基底表示为止
(2)通过列向量方程或方程组的形式,利用基底表示向量的唯一性求解.
题型二:平面向量基本定理在几何中的应用
例2如图,CD是△ABC的中线,且 CD= AB,用向量方法证明△ABC是直角三角形.
C
A
D
B
学习要求:
1、独立思考并在练习本上规范作答。
2、小组内成员进行展示交流。
3、班级整体进行展示。
时间限制为5分钟
题型二:平面向量基本定理在几何中的应用
例2如图,CD是△ABC的中线,且 CD= AB,用向量方法证明△ABC是直角三角形.
C
A
D
B
因为CD= AB,所以CD=DA.因为 ,
所以 .
因此CA⊥CB.结论成立.
证明:设
则
小结:用向量解决平面几何问题的一般步骤:
1.选基底
2.将相关向量用基底表示,将几何问题转化为向量问题;
3.进行向量运算,解决向量问题
4.再将向量问题转化为几何问题
通过本节课的学习,你学到了哪些知识?本节课在研究问题的过程中用到了哪些数学思想方法?
四、课堂小结,知识升华
1.知识点:
(1)平面向量基本定理.
(2)用基底表示向量.
(3)平面向量基本定理的应用.
2.方法归纳:数形结合法,待定系数法、反证法,
转化思想、方程思想
3.易错点:忽视基底中的向量必须是不共线的两个向量.
【第六章 平面向量及其应用】
6.3.1平面向量基本定理
重力产生的作用效果:
(1)使小球挤压挡板
(2)使小球紧压斜面
体会重力的作用效果:
G
F2
F1
一、创设情境,引入课题
如果没有其它限制,一个力可以分解为无数对分力.
F
教学目标:
(1)理解平面向量基本定理及其意义。
(2)会运用平面向量基本定理解决简单平面几何问题。
如图(1),设????????,????????是同一平面内两个不共线的向量,????是这一平面内与????????,????????都不共线的向量.如图(2),在平面内任取一点????,作????????=????????,????????=????????,????????=????.将????按????????,????????的方向分解,你有什么发现?
?
????????
?
????????
?
????
?
图(1)
????????
?
????????
?
????
?
????
?
????
?
????
?
图(2)
问题1:
二、合作学习,问题探究
学习要求:
1、先独立思考1分钟,再组内讨论,写出小组结论,准备展示。
2、小组展示,面向全班,叙述清楚。
3、组内互评:其他小组进行补充、质疑、评价。
小组探究时间为6分钟
O
C
A
B
M
N
思考1:若向量 是与 或 共线的非零向量时, 还能用 表示吗?
思考2:当 是零向量时, 还可以表示成 的形式吗?
结论1:一般地,对给定不共线的向量?????????,???????????,任意一个向量????都可以表示成λ1?????????+λ2????????的形式.
?
思考3:平面内任一向量????都可以表示成λ1?????????+λ2????????(????????,????????不共线)的形式,这种表示形式是唯一的吗?
?
思考3:平面内任一向量????都可以表示成λ1?????????+λ2????????(????????,????????不共线)的形式,这种表示形式是唯一的吗?
?
若?????=?????????????????+?????????????????,则?????????????????+?????????????????=??????????????????+?????????????????.
得( λ1-?????????)?????????+( λ2 -?????????)?????????= ?????.
则λ1-?????????, λ2 -????????全为0
(假设λ1-μ1,λ2-μ2不全为0,不妨假设λ1-μ1≠0,
则????????=?????????????????????????????????? ????????,由此可得????????,????????共线,
与已知????????,????????不共线矛盾.)
即λ1=μ1,λ2=μ2。
?
任何一个向量都可以由同一个基底唯一表示
1.平面向量基本定理
.
注:1.平面内任意两个不共线向量都可以作为基底,一旦选定一组基底,则平面内的任意向量都可用该组基底唯一表示;
2.对于确定的基底????????,????????,
同一向量的分解式是唯一的,
不同向量的分解式是不同的,
同一非零向量在不同的基底下分解式是不同的,
零向量的分解式是唯一的。
?
1. 设e1,e2是同一平面内两个不共线的向量,以下各组向量中不能作为基底的是( )
A.{e1,e2} B.{e1+e2,3e1+3e2} C.{e1,5e2} D.{e1,e1+e2}
B
2. 已知平行四边形ABCD,两条对角线交于点O,则下列各组向量中,可以作为该平面内所有向量基底的是( )
CD
①基底不共线
②基底不唯一
题型一、用基底表示向量
所以
例1 如图, 不共线,且 ,用 表示 .
因为
解法二:
若A,B,P三点共线,O为直线外一点
归纳提升
三应用训练 拓展提升
题型一、用基底表示向量
如图,AD,BE,CF是△ABC的三条中线, ,用a,b表示
C
A
B
E
D
F
练习1
练习2已知向量e1、e2不共线,a=-e1+3e2,b=e1+2e2,c=-3e1+12e2,请用a,b表示c.
小结:
用基底表示向量的方法:
(1)运用向量的线性运算法则对待求向量不断进行转化,直至用基底表示为止
(2)通过列向量方程或方程组的形式,利用基底表示向量的唯一性求解.
题型二:平面向量基本定理在几何中的应用
例2如图,CD是△ABC的中线,且 CD= AB,用向量方法证明△ABC是直角三角形.
C
A
D
B
学习要求:
1、独立思考并在练习本上规范作答。
2、小组内成员进行展示交流。
3、班级整体进行展示。
时间限制为5分钟
题型二:平面向量基本定理在几何中的应用
例2如图,CD是△ABC的中线,且 CD= AB,用向量方法证明△ABC是直角三角形.
C
A
D
B
因为CD= AB,所以CD=DA.因为 ,
所以 .
因此CA⊥CB.结论成立.
证明:设
则
小结:用向量解决平面几何问题的一般步骤:
1.选基底
2.将相关向量用基底表示,将几何问题转化为向量问题;
3.进行向量运算,解决向量问题
4.再将向量问题转化为几何问题
通过本节课的学习,你学到了哪些知识?本节课在研究问题的过程中用到了哪些数学思想方法?
四、课堂小结,知识升华
1.知识点:
(1)平面向量基本定理.
(2)用基底表示向量.
(3)平面向量基本定理的应用.
2.方法归纳:数形结合法,待定系数法、反证法,
转化思想、方程思想
3.易错点:忽视基底中的向量必须是不共线的两个向量.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
