8.3.3球的表面积和体积 课件(共20张PPT)
文档属性
| 名称 | 8.3.3球的表面积和体积 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-25 21:40:47 | ||
图片预览







文档简介
7.1.1 数系的扩充和复数的概念
2023/3/25
第八章 立体几何初步
8.3.2.2 球的表面积和体积
学习目标
1.知道球的表面积和体积的计算公式,能用公式解决简单的实际问题。
2.了解球的体积公式的推导过程,提高空间思维能力和空间想象能力。
3. 球的截面及其性质
① 用一个平面去截球,截面是圆面;
② 球心和截面圆心的连线与截面垂直,
与截面内的直线都垂直.
O1
R2 = r2 + d2
③ 球心到截面的距离d与球的半径R及截面的半径r的关系:
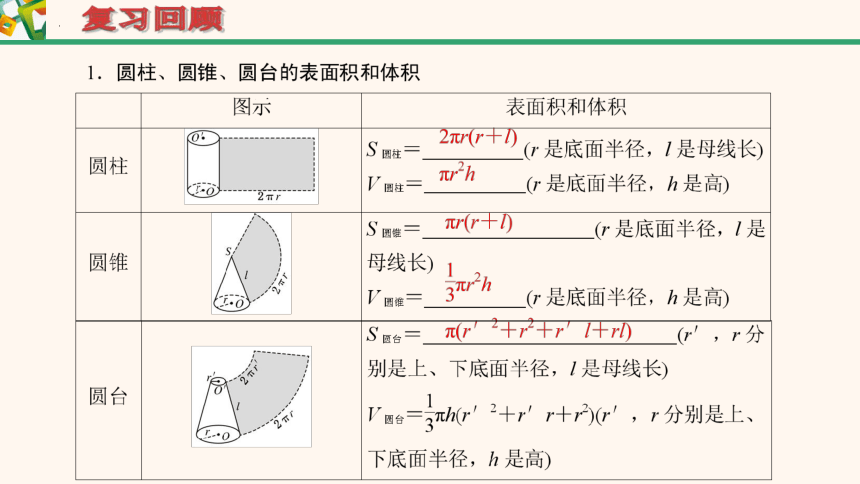
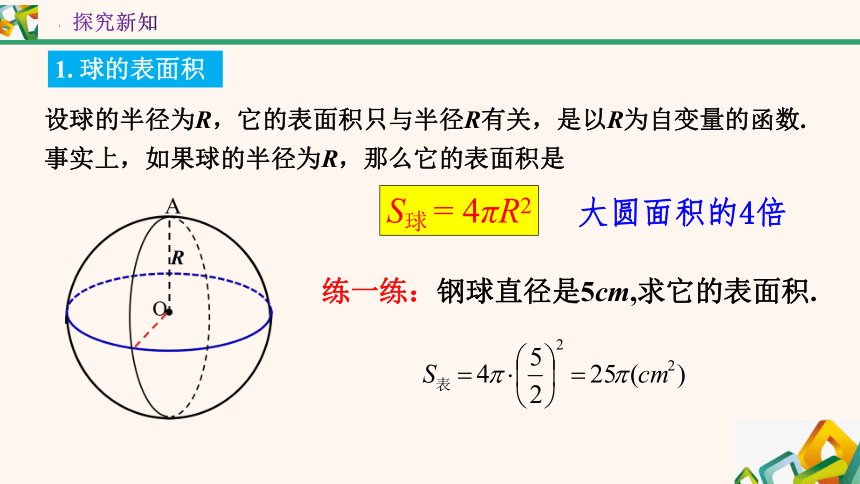
1. 球的表面积
设球的半径为R,它的表面积只与半径R有关,是以R为自变量的函数.事实上,如果球的半径为R,那么它的表面积是
S球 = 4πR2
大圆面积的4倍
练一练:钢球直径是5cm,求它的表面积.
探究新知
例1 如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(π取3.14)
解:一个浮标的表面积为
2π×0.15×0.6+4π×0.152=0.8478(m2),
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000=423.9(kg).
例题讲解
圆的面积公式的推导
分割
以直代曲
取极限
……
n=6
A3
An
A4
作圆的内接正六,十二边形,…
思想方法:
思考:在小学,我们学习了圆的面积公式,你知道这个公式是如何推出的吗?
是谁想出来这种方法的呢?
n=12
球的体积公式的推导
第一步:分割
将球O 的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥体”.
第二步:以直代曲
当n 越大时,每个小网格就越小,每个“小锥体”的底面就越平,“小锥体”就越近似于棱锥,棱锥的高近似于球半径R.
设O-ABCD是其中一个“小锥体”,则它的体积是
第三步:取极限
由于球的体积是这n个“小锥体”的体积之和,而这n个“小锥体”的底面积之和就是球的表面积,
当n趋于无穷大时,球的体积为:
分割
以直代曲
取极限
思想方法:
思考 类比圆的面积公式的推导方法,你能推导出球的体积公式?
例2 一平面截一球得到直径为2????cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是 ( )
A.12π cm3 B.36π cm3 C.64π cm3 D.108π cm3
?
例题讲解
练习 如图示,圆柱的底面直径和高都等于球的直径, 求球与圆柱的体积之比.
解:设球的半径为R,则圆柱的底面半径也为R,高为2R.
即球与圆柱的体积之比为2:3.
例题讲解
外接球:将几何体包围,且几何体的顶点和弧面在此球上
内切球:球体在几何体里面,且球体与几何体每个面均相切。
棱切球:球体与几何体每条棱均相切。
外接球
外接球
内切球
棱切球
球的接与切
探究新知
长方体的外接球
结论:长方体外接球的直径等于长方体的体对角线.
(2R)2=a2+b2+c2(a,b,c是长方体的棱长)
解:
作出截面图如图示.
由图可知,球的直径等于正方体的体对角线长,即
∴ 球的表面积为
14π
结论:正方体外接球直径等于正方体的(体)对角线的长
课堂练习
结论:正方体棱切球的球的直径等于一个面上的对角线长
例题讲解
O
?
A
解:
作出截面图如图示.
由图可知,
球的直径等于正方体的棱长,
即
2R = 2,∴R = 1.
∴ 球的体积为
正方体的内切球
结论:正方体内切球的直径等于正方体棱长。
切点:各个面的中心.
球心:正方体的中心.
直径:相对两个面中心连线.
直径等于正方体的棱长.
①内切球
?
O
O
?
②棱切球
O
?
?
O
切点:各棱的中点.
球心:正方体的中心.
直径: “对棱”中点连线
直径等于正方体一个面的对角线长.
③外接球
O
A
B
C
D
O
?
A
B
C
D
直径等于正方体的体对角线长.
球心:正方体的中心.
直径: 体对角线
归纳总结
直棱柱外接球
?
O
?
O2
C
B
A
a
?
O1
B
AO2=
∴R2=AO2=AO22+OO22=
OO2=
∴S球=4πR2=
课堂小结
?
O
R
1.球的表面积、体积公式
2. 球与多面体的内切、外接
3. 思想方法:
1.长方体的外接球
2.正方体的三个球
(2R)2=a2+b2+c2
分割
以直代曲
取极限
PPT模板下载:www.1ppt.com/moban/ 行业PPT模板:www.1ppt.com/hangye/
节日PPT模板:www.1ppt.com/jieri/ PPT素材下载:www.1ppt.com/sucai/
PPT背景图片:www.1ppt.com/beijing/ PPT图表下载:www.1ppt.com/tubiao/
优秀PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
Word教程: www.1ppt.com/word/ Excel教程:www.1ppt.com/excel/
资料下载:www.1ppt.com/ziliao/ PPT课件下载:www.1ppt.com/kejian/
范文下载:www.1ppt.com/fanwen/ 试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/ PPT论坛:www.1ppt.cn
Thank you
感谢聆听
2023/3/25
第八章 立体几何初步
8.3.2.2 球的表面积和体积
学习目标
1.知道球的表面积和体积的计算公式,能用公式解决简单的实际问题。
2.了解球的体积公式的推导过程,提高空间思维能力和空间想象能力。
3. 球的截面及其性质
① 用一个平面去截球,截面是圆面;
② 球心和截面圆心的连线与截面垂直,
与截面内的直线都垂直.
O1
R2 = r2 + d2
③ 球心到截面的距离d与球的半径R及截面的半径r的关系:
1. 球的表面积
设球的半径为R,它的表面积只与半径R有关,是以R为自变量的函数.事实上,如果球的半径为R,那么它的表面积是
S球 = 4πR2
大圆面积的4倍
练一练:钢球直径是5cm,求它的表面积.
探究新知
例1 如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(π取3.14)
解:一个浮标的表面积为
2π×0.15×0.6+4π×0.152=0.8478(m2),
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000=423.9(kg).
例题讲解
圆的面积公式的推导
分割
以直代曲
取极限
……
n=6
A3
An
A4
作圆的内接正六,十二边形,…
思想方法:
思考:在小学,我们学习了圆的面积公式,你知道这个公式是如何推出的吗?
是谁想出来这种方法的呢?
n=12
球的体积公式的推导
第一步:分割
将球O 的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥体”.
第二步:以直代曲
当n 越大时,每个小网格就越小,每个“小锥体”的底面就越平,“小锥体”就越近似于棱锥,棱锥的高近似于球半径R.
设O-ABCD是其中一个“小锥体”,则它的体积是
第三步:取极限
由于球的体积是这n个“小锥体”的体积之和,而这n个“小锥体”的底面积之和就是球的表面积,
当n趋于无穷大时,球的体积为:
分割
以直代曲
取极限
思想方法:
思考 类比圆的面积公式的推导方法,你能推导出球的体积公式?
例2 一平面截一球得到直径为2????cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是 ( )
A.12π cm3 B.36π cm3 C.64π cm3 D.108π cm3
?
例题讲解
练习 如图示,圆柱的底面直径和高都等于球的直径, 求球与圆柱的体积之比.
解:设球的半径为R,则圆柱的底面半径也为R,高为2R.
即球与圆柱的体积之比为2:3.
例题讲解
外接球:将几何体包围,且几何体的顶点和弧面在此球上
内切球:球体在几何体里面,且球体与几何体每个面均相切。
棱切球:球体与几何体每条棱均相切。
外接球
外接球
内切球
棱切球
球的接与切
探究新知
长方体的外接球
结论:长方体外接球的直径等于长方体的体对角线.
(2R)2=a2+b2+c2(a,b,c是长方体的棱长)
解:
作出截面图如图示.
由图可知,球的直径等于正方体的体对角线长,即
∴ 球的表面积为
14π
结论:正方体外接球直径等于正方体的(体)对角线的长
课堂练习
结论:正方体棱切球的球的直径等于一个面上的对角线长
例题讲解
O
?
A
解:
作出截面图如图示.
由图可知,
球的直径等于正方体的棱长,
即
2R = 2,∴R = 1.
∴ 球的体积为
正方体的内切球
结论:正方体内切球的直径等于正方体棱长。
切点:各个面的中心.
球心:正方体的中心.
直径:相对两个面中心连线.
直径等于正方体的棱长.
①内切球
?
O
O
?
②棱切球
O
?
?
O
切点:各棱的中点.
球心:正方体的中心.
直径: “对棱”中点连线
直径等于正方体一个面的对角线长.
③外接球
O
A
B
C
D
O
?
A
B
C
D
直径等于正方体的体对角线长.
球心:正方体的中心.
直径: 体对角线
归纳总结
直棱柱外接球
?
O
?
O2
C
B
A
a
?
O1
B
AO2=
∴R2=AO2=AO22+OO22=
OO2=
∴S球=4πR2=
课堂小结
?
O
R
1.球的表面积、体积公式
2. 球与多面体的内切、外接
3. 思想方法:
1.长方体的外接球
2.正方体的三个球
(2R)2=a2+b2+c2
分割
以直代曲
取极限
PPT模板下载:www.1ppt.com/moban/ 行业PPT模板:www.1ppt.com/hangye/
节日PPT模板:www.1ppt.com/jieri/ PPT素材下载:www.1ppt.com/sucai/
PPT背景图片:www.1ppt.com/beijing/ PPT图表下载:www.1ppt.com/tubiao/
优秀PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
Word教程: www.1ppt.com/word/ Excel教程:www.1ppt.com/excel/
资料下载:www.1ppt.com/ziliao/ PPT课件下载:www.1ppt.com/kejian/
范文下载:www.1ppt.com/fanwen/ 试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/ PPT论坛:www.1ppt.cn
Thank you
感谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
