11.4 多项式乘多项式课件
图片预览



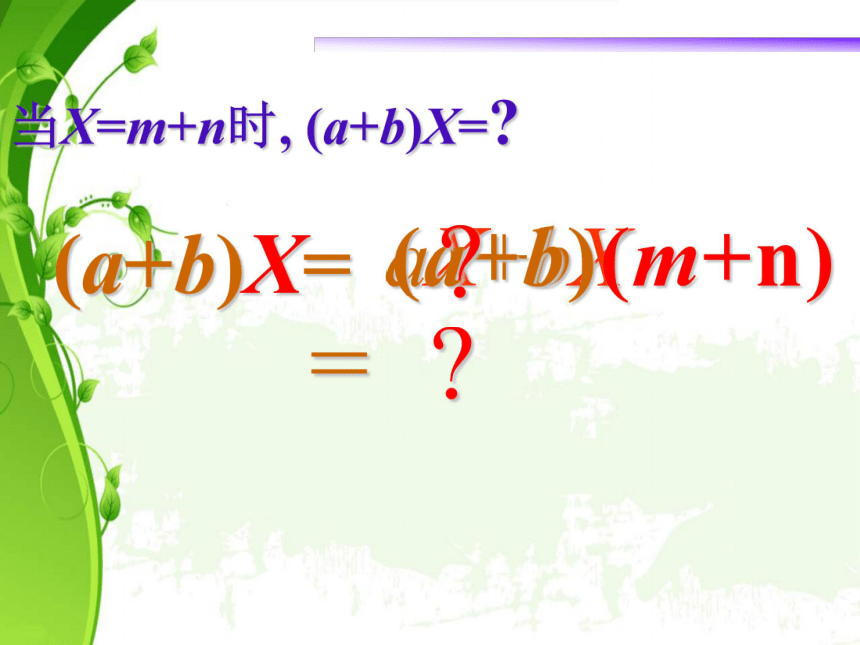


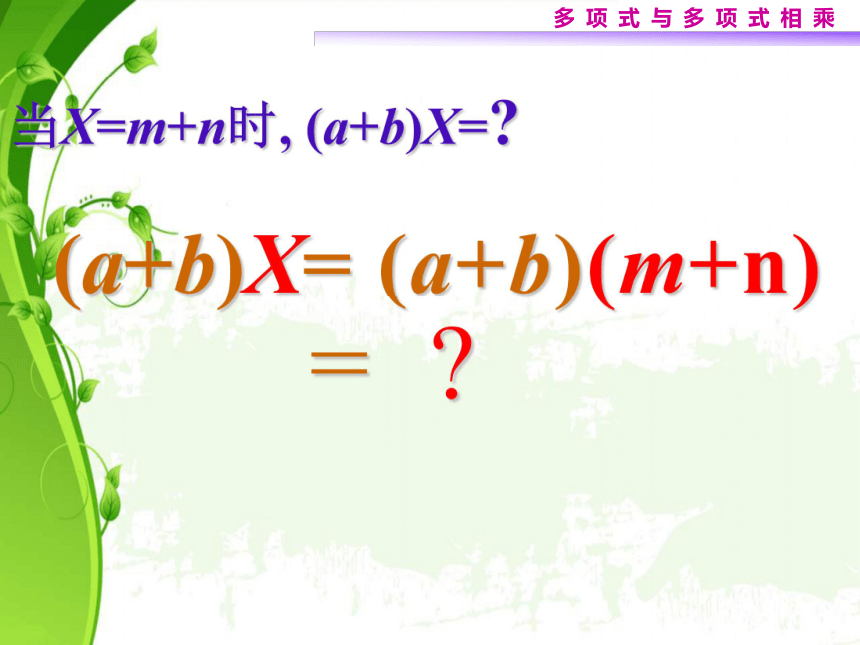
文档简介
课件23张PPT。多项式乘以多项式预习提纲1、多项式与多项式相乘的法则是什么?
依据是什么?
2、多项式与多项式相乘,结果的项数与原 多项式的项数有何关系?
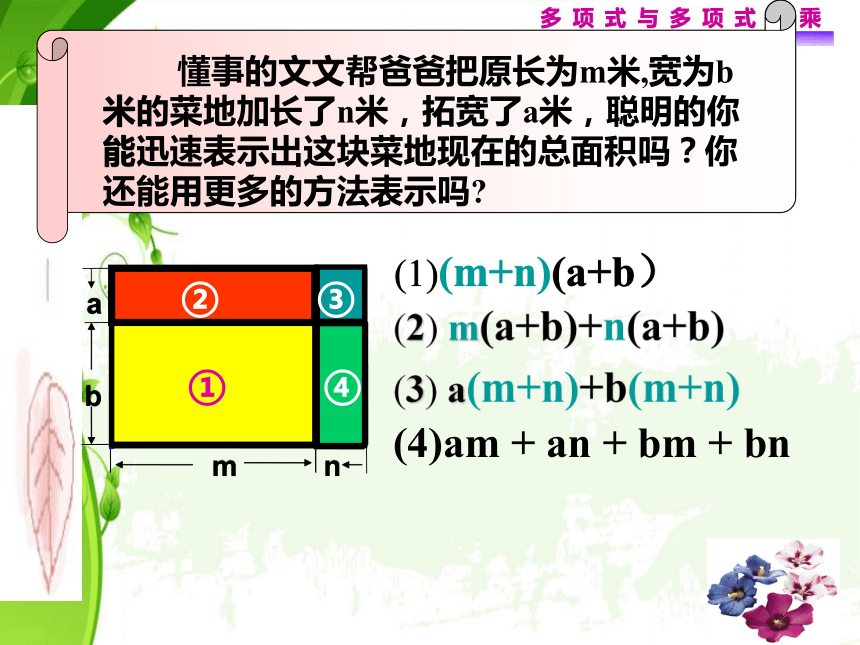
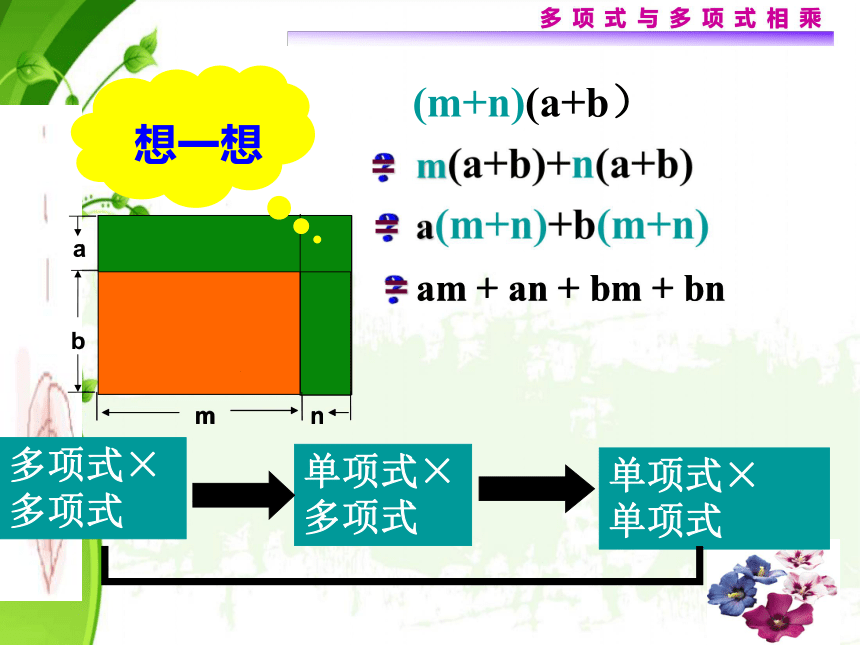
3、积的每一项的符号由谁决定?练习 可要认真!(a+b)X=aX+bX当X=m+n时, (a+b)X=?(a+b)(m+n)=??多项式与多项式相乘bmna(4)am + an + bm + bn①②③④多项式与多项式相乘am + an + bm + bnbmna多项式×
多项式单项式×
多项式单项式×
单项式(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则:(a+b)(m+n)=am+an+bm+bn多项式与多项式相乘(a+b)X=当X=m+n时, (a+b)X=?(a+b)(m+n)=?多项式与多项式相乘计算:直接利用:多项式乘以多项式的法则多项式与多项式相乘例题解析 【例4】计算: (1)(x+2)(x?3) (2)(3x -1)(2x+1)=x2 -x-6 (2) (3x -1)(2x+1)=6x2+3x-2 x?1=6x2 +x?1=计算:(1) (3x+2y)( x-5y)
(2)(x+y)(x2-xy+y2)
(3)(x+2)(x+4)-x(x+1)-8
(4)3(x-2)(x+1)-2(x-5)(x-3)多项式与多项式相乘计算:再显身手判别下列解法是否正确,若错请说出理由。判别下列解法是否正确,若错请说出理由。解:原式运算结果不是最简形式 【例3】 计算:
x(x2+3)+x2(x-3)-3x(x2-x-1). 错解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x-3x3+3x2+3x. 剖析:本题在运用法则运算时并没有错,问题出在其结果没有合并同类项. 正解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x2-3x3+3x2+3x=-x3+6x. . 四、顺序混乱 【例4】计算:(a+2)(3-a). 错解:(a+2)(3-a)=3a-2a+a2+6=a2+a+6. 分析:此题错解中,一是有符号错误,误将“-”写成“+”;二是方法不当,是指这里计算顺序混乱,这样容易出错.应根据多项式的乘法法则计算. 正解:(a+2)(3-a)=3a-a2+6-2a=-a2+a+6解方程:
(1)(2x+3)(x-4)-(x+2)(x-2)=x2+7
(2) (3x-2)(2x-3)=(6x+5)(x-1)-1 【例4】阅读下列解答过程,并回答问题:在(x2+ax+b)(2x2-3x-1)的积中,x3的系数为
-5,x2的系数为-6,求a、b. 解:(x2+ax+b)(2x2-3x-1) =2x4-3x3+2ax3-3ax2+2bx2-3bx ① =2x 4-(3-2a)x 3-(3a-2b)x 2-3bx ②
根据对应项系数相等,有解得回答:(1)上述解答过程是否正确?(2)若不正确,从第___步开始出错的,其他步骤是否还有错误? (3)写出正确的解答过程:_____.
计算:
1.(1)(3x-2y)(2x+3y)
(2)(x+2)(x+3)-(x+6)(x-1)
(3)(3x2+2x+1)(2x2+3x-1)
(4)(3x+2y)(2x+3y)-(x-3y)(3x+4y)
2.已知多项式(mx+8)(2-3x)展开后不含x项,求m的值延伸训练:填空:观察上面四个等式,你能发现什么规律?5 61 (-6)(-1) (-6)(-5) 6延伸训练:你能根据这个规律解决下面的问题吗?比一比:学了这节课,你有什么收获? 说一说:多项式与多项式相乘
依据是什么?
2、多项式与多项式相乘,结果的项数与原 多项式的项数有何关系?
3、积的每一项的符号由谁决定?练习 可要认真!(a+b)X=aX+bX当X=m+n时, (a+b)X=?(a+b)(m+n)=??多项式与多项式相乘bmna(4)am + an + bm + bn①②③④多项式与多项式相乘am + an + bm + bnbmna多项式×
多项式单项式×
多项式单项式×
单项式(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则:(a+b)(m+n)=am+an+bm+bn多项式与多项式相乘(a+b)X=当X=m+n时, (a+b)X=?(a+b)(m+n)=?多项式与多项式相乘计算:直接利用:多项式乘以多项式的法则多项式与多项式相乘例题解析 【例4】计算: (1)(x+2)(x?3) (2)(3x -1)(2x+1)=x2 -x-6 (2) (3x -1)(2x+1)=6x2+3x-2 x?1=6x2 +x?1=计算:(1) (3x+2y)( x-5y)
(2)(x+y)(x2-xy+y2)
(3)(x+2)(x+4)-x(x+1)-8
(4)3(x-2)(x+1)-2(x-5)(x-3)多项式与多项式相乘计算:再显身手判别下列解法是否正确,若错请说出理由。判别下列解法是否正确,若错请说出理由。解:原式运算结果不是最简形式 【例3】 计算:
x(x2+3)+x2(x-3)-3x(x2-x-1). 错解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x-3x3+3x2+3x. 剖析:本题在运用法则运算时并没有错,问题出在其结果没有合并同类项. 正解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x2-3x3+3x2+3x=-x3+6x. . 四、顺序混乱 【例4】计算:(a+2)(3-a). 错解:(a+2)(3-a)=3a-2a+a2+6=a2+a+6. 分析:此题错解中,一是有符号错误,误将“-”写成“+”;二是方法不当,是指这里计算顺序混乱,这样容易出错.应根据多项式的乘法法则计算. 正解:(a+2)(3-a)=3a-a2+6-2a=-a2+a+6解方程:
(1)(2x+3)(x-4)-(x+2)(x-2)=x2+7
(2) (3x-2)(2x-3)=(6x+5)(x-1)-1 【例4】阅读下列解答过程,并回答问题:在(x2+ax+b)(2x2-3x-1)的积中,x3的系数为
-5,x2的系数为-6,求a、b. 解:(x2+ax+b)(2x2-3x-1) =2x4-3x3+2ax3-3ax2+2bx2-3bx ① =2x 4-(3-2a)x 3-(3a-2b)x 2-3bx ②
根据对应项系数相等,有解得回答:(1)上述解答过程是否正确?(2)若不正确,从第___步开始出错的,其他步骤是否还有错误? (3)写出正确的解答过程:_____.
计算:
1.(1)(3x-2y)(2x+3y)
(2)(x+2)(x+3)-(x+6)(x-1)
(3)(3x2+2x+1)(2x2+3x-1)
(4)(3x+2y)(2x+3y)-(x-3y)(3x+4y)
2.已知多项式(mx+8)(2-3x)展开后不含x项,求m的值延伸训练:填空:观察上面四个等式,你能发现什么规律?5 61 (-6)(-1) (-6)(-5) 6延伸训练:你能根据这个规律解决下面的问题吗?比一比:学了这节课,你有什么收获? 说一说:多项式与多项式相乘
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
