20.1.3加权平均数 学案
图片预览



文档简介
中小学教育资源及组卷应用平台
20.1.3加权平均数 导学案
课题 20.1.3加权平均数 单元 第20单元 学科 数学 年级 八年级(下)
教材分析 创设情境为权的产生提供背景,引导学生理解权的重要性,了解加权平均数的意义和优越性. 通过探索了解“权”的差异对平均数的影响,发现算术平均数和加权平均数的关系. 为后续从多角度体会中位教、众数与平均数的差别作为参考,提供工平台.
核心素养分析 了解加权平均数的意义和优越性. 利用算术平均数和加权平均数解决实际问题,增强统计意识和数学应用的能力. 了解数学的价值,加深数学的理解和学好数学的信心.
学习目标 1.掌握加权平均数的概念,会求一组数据的加权平均数. 2.会用加权平均数解决实际生活中的问题.
重点 掌握加权平均数的计算方法;运用加权平均数解决实际问题.
难点 探索算术平均数和加权平均数的联系和区别.
教学过程
课前预学 引入思考思考1.商店里有两种苹果,一种单价为3.50元千克,另一种单价为6元千克.小明妈妈买了单价为3.50元千克的苹果1千克,单价为6元千克的苹果3千克,那么小明妈妈所买苹果的平均价格是两个单价相加除以2吗 为什么 思考2.老师在计算学生每学期的总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2,而是按照“平时成绩占40%,考试成绩占60%”的比例计算(如图所示) ,其中考试成绩更为重要,这样,如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩是多少 问题探究:小明同学的期中考试各科成绩分别为:语文96分,数学92分,英语88分,那么他的平均成绩为多少? 即每个数据都乘与1,和不乘之前值都是一样的,那么它是不是没有一点意义啊。其实,这个1就是每个数据的“权”,在每一个数的权数相同的情况下,加权平均值就等于算数平均值。方案设计:语文、数学、英语的“重要程度”分别按1:1:1时其实它就是算术平均数(算术平均数其实就是一个特殊的加权平均数,其权重都相等。)语文、数学、英语的“重要程度”分别按40%、40%、20%的比例计算期中成绩。(或将比例改成4 :4 :2)语文、数学、英语的“重要程度”分别按50%、30%、20%的比例计算期中成绩。(或将比例改成5 :3 :2)通过教师演示计算过程,让学生感知当为三项成绩设置一定的重要程度可以合理评定学生的学期成绩,体会4 :4 :2在计算中的过渡作用,利用5 :3 :2提出计算形式的转换需要,在讲解中不知不觉给出加权平均数的计算公式,体现公式的优越性。4、如果你是老师,你会按怎样的比例计算小明的学期成绩?5、如果你是小明,你希望老师按怎样的比例计算你的期中成绩?(4、5小题请学生给定比例,说明理由,并选择其中2、3个进行计算)思考:为什么相同的三项成绩产生不同的的期中成绩?是什么在起作用?归纳:加权平均数: 。计算公式:一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则 .
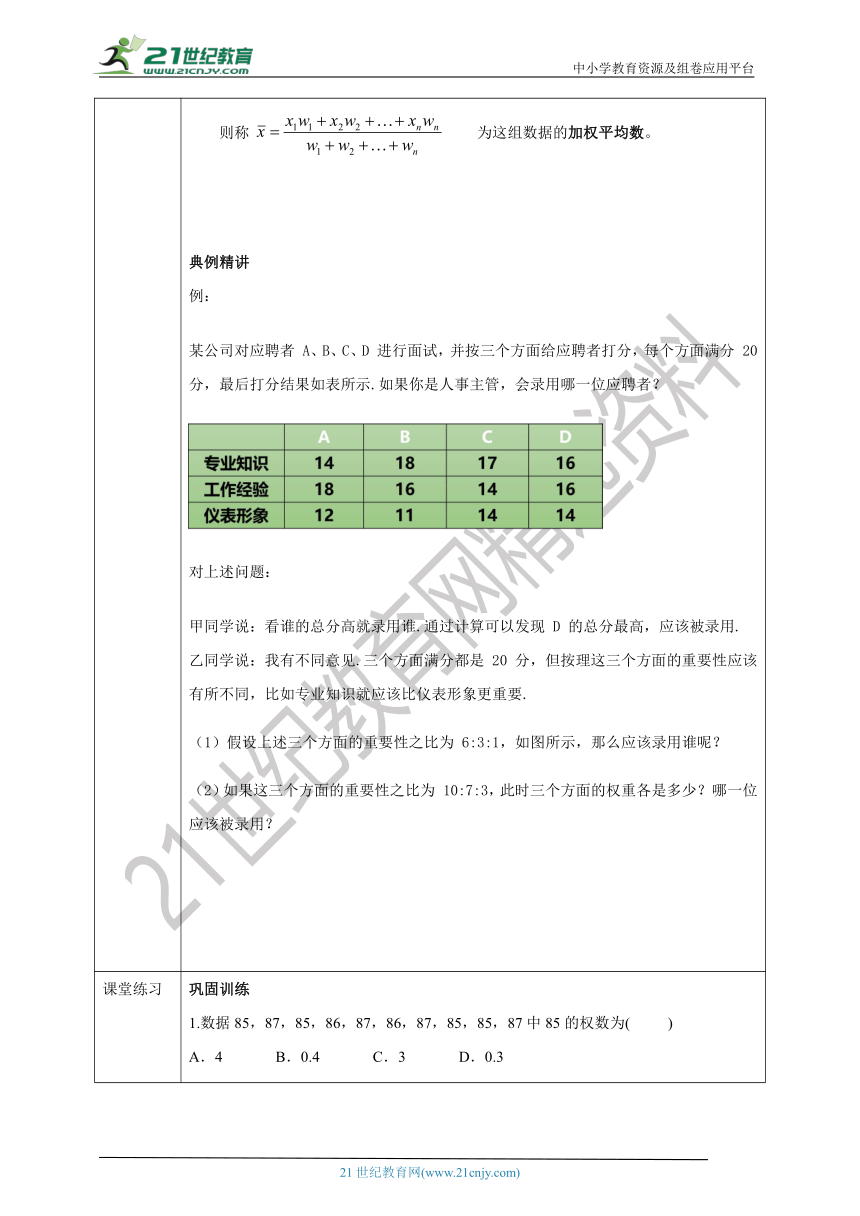
新知讲解 提炼概念一般地, 设x1,x2,…,xn为n个数据,w1,w2,…,wn依次为这n个数据的权数,则称 为这组数据的加权平均数。典例精讲 例:某公司对应聘者 A、B、C、D 进行面试,并按三个方面给应聘者打分,每个方面满分 20 分,最后打分结果如表所示.如果你是人事主管,会录用哪一位应聘者?对上述问题:甲同学说:看谁的总分高就录用谁.通过计算可以发现 D 的总分最高,应该被录用.乙同学说:我有不同意见.三个方面满分都是 20 分,但按理这三个方面的重要性应该有所不同,比如专业知识就应该比仪表形象更重要.(1)假设上述三个方面的重要性之比为 6:3:1,如图所示,那么应该录用谁呢?(2)如果这三个方面的重要性之比为 10:7:3,此时三个方面的权重各是多少?哪一位应该被录用?
课堂练习 巩固训练1.数据85,87,85,86,87,86,87,85,85,87中85的权数为( )A.4 B.0.4 C.3 D.0.33. 某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).解:这个跳水队运动员的平均年龄为: 4.某公司招聘活动中两位应试者的听、说、读、写成绩如下表:(1)假如你是这家公司的一名主管,想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩.从他们的成绩看,应该录取谁?(2)如果想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩(百分制).应该录取谁?5. 一家小吃店原有三个品种的馄饨,其中菜馅馄饨的售价为 3 元/ 碗,鸡蛋馅馄饨的售价为4元/碗,肉馅馄饨的售价为5元/碗.每碗均有10个馄饨.该店老板准备推出混合馄饨,请帮她解决以下问题:(1)如果每碗有3个菜馅的、3个鸡蛋馅的、4个肉馅的馄饨,那么混合馄饨每碗的定价应是多少 (2)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为3∶2∶5,那么混合馄饨每碗的定价应是多少 (3)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为1∶1∶3,那么混合馄饨每碗的定价应是多少 答案引入思考思考2 解:该同学的学期总评成绩是:70×40%+90×60%=82(分)40%,60%是权,82就是加权平均数在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.提炼概念典例精讲 例:(1)∵6:3:1=60%:30%:10%,∴专业知识、工作经验与仪表形象这三个方面的权重分别是 60%、30% 与 10%.(2)巩固训练 B2. C3. 4.(1)(2)解:(1)由题知,每碗中馄饨有十个,菜馅、鸡蛋馅、肉馅馄饨每碗分别为3元、4元、5元则菜馅、鸡蛋馅、肉馅馄饨每个分别为0.3元、0.4元、0.5元如果每碗有3个菜馅的、3个鸡蛋馅的、4个肉馅的馄饨,则定价应为:0.3×3+0.4×3+0.5×4=4.1(元)(2)解:如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为3∶2∶5,则一碗混合馄饨中菜馅、鸡蛋馅、肉馅馄饨所占比重为30%、20%、50%则每碗的定价为:3×30%+4×20%+5×50%=4.2(元)(3)解:如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为1∶1∶3,则一碗混合馄饨中菜馅、鸡蛋馅、肉馅馄饨所占比重为20%、20%、60%则每碗的定价为:3×20%+4×20%+5×60%=4.4(元)
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
20.1.3加权平均数 导学案
课题 20.1.3加权平均数 单元 第20单元 学科 数学 年级 八年级(下)
教材分析 创设情境为权的产生提供背景,引导学生理解权的重要性,了解加权平均数的意义和优越性. 通过探索了解“权”的差异对平均数的影响,发现算术平均数和加权平均数的关系. 为后续从多角度体会中位教、众数与平均数的差别作为参考,提供工平台.
核心素养分析 了解加权平均数的意义和优越性. 利用算术平均数和加权平均数解决实际问题,增强统计意识和数学应用的能力. 了解数学的价值,加深数学的理解和学好数学的信心.
学习目标 1.掌握加权平均数的概念,会求一组数据的加权平均数. 2.会用加权平均数解决实际生活中的问题.
重点 掌握加权平均数的计算方法;运用加权平均数解决实际问题.
难点 探索算术平均数和加权平均数的联系和区别.
教学过程
课前预学 引入思考思考1.商店里有两种苹果,一种单价为3.50元千克,另一种单价为6元千克.小明妈妈买了单价为3.50元千克的苹果1千克,单价为6元千克的苹果3千克,那么小明妈妈所买苹果的平均价格是两个单价相加除以2吗 为什么 思考2.老师在计算学生每学期的总评成绩时,并不是简单地将一个学生的平时成绩与考试成绩相加除以2,而是按照“平时成绩占40%,考试成绩占60%”的比例计算(如图所示) ,其中考试成绩更为重要,这样,如果一个学生的平时成绩为70分,考试成绩为90分,那么他的学期总评成绩是多少 问题探究:小明同学的期中考试各科成绩分别为:语文96分,数学92分,英语88分,那么他的平均成绩为多少? 即每个数据都乘与1,和不乘之前值都是一样的,那么它是不是没有一点意义啊。其实,这个1就是每个数据的“权”,在每一个数的权数相同的情况下,加权平均值就等于算数平均值。方案设计:语文、数学、英语的“重要程度”分别按1:1:1时其实它就是算术平均数(算术平均数其实就是一个特殊的加权平均数,其权重都相等。)语文、数学、英语的“重要程度”分别按40%、40%、20%的比例计算期中成绩。(或将比例改成4 :4 :2)语文、数学、英语的“重要程度”分别按50%、30%、20%的比例计算期中成绩。(或将比例改成5 :3 :2)通过教师演示计算过程,让学生感知当为三项成绩设置一定的重要程度可以合理评定学生的学期成绩,体会4 :4 :2在计算中的过渡作用,利用5 :3 :2提出计算形式的转换需要,在讲解中不知不觉给出加权平均数的计算公式,体现公式的优越性。4、如果你是老师,你会按怎样的比例计算小明的学期成绩?5、如果你是小明,你希望老师按怎样的比例计算你的期中成绩?(4、5小题请学生给定比例,说明理由,并选择其中2、3个进行计算)思考:为什么相同的三项成绩产生不同的的期中成绩?是什么在起作用?归纳:加权平均数: 。计算公式:一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则 .
新知讲解 提炼概念一般地, 设x1,x2,…,xn为n个数据,w1,w2,…,wn依次为这n个数据的权数,则称 为这组数据的加权平均数。典例精讲 例:某公司对应聘者 A、B、C、D 进行面试,并按三个方面给应聘者打分,每个方面满分 20 分,最后打分结果如表所示.如果你是人事主管,会录用哪一位应聘者?对上述问题:甲同学说:看谁的总分高就录用谁.通过计算可以发现 D 的总分最高,应该被录用.乙同学说:我有不同意见.三个方面满分都是 20 分,但按理这三个方面的重要性应该有所不同,比如专业知识就应该比仪表形象更重要.(1)假设上述三个方面的重要性之比为 6:3:1,如图所示,那么应该录用谁呢?(2)如果这三个方面的重要性之比为 10:7:3,此时三个方面的权重各是多少?哪一位应该被录用?
课堂练习 巩固训练1.数据85,87,85,86,87,86,87,85,85,87中85的权数为( )A.4 B.0.4 C.3 D.0.33. 某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).解:这个跳水队运动员的平均年龄为: 4.某公司招聘活动中两位应试者的听、说、读、写成绩如下表:(1)假如你是这家公司的一名主管,想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩.从他们的成绩看,应该录取谁?(2)如果想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩(百分制).应该录取谁?5. 一家小吃店原有三个品种的馄饨,其中菜馅馄饨的售价为 3 元/ 碗,鸡蛋馅馄饨的售价为4元/碗,肉馅馄饨的售价为5元/碗.每碗均有10个馄饨.该店老板准备推出混合馄饨,请帮她解决以下问题:(1)如果每碗有3个菜馅的、3个鸡蛋馅的、4个肉馅的馄饨,那么混合馄饨每碗的定价应是多少 (2)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为3∶2∶5,那么混合馄饨每碗的定价应是多少 (3)如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为1∶1∶3,那么混合馄饨每碗的定价应是多少 答案引入思考思考2 解:该同学的学期总评成绩是:70×40%+90×60%=82(分)40%,60%是权,82就是加权平均数在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.提炼概念典例精讲 例:(1)∵6:3:1=60%:30%:10%,∴专业知识、工作经验与仪表形象这三个方面的权重分别是 60%、30% 与 10%.(2)巩固训练 B2. C3. 4.(1)(2)解:(1)由题知,每碗中馄饨有十个,菜馅、鸡蛋馅、肉馅馄饨每碗分别为3元、4元、5元则菜馅、鸡蛋馅、肉馅馄饨每个分别为0.3元、0.4元、0.5元如果每碗有3个菜馅的、3个鸡蛋馅的、4个肉馅的馄饨,则定价应为:0.3×3+0.4×3+0.5×4=4.1(元)(2)解:如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为3∶2∶5,则一碗混合馄饨中菜馅、鸡蛋馅、肉馅馄饨所占比重为30%、20%、50%则每碗的定价为:3×30%+4×20%+5×50%=4.2(元)(3)解:如果菜馅、鸡蛋馅、肉馅馄饨的个数之比为1∶1∶3,则一碗混合馄饨中菜馅、鸡蛋馅、肉馅馄饨所占比重为20%、20%、60%则每碗的定价为:3×20%+4×20%+5×60%=4.4(元)
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
