人教版八年级下册18.2.1矩形 课件(共43张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.1矩形 课件(共43张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 633.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 17:02:51 | ||
图片预览







文档简介
(共43张PPT)
特殊的平行四边形
18.2.1 矩形
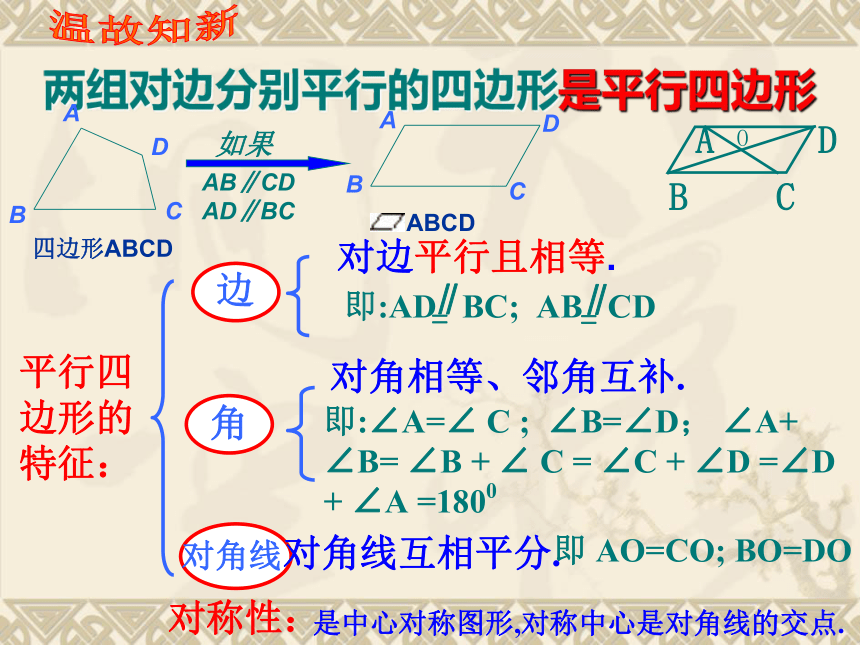
对边平行且相等.
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
平行四边形的特征:
边
角
对角线
温故知新
D
B
A
C
即:AD BC; AB CD
∥
=
∥
=
对角相等、邻角互补.
即:∠A=∠ C ; ∠B=∠D; ∠A+ ∠B= ∠B + ∠ C = ∠C + ∠D =∠D + ∠A =1800
对角线互相平分.
即 AO=CO; BO=DO
对称性:
是中心对称图形,对称中心是对角线的交点.
O
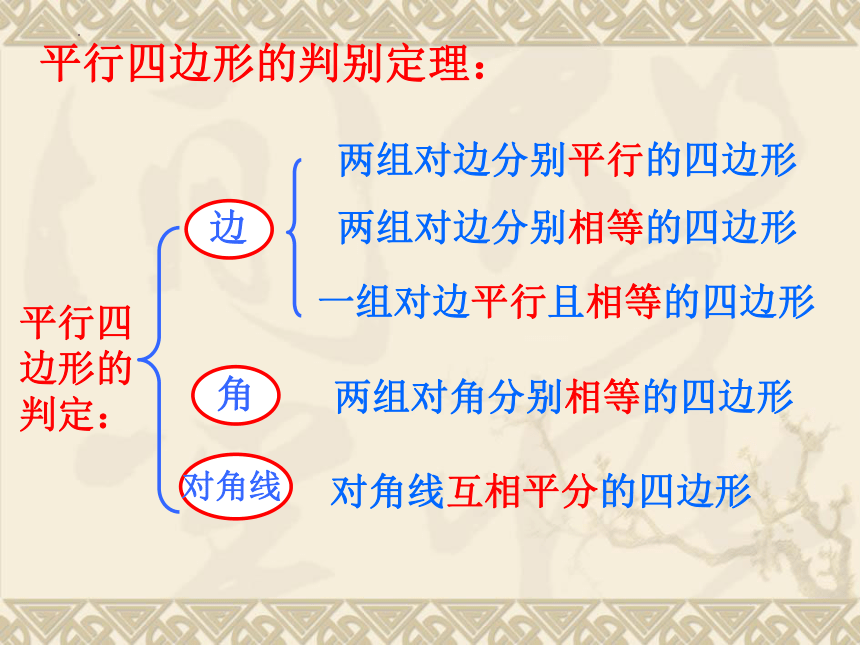
两组对边分别相等的四边形
平行四边形的判定:
边
两组对边分别平行的四边形
角
两组对角分别相等的四边形
对角线
对角线互相平分的四边形
一组对边平行且相等的四边形
平行四边形的判别定理:
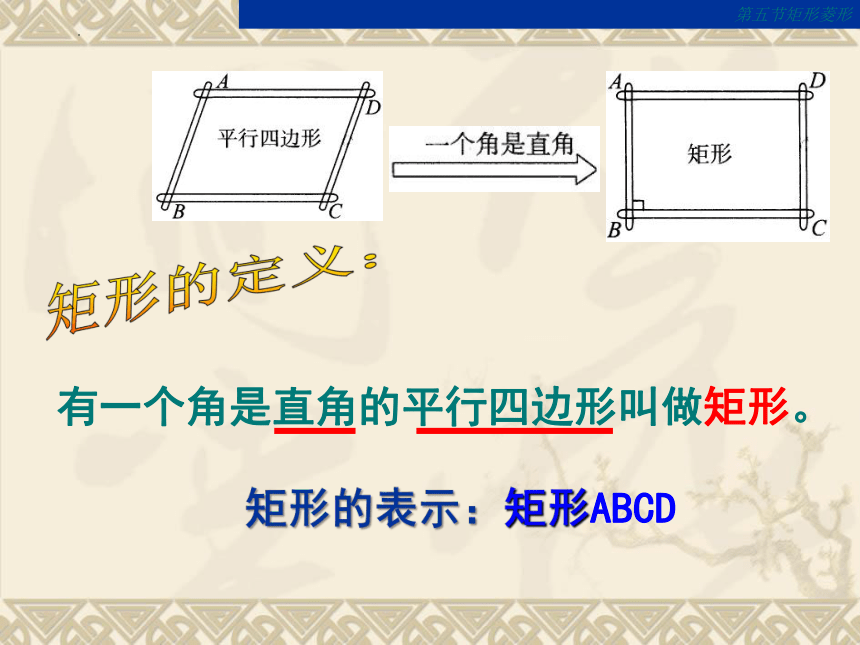
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
情景创设
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,这堂课我们就来研究一种恃殊的平行四边形——
矩形
第五节矩形菱形
有一个角是直角的平行四边形叫做矩形。
矩形的定义:
矩形的表示:矩形ABCD
联系生活
请同学们举出生活中的矩形实例
五星红旗 电视机面 香港区旗 手表
窗框 书桌面 课本封面 地砖
生活中的矩形:
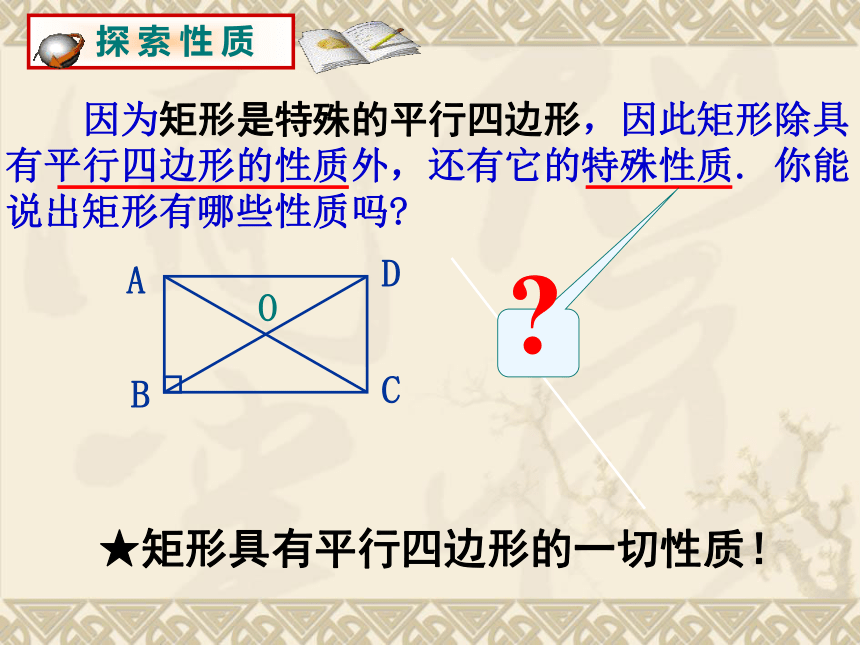
因为矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质. 你能说出矩形有哪些性质吗
O
A
B
C
D
探 索 性 质
★矩形具有平行四边形的一切性质!
探究活动:
矩形是特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
请拉伸活动的平行四边形框架,观察框架在变成矩形的过程中,边、角、对角线各发生了怎样的变化?
请大胆猜想矩形的特殊性质!
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
猜想3:矩形是轴对称图形。
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
★性质定理1:矩形的四个角都是直角
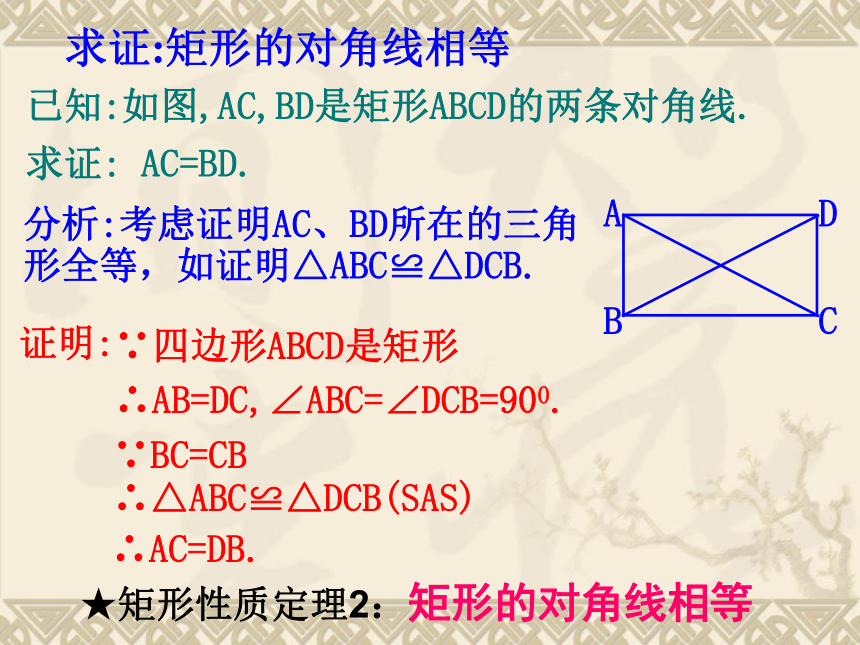
已知:如图,AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
证明:
∵四边形ABCD是矩形
∴AB=DC,∠ABC=∠DCB=900.
分析:考虑证明AC、BD所在的三角形全等,如证明△ABC≌△DCB.
D
B
C
A
∵BC=CB
∴△ABC≌△DCB(SAS)
∴AC=DB.
★矩形性质定理2:矩形的对角线相等
求证:矩形的对角线相等
A
B
C
D
O
矩形的对称性:
★矩形是中心对称图形,又是轴对称图形.
做一做
两条对角线互相平分
对角相等、邻角互补
对边平行且相等
O
A
B
C
D
矩形的性质
对称性
对角线
角
边
矩形
平行四边形
图形
性质
类别
对角线相等且互相平分
四个角都是直角
对边平行且相等
是中心对称图形
中心对称、轴对称图形
A
B
C
D
矩形的性质 边 角 对角线 对称性
对边平行且相等 四个角都是直角 互相平分且相等 中心对称图形
轴对称图形
数学语言 ∵四边形ABCD是矩形 ∴AB∥CD AB=CD AD∥BC AD=BC ∵四边形ABCD是矩形 ∴∠BAD=∠ABC=∠BCD=∠ADC=90° ∵四边形ABCD是矩形 ∴AC=BD ∴OA=OB=OC=OD
A
B
D
C
O
矩形的性质:
议一议:矩形的对角线AC与BD交于点O,那么,BO是Rt△ABC中一条怎样的特殊线段
它与AC有什么大小关系 为什么
D
B
C
A
O
由此可得结论:直角三角形斜边上的中线等于斜边的一半.
BO是Rt△ABC中斜边AC上的中线.
BO等于AC的一半.
∴AC=BD,
继续探索
证明:∵四边形ABCD是矩形
∴
在Rt△ABC中, BO= AC
探究结果:
直角三角形的一个性质:
★直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
A
B
O
C
D
已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
A
B
C
D
∵AD = BD , DE =CD
∴四边形ACBE是平行四边形
E
又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( )
由于CD= CE 所以CD = AB
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
1.矩形的定义:
四边形
两组对边
分别平行
平行四边形
矩形
有一个内角
是直角
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分且相等
对称性:矩形既是轴对称图形又是中心对称图形
边:
角:
对角线:
3.推论:
直角三角形斜边上的中线等于斜边的一半。
板书设计
例1.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
D
C
B
A
O
AD=4cm
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
例2.如图,在矩形ABCD中,DE平分∠ADC交AC于E,交BC于F,若∠BDF=150,求∠DOC、 ∠COF的度数.
A
B
O
C
D
E
F
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
(1)矩形具有而平行四边形不具有的性( )
A. 内角和是360度 B. 对角相等 C. 对边平行且相等 D.对角线相等
(2)下面性质中,矩形不一定具有的( )
A. 对角线相等 B. 四个角相等 C. 是轴对称图形 D. 对角线垂直
课堂练习
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
D
D
四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
试一试
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
3.(2011浙江温州)如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有 ( )
A.2条 B.4条 C.5条 D.6条
A
B
O
C
D
60°
反 馈 练 习
D
试一试
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=90°,
BD是斜边AC上的中线
若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=
6
5
10
120°
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半
(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )
(1).矩形是平行四边形( )
2.矩形的短边长为3cm,两对角线所成的角是60 °,则它的周长 是_______.
3. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.
cm2
4.判断题
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
3. 如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
A
B
C
D
E
F
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半
例.已知:如图, 矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.
分析:
根据矩形的性质,AC=BD,且BD与已知线段AB在RtΔABD中, 故可考虑在ΔABD中求对角线BD之长.
D
B
C
A
O
例 题 欣 赏
由∠AOD=1200,显然应思考ΔABD中锐角的大小,注意∠ADB与∠AOD同在ΔAOD中,容易由矩形对角线的性质求出∠ADB的度数.
例.已知:如图, 矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.
解:
∵四边形ABCD是矩形,
∴BD=2AB=2×2=4(cm).
∴AC=BD,且
∵∠DAB=900
D
B
C
A
O
∵∠AOD=1200
∴∠ODA=∠OAD=
例 题 欣 赏
∴OA=OD.
例.已知:如图, 矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.
解法二:
∵四边形ABCD是矩形,
∴AC=2OA=4(cm).
∴AC=BD,且
∴ΔAOB是等边三角形.
D
B
C
A
O
∵∠AOD=1200,
∴∠AOB=600.
例 题 欣 赏
∴OA=OB.
∴OA=AB=2(cm).
有一个角是直角的
平行四边形叫矩形
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分且相等
1.矩形的定义:
边:
角:
对角线:
5.矩形是轴对称图形,也是中心对称图形.
3.直角三角形斜边上的中线等于斜边的一半
4.矩形的对角线把矩形分成两对全等的
等腰三角形
总结
课 堂 小 结
对角线相等且互相平分
四个角都是直角
对边平行且相等
中心对称、轴对称图形
二、矩形的性质
边:
对角线:
对称性:
角:
三、RtΔ的性质:
直角三角形斜边上的中线等于斜边的一半.
有一个内角是直角的平行四边形叫做矩形.
一、矩形的定义:
练习1:如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.求BD与AD的长.
A
B
O
C
D
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
1.(2011山东潍坊)已知矩形ABCD中,AB=3cm,AD=4cm,过矩形的对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为
_________.
O
A
B
C
D
E
F
能 力 训 练
2.(2011山东泰安)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为 ( )
A. B. C. D.6
A
D
A
B
C
E
O
能 力 训 练
3.已知:如图, △ABC的两条高为BE,CF,点M为BC的中点.
求证:ME=MF.
A
C
B
F
E
M
能 力 训 练
∵∠BEC=900,BM=CM
∵∠BFC=900,BM=CM
∴
∴ME=MF
∴
证明:
4.(2011四川乐山)如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF.
求证:BE=CF.
∴ΔABE≌ΔDCF(SAS)
∴BE=CF
O
A
B
C
D
E
F
能 力 训 练
∠BAE=∠CDF
AB=DC
AE=DF
在ΔABE与ΔDCF中
证明:∵四边形ABCD为矩形
∴AB=DC,AC=DB,
∠ABC=∠DCB=900
∴ΔABC≌ΔDCB(HL)
∴ ∠BAE=∠CDF
4.(2011四川乐山)如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF.
求证:BE=CF.
∴ΔBOE≌ΔCOF(SAS)
∴BE=CF
O
A
B
C
D
E
F
能 力 训 练
∠BOE=∠COF
OB=OC
OE=OF
在ΔBOE与ΔCOF中
证法二:∵四边形ABCD为矩形
∴AC=BD
,
∴OA=OB=OC=OD
又AE=DF,∴OE=OF
(2011山东滨州)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线于点F,连接AE、AF. 那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
解:当点O运动到AC的中点
(或OA=OC)时, 四边形
AECF是矩形.证明如下:
∵CE平分∠BCA
∴∠1=∠2.
∵MN∥BC
∴∠1=∠3.
∴∠2=∠3
∴EO=CO.
同理FO=CO, ∴EO=FO.
又OA=OC
∴四边形AECF是平行四边形.
∵∠1=∠2,∠4=∠5
∴∠1+∠5=∠2+∠4.
∵∠1+∠5+∠2+∠4=180°
∴∠2+∠4=90°即∠ECF=90°
∴四边形AECF是矩形.
F
E
N
M
O
C
B
A
1
2
3
4
5
A
B
C
D
E
F
如图,在矩形ABCD中,E是AB上一点,EF⊥CE交AD于点F,若BE=2,矩形的周长为16,EF=CE,求BC的长.
2
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
如图,△ABC中,∠ACB=900,点D、E分别为AC、AB的中点,点F在BC延长线上,且∠CDF=∠A,
求证:四边形DECF是平行四边形;
A
B
D
C
E
F
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
特殊的平行四边形
18.2.1 矩形
对边平行且相等.
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
平行四边形的特征:
边
角
对角线
温故知新
D
B
A
C
即:AD BC; AB CD
∥
=
∥
=
对角相等、邻角互补.
即:∠A=∠ C ; ∠B=∠D; ∠A+ ∠B= ∠B + ∠ C = ∠C + ∠D =∠D + ∠A =1800
对角线互相平分.
即 AO=CO; BO=DO
对称性:
是中心对称图形,对称中心是对角线的交点.
O
两组对边分别相等的四边形
平行四边形的判定:
边
两组对边分别平行的四边形
角
两组对角分别相等的四边形
对角线
对角线互相平分的四边形
一组对边平行且相等的四边形
平行四边形的判别定理:
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
情景创设
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,这堂课我们就来研究一种恃殊的平行四边形——
矩形
第五节矩形菱形
有一个角是直角的平行四边形叫做矩形。
矩形的定义:
矩形的表示:矩形ABCD
联系生活
请同学们举出生活中的矩形实例
五星红旗 电视机面 香港区旗 手表
窗框 书桌面 课本封面 地砖
生活中的矩形:
因为矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质. 你能说出矩形有哪些性质吗
O
A
B
C
D
探 索 性 质
★矩形具有平行四边形的一切性质!
探究活动:
矩形是特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
请拉伸活动的平行四边形框架,观察框架在变成矩形的过程中,边、角、对角线各发生了怎样的变化?
请大胆猜想矩形的特殊性质!
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
猜想3:矩形是轴对称图形。
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
★性质定理1:矩形的四个角都是直角
已知:如图,AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
证明:
∵四边形ABCD是矩形
∴AB=DC,∠ABC=∠DCB=900.
分析:考虑证明AC、BD所在的三角形全等,如证明△ABC≌△DCB.
D
B
C
A
∵BC=CB
∴△ABC≌△DCB(SAS)
∴AC=DB.
★矩形性质定理2:矩形的对角线相等
求证:矩形的对角线相等
A
B
C
D
O
矩形的对称性:
★矩形是中心对称图形,又是轴对称图形.
做一做
两条对角线互相平分
对角相等、邻角互补
对边平行且相等
O
A
B
C
D
矩形的性质
对称性
对角线
角
边
矩形
平行四边形
图形
性质
类别
对角线相等且互相平分
四个角都是直角
对边平行且相等
是中心对称图形
中心对称、轴对称图形
A
B
C
D
矩形的性质 边 角 对角线 对称性
对边平行且相等 四个角都是直角 互相平分且相等 中心对称图形
轴对称图形
数学语言 ∵四边形ABCD是矩形 ∴AB∥CD AB=CD AD∥BC AD=BC ∵四边形ABCD是矩形 ∴∠BAD=∠ABC=∠BCD=∠ADC=90° ∵四边形ABCD是矩形 ∴AC=BD ∴OA=OB=OC=OD
A
B
D
C
O
矩形的性质:
议一议:矩形的对角线AC与BD交于点O,那么,BO是Rt△ABC中一条怎样的特殊线段
它与AC有什么大小关系 为什么
D
B
C
A
O
由此可得结论:直角三角形斜边上的中线等于斜边的一半.
BO是Rt△ABC中斜边AC上的中线.
BO等于AC的一半.
∴AC=BD,
继续探索
证明:∵四边形ABCD是矩形
∴
在Rt△ABC中, BO= AC
探究结果:
直角三角形的一个性质:
★直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
A
B
O
C
D
已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
A
B
C
D
∵AD = BD , DE =CD
∴四边形ACBE是平行四边形
E
又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( )
由于CD= CE 所以CD = AB
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
1.矩形的定义:
四边形
两组对边
分别平行
平行四边形
矩形
有一个内角
是直角
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分且相等
对称性:矩形既是轴对称图形又是中心对称图形
边:
角:
对角线:
3.推论:
直角三角形斜边上的中线等于斜边的一半。
板书设计
例1.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
D
C
B
A
O
AD=4cm
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
例2.如图,在矩形ABCD中,DE平分∠ADC交AC于E,交BC于F,若∠BDF=150,求∠DOC、 ∠COF的度数.
A
B
O
C
D
E
F
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
(1)矩形具有而平行四边形不具有的性( )
A. 内角和是360度 B. 对角相等 C. 对边平行且相等 D.对角线相等
(2)下面性质中,矩形不一定具有的( )
A. 对角线相等 B. 四个角相等 C. 是轴对称图形 D. 对角线垂直
课堂练习
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
D
D
四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
试一试
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
3.(2011浙江温州)如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有 ( )
A.2条 B.4条 C.5条 D.6条
A
B
O
C
D
60°
反 馈 练 习
D
试一试
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=90°,
BD是斜边AC上的中线
若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=
6
5
10
120°
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半
(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )
(1).矩形是平行四边形( )
2.矩形的短边长为3cm,两对角线所成的角是60 °,则它的周长 是_______.
3. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.
cm2
4.判断题
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
3. 如图四边形ABCD中,∠ABC=∠ADC=900,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
A
B
C
D
E
F
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半
例.已知:如图, 矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.
分析:
根据矩形的性质,AC=BD,且BD与已知线段AB在RtΔABD中, 故可考虑在ΔABD中求对角线BD之长.
D
B
C
A
O
例 题 欣 赏
由∠AOD=1200,显然应思考ΔABD中锐角的大小,注意∠ADB与∠AOD同在ΔAOD中,容易由矩形对角线的性质求出∠ADB的度数.
例.已知:如图, 矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.
解:
∵四边形ABCD是矩形,
∴BD=2AB=2×2=4(cm).
∴AC=BD,且
∵∠DAB=900
D
B
C
A
O
∵∠AOD=1200
∴∠ODA=∠OAD=
例 题 欣 赏
∴OA=OD.
例.已知:如图, 矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=1200,AB=2cm.求矩形对角线的长.
解法二:
∵四边形ABCD是矩形,
∴AC=2OA=4(cm).
∴AC=BD,且
∴ΔAOB是等边三角形.
D
B
C
A
O
∵∠AOD=1200,
∴∠AOB=600.
例 题 欣 赏
∴OA=OB.
∴OA=AB=2(cm).
有一个角是直角的
平行四边形叫矩形
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分且相等
1.矩形的定义:
边:
角:
对角线:
5.矩形是轴对称图形,也是中心对称图形.
3.直角三角形斜边上的中线等于斜边的一半
4.矩形的对角线把矩形分成两对全等的
等腰三角形
总结
课 堂 小 结
对角线相等且互相平分
四个角都是直角
对边平行且相等
中心对称、轴对称图形
二、矩形的性质
边:
对角线:
对称性:
角:
三、RtΔ的性质:
直角三角形斜边上的中线等于斜边的一半.
有一个内角是直角的平行四边形叫做矩形.
一、矩形的定义:
练习1:如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.求BD与AD的长.
A
B
O
C
D
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
1.(2011山东潍坊)已知矩形ABCD中,AB=3cm,AD=4cm,过矩形的对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为
_________.
O
A
B
C
D
E
F
能 力 训 练
2.(2011山东泰安)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为 ( )
A. B. C. D.6
A
D
A
B
C
E
O
能 力 训 练
3.已知:如图, △ABC的两条高为BE,CF,点M为BC的中点.
求证:ME=MF.
A
C
B
F
E
M
能 力 训 练
∵∠BEC=900,BM=CM
∵∠BFC=900,BM=CM
∴
∴ME=MF
∴
证明:
4.(2011四川乐山)如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF.
求证:BE=CF.
∴ΔABE≌ΔDCF(SAS)
∴BE=CF
O
A
B
C
D
E
F
能 力 训 练
∠BAE=∠CDF
AB=DC
AE=DF
在ΔABE与ΔDCF中
证明:∵四边形ABCD为矩形
∴AB=DC,AC=DB,
∠ABC=∠DCB=900
∴ΔABC≌ΔDCB(HL)
∴ ∠BAE=∠CDF
4.(2011四川乐山)如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF.
求证:BE=CF.
∴ΔBOE≌ΔCOF(SAS)
∴BE=CF
O
A
B
C
D
E
F
能 力 训 练
∠BOE=∠COF
OB=OC
OE=OF
在ΔBOE与ΔCOF中
证法二:∵四边形ABCD为矩形
∴AC=BD
,
∴OA=OB=OC=OD
又AE=DF,∴OE=OF
(2011山东滨州)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线于点F,连接AE、AF. 那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
解:当点O运动到AC的中点
(或OA=OC)时, 四边形
AECF是矩形.证明如下:
∵CE平分∠BCA
∴∠1=∠2.
∵MN∥BC
∴∠1=∠3.
∴∠2=∠3
∴EO=CO.
同理FO=CO, ∴EO=FO.
又OA=OC
∴四边形AECF是平行四边形.
∵∠1=∠2,∠4=∠5
∴∠1+∠5=∠2+∠4.
∵∠1+∠5+∠2+∠4=180°
∴∠2+∠4=90°即∠ECF=90°
∴四边形AECF是矩形.
F
E
N
M
O
C
B
A
1
2
3
4
5
A
B
C
D
E
F
如图,在矩形ABCD中,E是AB上一点,EF⊥CE交AD于点F,若BE=2,矩形的周长为16,EF=CE,求BC的长.
2
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
如图,△ABC中,∠ACB=900,点D、E分别为AC、AB的中点,点F在BC延长线上,且∠CDF=∠A,
求证:四边形DECF是平行四边形;
A
B
D
C
E
F
矩形的对边平行且相等 , 矩形的的四个角都是直角
矩形的对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
