2022-2023学年人教版八年级数学下册第十八章 平行四边形 单元检测卷 (含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册第十八章 平行四边形 单元检测卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 238.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形 单元检测卷 2022-2023年度八年级数学下册人教版
一、单选题
1.的比值中,能判断四边形ABCD是平行四边形的是( )
A. B. C. D.
2.如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确的是( )
A.当AB⊥AD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当OA=OB时,四边形ABCD是矩形
D.当AB=AC时,四边形ABCD是菱形
3.如图,对菱形ABCD的叙述正确的是( )
A.AC=BD B.∠OAB=∠OBA
C.AC⊥BD D.有4条对称轴
4.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )cm2
A.4 B.16 C.12 D.8
5.如图,四边形 是平行四边形,点 为 的中点,延长 至点 ,使 ,连接 、 、 ,则在 中 ( )
A. B. C. D.
6.在数学活动课上,老师和同学们判断一个四边形门框是不是矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线,看是否互相平分
B.测量两组对边,看是否分别相等
C.测量对角线,看是否相等
D.测量对角线的交点到四个顶点的距离,看是否都相等
7.下列命题中,正确的是( )
A.有一组邻边相等的四边形是菱形
B.对角线互相平分且垂直的四边形是矩形
C.两组邻角相等的四边形是平行四边形
D.对角线互相垂直且相等的平行四边形是正方形
8.若平行四边形中两个内角的度数比为,则其中较小的内角是( )
A.90° B.60° C.120° D.72°
9.如图,在 中, 是 的中点,作 于点 ,连接 ,下列结论:① ;② ;③ ;④ ;其中正确的个数是( )
A.1 B.2 C.3 D.4
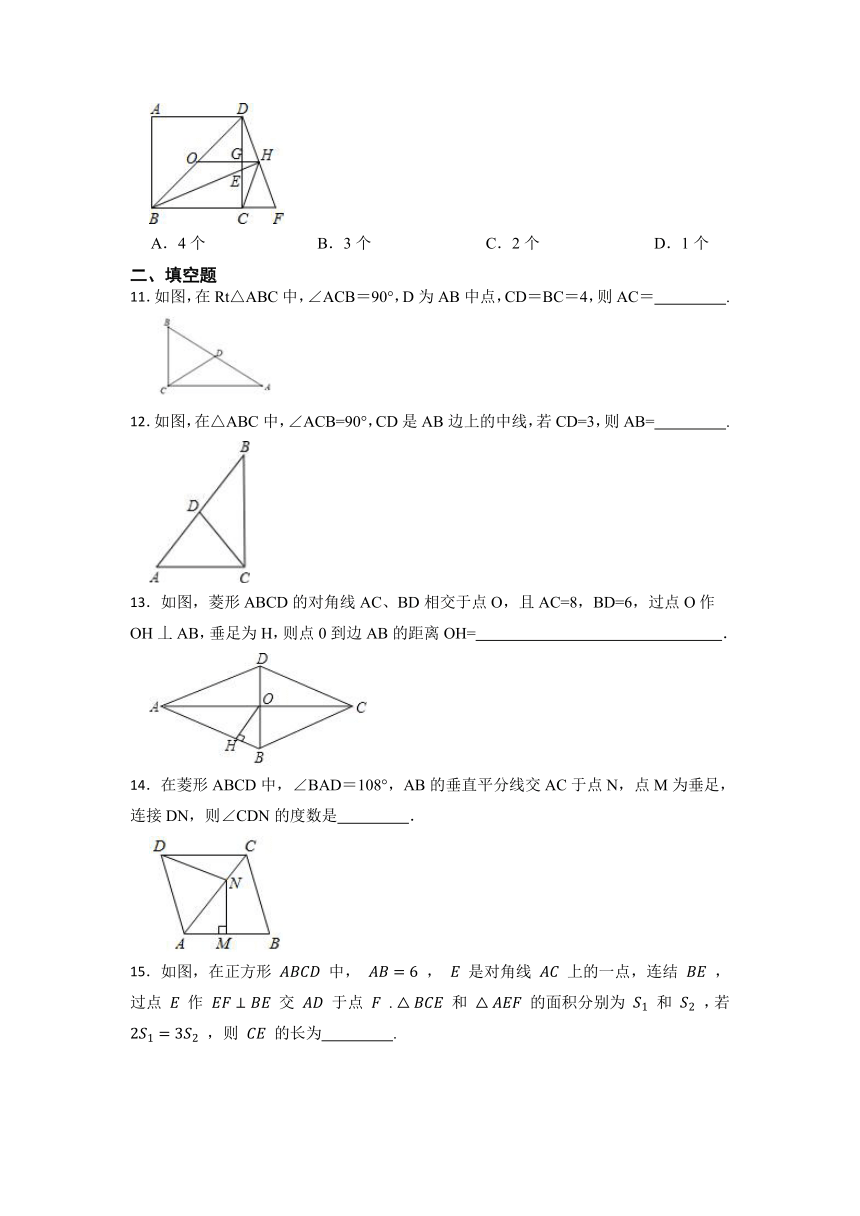
10.如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH= BC,③OD= BF,④∠CHF=45°.正确结论的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,CD=BC=4,则AC= .
12.如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,若CD=3,则AB= .
13.如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH= .
14.在菱形ABCD中,∠BAD=108°,AB的垂直平分线交AC于点N,点M为垂足,连接DN,则∠CDN的度数是 .
15.如图,在正方形 中, , 是对角线 上的一点,连结 ,过点 作 交 于点 . 和 的面积分别为 和 ,若 ,则 的长为 .
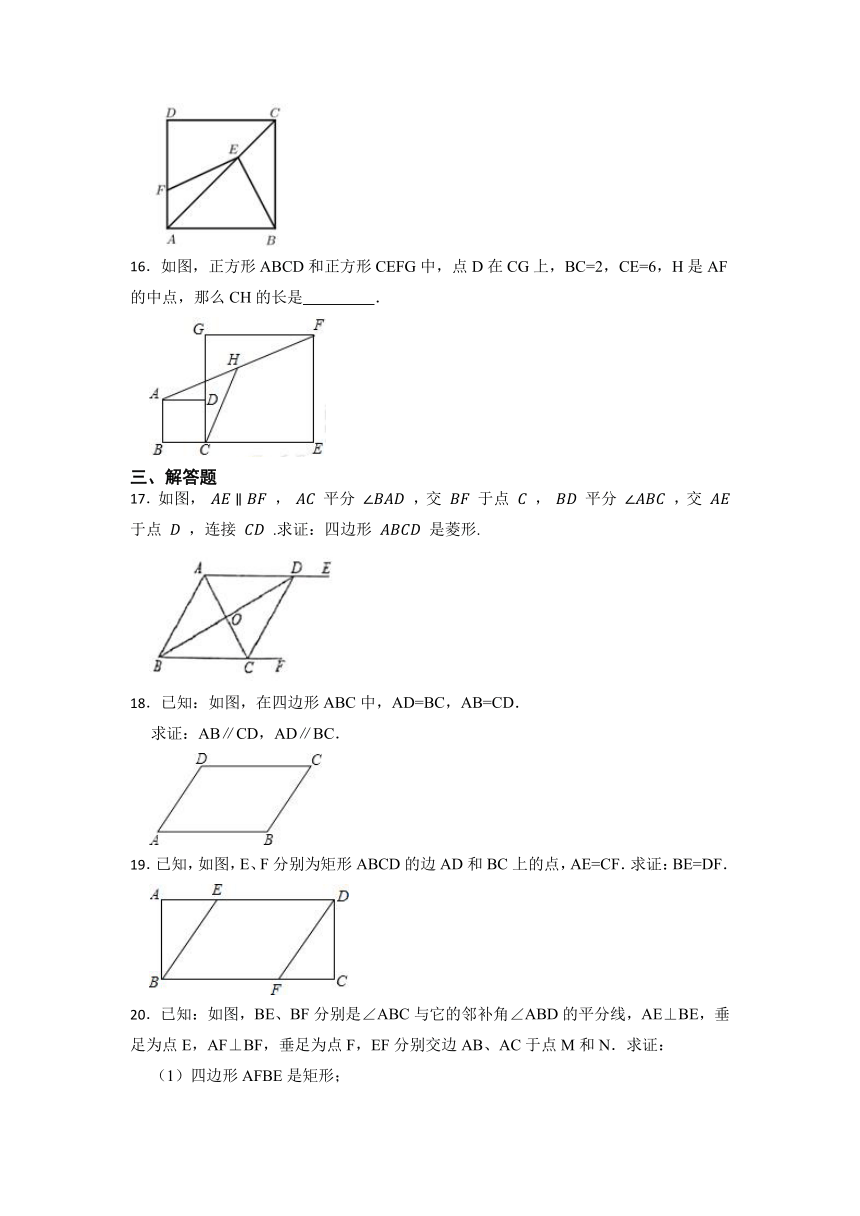
16.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=6,H是AF的中点,那么CH的长是 .
三、解答题
17.如图, , 平分 ,交 于点 , 平分 ,交 于点 ,连接 .求证:四边形 是菱形.
18.已知:如图,在四边形ABC中,AD=BC,AB=CD.
求证:AB∥CD,AD∥BC.
19.已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
20.已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
(1)四边形AFBE是矩形;
(2)MN=BC.
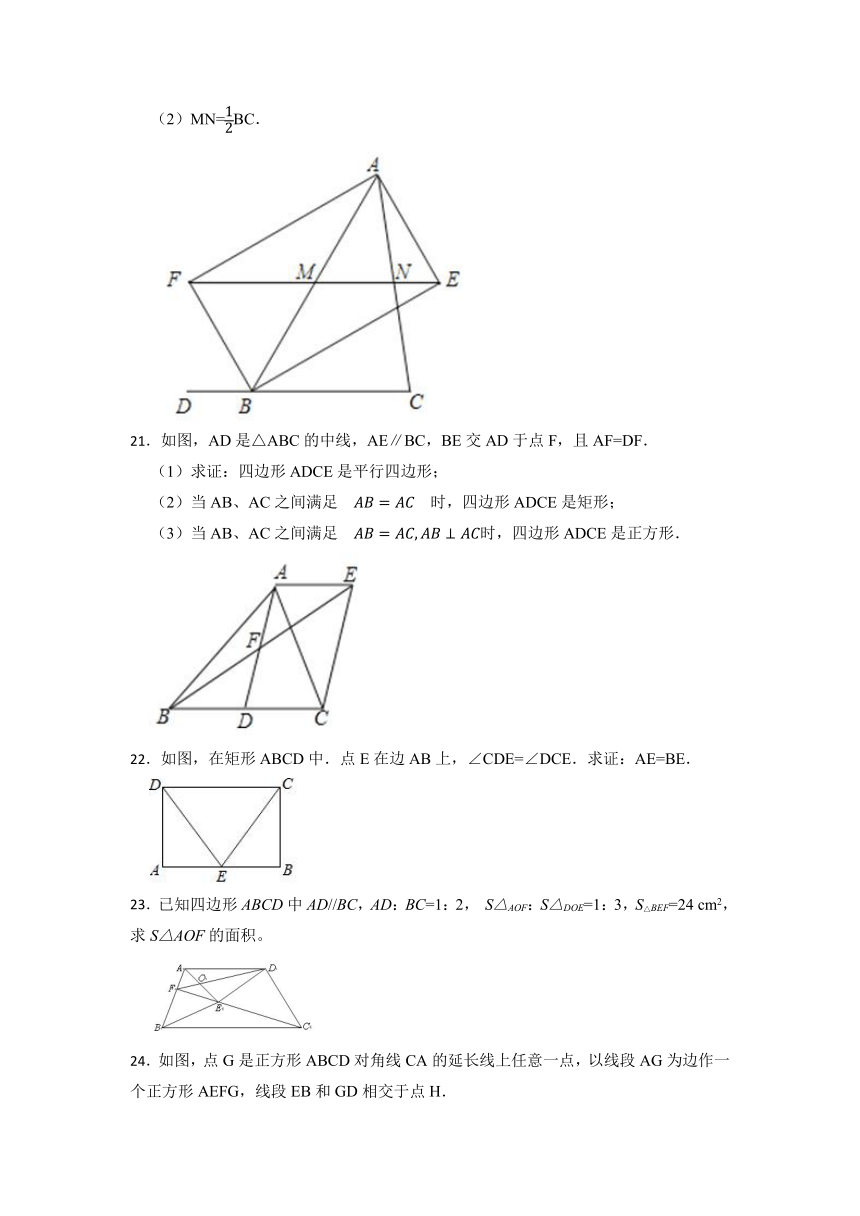
21.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:四边形ADCE是平行四边形;
(2)当AB、AC之间满足 时,四边形ADCE是矩形;
(3)当AB、AC之间满足 时,四边形ADCE是正方形.
22.如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.求证:AE=BE.
23.已知四边形ABCD中AD//BC,AD:BC=1:2, S△AOF:S△DOE=1:3,S△BEF=24 cm2,求S△AOF的面积。
24.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG= ,求EB的长.
答案解析部分
1.【答案】D
【解析】【解答】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D符合条件.
故答案为:D.
【分析】根据两组对角分别相等的四边形是平行四边形进行判断.
2.【答案】D
【解析】【解答】解:A、当AB⊥AD时,∠BAD=90°,根据有一个角是90°的平行四边形是矩形可得四边形ABCD是矩形,故此选项正确,不符合题意;
B、当AC⊥BD时,根据对角线互相垂直的平行四边形是菱形可得四边形ABCD是菱形,故此选项正确,不符合题意;
C、∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
当OA=OB时,可得AO=CO=BO=DO,即AC=BD,
根据对角线相等的平行四边形是矩形可得四边形ABCD是矩形,故此选项正确,不符合题意;
D、当AB=AC时,不能判定平行四边形是矩形,故此选项错误,符合题意.
故答案为:D.
【分析】根据有一个角是直角的平行四边形是矩形可判断A选项;根据对角线互相垂直的平行四边形是菱形,可判断B选项,根据对角线相等的平行四边形是矩形可判断C选项,一条对角线与一边相等的平行四边形不能判断是菱形,据此可判断D选项.
3.【答案】C
【解析】【解答】解:∵菱形的对角线互相垂直
∴AC⊥BC
故答案为:C.
【分析】根据“菱形对角线互相垂直”即可选出答案。
4.【答案】D
【解析】【解答】解:根据正方形的轴对称性可得,阴影部分的面积=S正方形,
∵正方形ABCD的边长为4cm,
∴S阴影=×42=8cm2,
故答案为:D.
【分析】因为正方形是轴对称图形,所以根据正方形的性质得S阴影=S正方形=×边长2可求解.
5.【答案】B
【解析】【解答】连接BF.
设平行四边形AFEO的面积为4m.
∵FO:OC=3:1,BE=OB,AF∥OE
∴S△OBF=S△AOB=m,S△OBC= m,S△AOC= m,
∴S△AOB:S△AOC:S△BOC=m: m: m=3:2:1
故答案为:B.
【分析】连接BF,设平行四边形AFEO的面积为4m.根据等底同高的三角形的面积相等得出S△OBF=S△AOB=m,同高三角形的面积之比等于底之比得出S△OBC= m,S△AOC= m,从而得出答案。
6.【答案】D
【解析】【解答】解:A、对角线相互平分可以判定平行四边形,A选项不符合题意;
B、两组对边相等可以判定平行四边形,B选项不符合题意;
C、对角线相等的四边形不一定为矩形,C选项不符合题意;
D、对角线相等且平分的四边形为矩形,可知对角线的交点到四个顶点距离是否相等,可判断四边形是否为矩形,D选项符合题意.
故答案为:D.
【分析】根据矩形的判定定理:有一个角是直角的平行四边形为矩形;有三个角是直角的四边形为矩形;对角线相等且平分的四边形为矩形,据此判断即可.
7.【答案】D
【解析】【解答】解:A、有一组邻边相等的平行四边形是菱形,故本选项错误;
B、对角线互相平分且垂直的四边形是菱形,故本选项错误;
C、两组对角相等的四边形是平行四边形,故本选项错误;
D、对角线互相垂直且相等的平行四边形是正方形,故本选项正确.
故选D.
【分析】分别根据菱形、矩形、正方形及平行四边形的判定定理对各选项进行逐一分析即可.
8.【答案】D
【解析】【解答】解:∵四边形ABCD是平行四边形
∴ABCD,
∴∠B+∠C=180°,
∵∠B:∠C=2:3,
∴∠B=×180°=72°,
故答案为:D.
【分析】根据平行四边形的性质可得∠B+∠C=180°,再结合∠B:∠C=2:3,求出∠B=×180°=72°即可。
9.【答案】C
【解析】【解答】∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AD//BC,
∵AB=2AD,CD=2CF,
∴CF=CB,
∴∠CBF=∠CFB,
∵CD∥AB,
∴∠CFB=∠ABF,
∴ ,故①符合题意;
延长EF交BC的延长线与M,
∵AD//BC,
∴∠DEF=∠M,
又∵∠DFE=∠CFM,DF=CF,
∴△DFE与△CFM(AAS),
∴EF=FM= EM,
∵BF⊥AD,
∴∠AEB=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠CBE=∠AEB=90°,
∴BF= EM,
∴BF=EF,故②符合题意;
∵EF=FM,
∴S△BEF=S△BMF,
∵△DFE≌△CFM,
∴S△DFE=S△CFM,
∴S△EBF=S△BMF=S△EDF+S△FBC,
∴ ,故③符合题意;
过点F作FN⊥BE,垂足为N,则∠FNE=90°,
∴∠AEB=∠FEN,
∴AD//EF,
∴∠DEF=∠EFN,
又∵EF=FB,
∴∠BFE=2∠EFN,
∴∠BFE=2∠DEF,故④不符合题意,
所以正确的有3个,
故答案为:C.
【分析】由平行四边形的性质结合AB=2AD,CD=2CF可得CF=CB,从而可得∠CBF=∠CFB,再根据CD∥AB,得∠CFB=∠ABF,继而可得 ,可以判断①符合题意;延长EF交BC的延长线与M,证明△DFE与△CFM(AAS),继而得EF=FM= EM,证明∠CBE=∠AEB=90°,然后根据直角三角形斜边中线的性质即可判断②符合题意;由上可得S△BEF=S△BMF,S△DFE=S△CFM,继而可得S△EBF=S△BMF=S△EDF+S△FBC,继而可得 ,可判断③符合题意;过点F作FN⊥BE,垂足为N,则∠FNE=90°,则可得AD//FN,则有∠DEF=∠EFN,根据等腰三角形的性质可得∠BFE=2∠EFN,继而得∠BFE=2∠DEF,判断④不符合题意.
10.【答案】C
【解析】【解答】解:∵EC=CF,∠BCE=∠DCF,BC=DC,
∴△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠CBE+∠BEC=90°,∠BEC=∠DEH,
∴∠DEH+∠CDF=90°,
∴∠BHD=∠BHF=90°,
∵BH=BH,∠HBD=∠HBF,
∴△BHD≌△BHF,
∴DH=HF,∵OD=OB
∴OH是△DBF的中位线
∴OH∥BF;故①正确;
∴OH= BF,∠DOH=∠CBD=45°,
∵OH是△BFD的中位线,
∴DG=CG= BC,GH= CF,
∵CE=CF,
∴GH= CF= CE
∵CE<CG= BC,
∴GH< BC,故②错误.
∵四边形ABCD是正方形,BE是∠DBC的平分线,
∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,
∵CE=CF,
∴Rt△BCE≌Rt△DCF,
∴∠EBC=∠CDF=22.5°,
∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,
∵OH是△DBF的中位线,CD⊥AF,
∴OH是CD的垂直平分线,
∴DH=CH,
∴∠CDF=∠DCH=22.5°,
∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,
∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故④正确;
∴∠ODH=∠BDC+∠CDF=67.5°,
∴∠OHD=180°﹣∠ODH﹣∠DOH=67.5°,
∴∠ODH=∠OHD,
∴OD=OH= BF;故③正确.
故答案为:C.
【分析】 ① 作EJ⊥BD于J,连接EF,由SAS判定△BCE≌△DCF,再由平行线的性质得出OH是△DBF的中位线即可求解;
② 根据OH是△DBF的中位线,得出GH= CF,由GH< BC,可得出结论;
③ 易证得△ODH是等腰三角形,进而证得OD= BF;
④ 根据四边形ABCD是正方形,BE是∠DBC的平分线可求出Rt△BCE≌Rt△DCF,再由∠EBC=22.5°即可求出结论.
11.【答案】
【解析】【解答】∵∠ACB=90°,D为AB中点
∴CD=BD=AD=4
∴AB=2CD=8
根据勾股定理可知
故答案为 .
【分析】根据直角三角形斜边中点性质和勾股定理即可解答.
12.【答案】6
【解析】【解答】∵在Rt△ABC中,∠ACB=90°,CD=3,CD是AB边上的中线,
∴AB=2CD=6.
【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AB,则AB=2CD可求解。
13.【答案】
【解析】【解答】解:∵AC=8,BD=6,
∴BO=3,AO=4,
∴AB=5.
AO BO= AB OH,
OH= .
故答案为: .
【分析】因为菱形的对角线互相垂直平分,菱形的四边相等,根据面积相等,可求出OH的长.
14.【答案】18°
【解析】【解答】解:如图,连接BN,
∵在菱形ABCD中,∠BAD=108°,
∴AD=AB,∠ABC=72°,∠CAB=54°,
∵AB的垂直平分线交AC于点N,
∴AN=NB,
∴∠CAB=∠ABN=54°,
∴∠CBN=72°-54°=18°,
在△DCN和△BCN中,
,
∴△DCN≌△BCN(SAS),
∴∠CDN=∠CBN=18°,
故答案为:18°.
【分析】根据菱形的性质可得AD=AB,∠ABC=72°,∠CAB=54°,再根据三角形的判定方法SAS,证明△DCN≌△BCN,最后求解即可。
15.【答案】
【解析】【解答】解:连接ED,过E作MN⊥BC于N,交AD于M,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=6,∠ABC=∠BCD=∠ADC=∠DAB=90°,
∴∠1=∠2=45°,
∵MN⊥BC,
∴∠ENC=∠ENB=90°,
∴四边形MNCD是矩形,
∴MN=CD=6,DM=CN,∠DME=90°,
在△CDE和△CBE中,
,
∴△CDE≌△CBE(SAS),
∴ED=EB,∠EDC=∠EBC,
∵∠CDA=∠CBA=90°,
∴∠CDA-∠EDC=∠CBA-∠EBC,
即∠ADE=∠ABE,
∵EF⊥BE,
∴∠FEB=90°,
∵∠FEB+∠DAB+∠AFE+∠ABE=360°,
∴∠AFE+∠ABE=360°-∠FEB-∠DAB=180°,
∵∠AFE+∠EFD=180°,
∴∠ABE=∠EFD,
∴∠ADE=∠EFD,
∴ED=EF,
∵∠DME=90°,
∴EM⊥DF,
∴DM=MF,
在△NEC中,∠1=45°,
∴△NEC是等腰直角三角形,
设NE=NC=x,
则CE= x,DM=MF=CN=x,
∴AF=AD-DM-MF=6-2x,
ME=MN-EN=6-x,
∴ , ,
∵ ,
∴ ,
解得: , (舍),
∴CE= ,
故答案为: .
【分析】连接ED,过E作MN⊥BC于N,交AD于M,由正方形的性质可推出∠1=∠2=45°,推出四边形MNCD是矩形,然后证明△CDE≌△CBE,由全等三角形的性质以及角的和差关系可得∠ADE=∠ABE,根据四边形内角和为360°可得∠AFE+∠ABE=180°,进而得到∠ADE=∠EFD,则ED=EF,结合等腰三角形的性质可得DM=MF,由∠1=45°可得△NEC是等腰直角三角形,设NE=NC=x,则CE=x,DM=MF=CN=x,AF=6-2x,ME=6-x,然后表示出S1、S2,结合2S1=3S2就可求得x的值,进而得到CE的值.
16.【答案】2
【解析】【解答】解:如图,连接AC、CF,
在正方形ABCD和正方形CEFG中,AC= BC=2 ,CF= CE=6 ,
∠ACD=∠GCF=45°,
所以,∠ACF=45°+45°=90°,
所以,△ACF是直角三角形,
由勾股定理得,AF=
=
=4 ,
∵H是AF的中点,
∴CH= AF= ×4 =2 .
故答案为2 .
【分析】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,难点在于作辅助线构造出直角三角形.连接AC、CF,根据正方形的性质求出AC、CF,并判断出△ACF是直角三角形,再利用勾股定理列式求出AF,然后根据直角三角形斜边上的中线等于斜边的一半解答.
17.【答案】证明:∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
同理 .
∴ ,
∵ ,
∴ 且 ,
∴四边形 是平行四边形,
∵ ,
∴四边形 是菱形.
【解析】【分析】由角平分线和平行线的性质先证出 , ,从而有 ,得到四边形 是平行四边形,又因为 ,所以四边形 是菱形.
18.【答案】证明:连接AC,
在△ADB和△CBD中,
∵ ,
∴△ADB≌△CBD(SSS),
∴∠DCA=∠CAB,∠DAC=∠ACB,
∴AB∥CD,AD∥BC.
【解析】【分析】连接AC,利用三边对应相等的两个三角形全等,证明△ADB≌△CBD,再利用全等的性质可得∠DCA=∠CAB,∠DAC=∠ACB,进而证明AB∥CD,AD∥BC.
19.【答案】证明:证法一:∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=90°.
在△ABE和△CDF中
∵ , ∴△ABE≌△CDF(SAS),
∴BE=DF(全等三角形对应边相等)
证法二:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵AE=CF,∴AD-AE=BC-CF
即ED=BF,
而ED∥BF,
∴四边形BFDE为平行四边形
∴BE=DF(平行四边形对边相等).
利用全等三角形对应边相等求证
【解析】【分析】证法一利用三角形全等来证明对应边相等;证法二利用矩形的性质及AE=CF证得四边形BFDE为平行四边形,进而利用平行四边形对边相等证得BE=DF.
20.【答案】证明:(1)∵BE、BF分别是△ABC中∠B及它的外角的平分线,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵AE⊥BE,E为垂足,AF⊥BF,F为垂足,
∴∠AFB=∠AEB=90°,
∴四边形AEBF为矩形;
(2)∵四边形AEBF为矩形,
∴BM=MA=ME,
∴∠2=∠5,
∵∠2=∠1,
∴∠1=∠5,
∴ME∥BC,
∵M是AB的中点,
∴N为AC的中点,
∴MN=BC.
【解析】【分析】(1)由BE、BE是角平分线可得∠EBF是90°,进而由条件中的两个垂直可得两个直角,可得四边形AEBF是矩形;
(2)由矩形的F质可得∠2=∠5进而利用角平分线的性质可得∠1=∠5,可得ME∥BC,进而可得N为AC中点,根据三角形中位线性质求出即可.
21.【答案】(1)证明:∵AD是△ABC的中线,∴BD=CD,∵AE∥BC,∴∠AEF=∠DBF,在△AFE和△DFB中,,∴△AFE≌△DFB(AAS),∴AE=BD,∴AE=CD,∵AE∥BC,∴四边形ADCE是平行四边形;(2)当AB=AC时,四边形ADCE是矩形;∵AB=AC,AD是△ABC的中线,∴AD⊥BC,∴∠ADC=90°,∵四边形ADCE是平行四边形,∴四边形ADCE是矩形,故答案为:AB=AC;(3)当AB⊥AC,AB=AC时,四边形ADCE是正方形,∵AB⊥AC,AB=AC,∴△ABC是等腰直角三角形,∵AD是△ABC的中线,∴AD=CD,AD⊥BC,又∵四边形ADCE是平行四边形,∴四边形ADCE是正方形,故答案为:AB⊥AC,AB=AC.
【解析】【分析】(1)首先证明△AFE≌△DFB可得AE=BD,进而可证明AE=CD,再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;
(2)当AB=AC时,根据等腰三角形三线合一可得AD⊥BC,再根据有一个角是直角的平行四边形是矩形可得结论;
(3)当AB=AC,AB⊥AC时,△ABC是等腰直角三角形,根据直角三角形斜边上的中线等于斜边的一半可得AD=CD,根据等腰三角形的性质可得AD⊥BC,从而可得证明四边形ADCE是正方形.
22.【答案】证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵∠CDE=∠DCE,
∴DE=CE,
在Rt△DAE和Rt△CBE中, ,
∴Rt△DAE≌Rt△CBE(HL),
∴AE=BE
【解析】【分析】证出DE=CE,由HL证明Rt△DAE≌Rt△CBE,得出对应边相等即可.
23.【答案】6
【解析】【解答】解 :如图,取BC的中点G,连接DG、EG、FG.
∵ AD∶BC=1∶2 ;G是BC的中点,
∴ BG=AD ;
又∵AD//BC ;
∴四边形ABGD是平行四边形;
∴S△ADE+S△BEG=S平行四边形ABDG
S△AFD+S△BG=S平行四边形ABDG
∴上面两个三角形的面积差与下面两个三角形面积差相等。
∵上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍。
下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12
∴S△AOF=12÷2=6m2.
【分析】如图,取BC的中点G,连接DG、EG、FG.根据一组对边平行且相等的四边形是平行四边形得出四边形ABGD是平行四边形; 根据平行四边形的面积公式,三角形的面积计算公式得出S△ADE+S△BEG=S平行四边形ABDG,S△AFD+S△BG=S平行四边形ABDG;从而得出上面两个三角形的面积差与下面两个三角形面积差相等;进而得出上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍;下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12;从而得出答案。
24.【答案】(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,
∴BD⊥CG,
∵AB=AD=2,在Rt△ABD中,DB= ,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA= ,
即OG=OA+AG= + =2 ,
∴EB=GD= .
【解析】【分析】(1)在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,得到∠GAD=∠EAB从而△GAD≌△EAB,即EB=GD;(2)EB⊥GD,由(1)得∠ADG=∠ABE则在△BDH中,∠DHB=90°所以EB⊥GD;(3)设BD与AC交于点O,由AB=AD=2在Rt△ABD中求得DB,所以得到结果.
一、单选题
1.的比值中,能判断四边形ABCD是平行四边形的是( )
A. B. C. D.
2.如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确的是( )
A.当AB⊥AD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当OA=OB时,四边形ABCD是矩形
D.当AB=AC时,四边形ABCD是菱形
3.如图,对菱形ABCD的叙述正确的是( )
A.AC=BD B.∠OAB=∠OBA
C.AC⊥BD D.有4条对称轴
4.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )cm2
A.4 B.16 C.12 D.8
5.如图,四边形 是平行四边形,点 为 的中点,延长 至点 ,使 ,连接 、 、 ,则在 中 ( )
A. B. C. D.
6.在数学活动课上,老师和同学们判断一个四边形门框是不是矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线,看是否互相平分
B.测量两组对边,看是否分别相等
C.测量对角线,看是否相等
D.测量对角线的交点到四个顶点的距离,看是否都相等
7.下列命题中,正确的是( )
A.有一组邻边相等的四边形是菱形
B.对角线互相平分且垂直的四边形是矩形
C.两组邻角相等的四边形是平行四边形
D.对角线互相垂直且相等的平行四边形是正方形
8.若平行四边形中两个内角的度数比为,则其中较小的内角是( )
A.90° B.60° C.120° D.72°
9.如图,在 中, 是 的中点,作 于点 ,连接 ,下列结论:① ;② ;③ ;④ ;其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH= BC,③OD= BF,④∠CHF=45°.正确结论的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,CD=BC=4,则AC= .
12.如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,若CD=3,则AB= .
13.如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH= .
14.在菱形ABCD中,∠BAD=108°,AB的垂直平分线交AC于点N,点M为垂足,连接DN,则∠CDN的度数是 .
15.如图,在正方形 中, , 是对角线 上的一点,连结 ,过点 作 交 于点 . 和 的面积分别为 和 ,若 ,则 的长为 .
16.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=6,H是AF的中点,那么CH的长是 .
三、解答题
17.如图, , 平分 ,交 于点 , 平分 ,交 于点 ,连接 .求证:四边形 是菱形.
18.已知:如图,在四边形ABC中,AD=BC,AB=CD.
求证:AB∥CD,AD∥BC.
19.已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
20.已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
(1)四边形AFBE是矩形;
(2)MN=BC.
21.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:四边形ADCE是平行四边形;
(2)当AB、AC之间满足 时,四边形ADCE是矩形;
(3)当AB、AC之间满足 时,四边形ADCE是正方形.
22.如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.求证:AE=BE.
23.已知四边形ABCD中AD//BC,AD:BC=1:2, S△AOF:S△DOE=1:3,S△BEF=24 cm2,求S△AOF的面积。
24.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG= ,求EB的长.
答案解析部分
1.【答案】D
【解析】【解答】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D符合条件.
故答案为:D.
【分析】根据两组对角分别相等的四边形是平行四边形进行判断.
2.【答案】D
【解析】【解答】解:A、当AB⊥AD时,∠BAD=90°,根据有一个角是90°的平行四边形是矩形可得四边形ABCD是矩形,故此选项正确,不符合题意;
B、当AC⊥BD时,根据对角线互相垂直的平行四边形是菱形可得四边形ABCD是菱形,故此选项正确,不符合题意;
C、∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
当OA=OB时,可得AO=CO=BO=DO,即AC=BD,
根据对角线相等的平行四边形是矩形可得四边形ABCD是矩形,故此选项正确,不符合题意;
D、当AB=AC时,不能判定平行四边形是矩形,故此选项错误,符合题意.
故答案为:D.
【分析】根据有一个角是直角的平行四边形是矩形可判断A选项;根据对角线互相垂直的平行四边形是菱形,可判断B选项,根据对角线相等的平行四边形是矩形可判断C选项,一条对角线与一边相等的平行四边形不能判断是菱形,据此可判断D选项.
3.【答案】C
【解析】【解答】解:∵菱形的对角线互相垂直
∴AC⊥BC
故答案为:C.
【分析】根据“菱形对角线互相垂直”即可选出答案。
4.【答案】D
【解析】【解答】解:根据正方形的轴对称性可得,阴影部分的面积=S正方形,
∵正方形ABCD的边长为4cm,
∴S阴影=×42=8cm2,
故答案为:D.
【分析】因为正方形是轴对称图形,所以根据正方形的性质得S阴影=S正方形=×边长2可求解.
5.【答案】B
【解析】【解答】连接BF.
设平行四边形AFEO的面积为4m.
∵FO:OC=3:1,BE=OB,AF∥OE
∴S△OBF=S△AOB=m,S△OBC= m,S△AOC= m,
∴S△AOB:S△AOC:S△BOC=m: m: m=3:2:1
故答案为:B.
【分析】连接BF,设平行四边形AFEO的面积为4m.根据等底同高的三角形的面积相等得出S△OBF=S△AOB=m,同高三角形的面积之比等于底之比得出S△OBC= m,S△AOC= m,从而得出答案。
6.【答案】D
【解析】【解答】解:A、对角线相互平分可以判定平行四边形,A选项不符合题意;
B、两组对边相等可以判定平行四边形,B选项不符合题意;
C、对角线相等的四边形不一定为矩形,C选项不符合题意;
D、对角线相等且平分的四边形为矩形,可知对角线的交点到四个顶点距离是否相等,可判断四边形是否为矩形,D选项符合题意.
故答案为:D.
【分析】根据矩形的判定定理:有一个角是直角的平行四边形为矩形;有三个角是直角的四边形为矩形;对角线相等且平分的四边形为矩形,据此判断即可.
7.【答案】D
【解析】【解答】解:A、有一组邻边相等的平行四边形是菱形,故本选项错误;
B、对角线互相平分且垂直的四边形是菱形,故本选项错误;
C、两组对角相等的四边形是平行四边形,故本选项错误;
D、对角线互相垂直且相等的平行四边形是正方形,故本选项正确.
故选D.
【分析】分别根据菱形、矩形、正方形及平行四边形的判定定理对各选项进行逐一分析即可.
8.【答案】D
【解析】【解答】解:∵四边形ABCD是平行四边形
∴ABCD,
∴∠B+∠C=180°,
∵∠B:∠C=2:3,
∴∠B=×180°=72°,
故答案为:D.
【分析】根据平行四边形的性质可得∠B+∠C=180°,再结合∠B:∠C=2:3,求出∠B=×180°=72°即可。
9.【答案】C
【解析】【解答】∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AD//BC,
∵AB=2AD,CD=2CF,
∴CF=CB,
∴∠CBF=∠CFB,
∵CD∥AB,
∴∠CFB=∠ABF,
∴ ,故①符合题意;
延长EF交BC的延长线与M,
∵AD//BC,
∴∠DEF=∠M,
又∵∠DFE=∠CFM,DF=CF,
∴△DFE与△CFM(AAS),
∴EF=FM= EM,
∵BF⊥AD,
∴∠AEB=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠CBE=∠AEB=90°,
∴BF= EM,
∴BF=EF,故②符合题意;
∵EF=FM,
∴S△BEF=S△BMF,
∵△DFE≌△CFM,
∴S△DFE=S△CFM,
∴S△EBF=S△BMF=S△EDF+S△FBC,
∴ ,故③符合题意;
过点F作FN⊥BE,垂足为N,则∠FNE=90°,
∴∠AEB=∠FEN,
∴AD//EF,
∴∠DEF=∠EFN,
又∵EF=FB,
∴∠BFE=2∠EFN,
∴∠BFE=2∠DEF,故④不符合题意,
所以正确的有3个,
故答案为:C.
【分析】由平行四边形的性质结合AB=2AD,CD=2CF可得CF=CB,从而可得∠CBF=∠CFB,再根据CD∥AB,得∠CFB=∠ABF,继而可得 ,可以判断①符合题意;延长EF交BC的延长线与M,证明△DFE与△CFM(AAS),继而得EF=FM= EM,证明∠CBE=∠AEB=90°,然后根据直角三角形斜边中线的性质即可判断②符合题意;由上可得S△BEF=S△BMF,S△DFE=S△CFM,继而可得S△EBF=S△BMF=S△EDF+S△FBC,继而可得 ,可判断③符合题意;过点F作FN⊥BE,垂足为N,则∠FNE=90°,则可得AD//FN,则有∠DEF=∠EFN,根据等腰三角形的性质可得∠BFE=2∠EFN,继而得∠BFE=2∠DEF,判断④不符合题意.
10.【答案】C
【解析】【解答】解:∵EC=CF,∠BCE=∠DCF,BC=DC,
∴△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠CBE+∠BEC=90°,∠BEC=∠DEH,
∴∠DEH+∠CDF=90°,
∴∠BHD=∠BHF=90°,
∵BH=BH,∠HBD=∠HBF,
∴△BHD≌△BHF,
∴DH=HF,∵OD=OB
∴OH是△DBF的中位线
∴OH∥BF;故①正确;
∴OH= BF,∠DOH=∠CBD=45°,
∵OH是△BFD的中位线,
∴DG=CG= BC,GH= CF,
∵CE=CF,
∴GH= CF= CE
∵CE<CG= BC,
∴GH< BC,故②错误.
∵四边形ABCD是正方形,BE是∠DBC的平分线,
∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,
∵CE=CF,
∴Rt△BCE≌Rt△DCF,
∴∠EBC=∠CDF=22.5°,
∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,
∵OH是△DBF的中位线,CD⊥AF,
∴OH是CD的垂直平分线,
∴DH=CH,
∴∠CDF=∠DCH=22.5°,
∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,
∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故④正确;
∴∠ODH=∠BDC+∠CDF=67.5°,
∴∠OHD=180°﹣∠ODH﹣∠DOH=67.5°,
∴∠ODH=∠OHD,
∴OD=OH= BF;故③正确.
故答案为:C.
【分析】 ① 作EJ⊥BD于J,连接EF,由SAS判定△BCE≌△DCF,再由平行线的性质得出OH是△DBF的中位线即可求解;
② 根据OH是△DBF的中位线,得出GH= CF,由GH< BC,可得出结论;
③ 易证得△ODH是等腰三角形,进而证得OD= BF;
④ 根据四边形ABCD是正方形,BE是∠DBC的平分线可求出Rt△BCE≌Rt△DCF,再由∠EBC=22.5°即可求出结论.
11.【答案】
【解析】【解答】∵∠ACB=90°,D为AB中点
∴CD=BD=AD=4
∴AB=2CD=8
根据勾股定理可知
故答案为 .
【分析】根据直角三角形斜边中点性质和勾股定理即可解答.
12.【答案】6
【解析】【解答】∵在Rt△ABC中,∠ACB=90°,CD=3,CD是AB边上的中线,
∴AB=2CD=6.
【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AB,则AB=2CD可求解。
13.【答案】
【解析】【解答】解:∵AC=8,BD=6,
∴BO=3,AO=4,
∴AB=5.
AO BO= AB OH,
OH= .
故答案为: .
【分析】因为菱形的对角线互相垂直平分,菱形的四边相等,根据面积相等,可求出OH的长.
14.【答案】18°
【解析】【解答】解:如图,连接BN,
∵在菱形ABCD中,∠BAD=108°,
∴AD=AB,∠ABC=72°,∠CAB=54°,
∵AB的垂直平分线交AC于点N,
∴AN=NB,
∴∠CAB=∠ABN=54°,
∴∠CBN=72°-54°=18°,
在△DCN和△BCN中,
,
∴△DCN≌△BCN(SAS),
∴∠CDN=∠CBN=18°,
故答案为:18°.
【分析】根据菱形的性质可得AD=AB,∠ABC=72°,∠CAB=54°,再根据三角形的判定方法SAS,证明△DCN≌△BCN,最后求解即可。
15.【答案】
【解析】【解答】解:连接ED,过E作MN⊥BC于N,交AD于M,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=6,∠ABC=∠BCD=∠ADC=∠DAB=90°,
∴∠1=∠2=45°,
∵MN⊥BC,
∴∠ENC=∠ENB=90°,
∴四边形MNCD是矩形,
∴MN=CD=6,DM=CN,∠DME=90°,
在△CDE和△CBE中,
,
∴△CDE≌△CBE(SAS),
∴ED=EB,∠EDC=∠EBC,
∵∠CDA=∠CBA=90°,
∴∠CDA-∠EDC=∠CBA-∠EBC,
即∠ADE=∠ABE,
∵EF⊥BE,
∴∠FEB=90°,
∵∠FEB+∠DAB+∠AFE+∠ABE=360°,
∴∠AFE+∠ABE=360°-∠FEB-∠DAB=180°,
∵∠AFE+∠EFD=180°,
∴∠ABE=∠EFD,
∴∠ADE=∠EFD,
∴ED=EF,
∵∠DME=90°,
∴EM⊥DF,
∴DM=MF,
在△NEC中,∠1=45°,
∴△NEC是等腰直角三角形,
设NE=NC=x,
则CE= x,DM=MF=CN=x,
∴AF=AD-DM-MF=6-2x,
ME=MN-EN=6-x,
∴ , ,
∵ ,
∴ ,
解得: , (舍),
∴CE= ,
故答案为: .
【分析】连接ED,过E作MN⊥BC于N,交AD于M,由正方形的性质可推出∠1=∠2=45°,推出四边形MNCD是矩形,然后证明△CDE≌△CBE,由全等三角形的性质以及角的和差关系可得∠ADE=∠ABE,根据四边形内角和为360°可得∠AFE+∠ABE=180°,进而得到∠ADE=∠EFD,则ED=EF,结合等腰三角形的性质可得DM=MF,由∠1=45°可得△NEC是等腰直角三角形,设NE=NC=x,则CE=x,DM=MF=CN=x,AF=6-2x,ME=6-x,然后表示出S1、S2,结合2S1=3S2就可求得x的值,进而得到CE的值.
16.【答案】2
【解析】【解答】解:如图,连接AC、CF,
在正方形ABCD和正方形CEFG中,AC= BC=2 ,CF= CE=6 ,
∠ACD=∠GCF=45°,
所以,∠ACF=45°+45°=90°,
所以,△ACF是直角三角形,
由勾股定理得,AF=
=
=4 ,
∵H是AF的中点,
∴CH= AF= ×4 =2 .
故答案为2 .
【分析】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,难点在于作辅助线构造出直角三角形.连接AC、CF,根据正方形的性质求出AC、CF,并判断出△ACF是直角三角形,再利用勾股定理列式求出AF,然后根据直角三角形斜边上的中线等于斜边的一半解答.
17.【答案】证明:∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
同理 .
∴ ,
∵ ,
∴ 且 ,
∴四边形 是平行四边形,
∵ ,
∴四边形 是菱形.
【解析】【分析】由角平分线和平行线的性质先证出 , ,从而有 ,得到四边形 是平行四边形,又因为 ,所以四边形 是菱形.
18.【答案】证明:连接AC,
在△ADB和△CBD中,
∵ ,
∴△ADB≌△CBD(SSS),
∴∠DCA=∠CAB,∠DAC=∠ACB,
∴AB∥CD,AD∥BC.
【解析】【分析】连接AC,利用三边对应相等的两个三角形全等,证明△ADB≌△CBD,再利用全等的性质可得∠DCA=∠CAB,∠DAC=∠ACB,进而证明AB∥CD,AD∥BC.
19.【答案】证明:证法一:∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=90°.
在△ABE和△CDF中
∵ , ∴△ABE≌△CDF(SAS),
∴BE=DF(全等三角形对应边相等)
证法二:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵AE=CF,∴AD-AE=BC-CF
即ED=BF,
而ED∥BF,
∴四边形BFDE为平行四边形
∴BE=DF(平行四边形对边相等).
利用全等三角形对应边相等求证
【解析】【分析】证法一利用三角形全等来证明对应边相等;证法二利用矩形的性质及AE=CF证得四边形BFDE为平行四边形,进而利用平行四边形对边相等证得BE=DF.
20.【答案】证明:(1)∵BE、BF分别是△ABC中∠B及它的外角的平分线,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵AE⊥BE,E为垂足,AF⊥BF,F为垂足,
∴∠AFB=∠AEB=90°,
∴四边形AEBF为矩形;
(2)∵四边形AEBF为矩形,
∴BM=MA=ME,
∴∠2=∠5,
∵∠2=∠1,
∴∠1=∠5,
∴ME∥BC,
∵M是AB的中点,
∴N为AC的中点,
∴MN=BC.
【解析】【分析】(1)由BE、BE是角平分线可得∠EBF是90°,进而由条件中的两个垂直可得两个直角,可得四边形AEBF是矩形;
(2)由矩形的F质可得∠2=∠5进而利用角平分线的性质可得∠1=∠5,可得ME∥BC,进而可得N为AC中点,根据三角形中位线性质求出即可.
21.【答案】(1)证明:∵AD是△ABC的中线,∴BD=CD,∵AE∥BC,∴∠AEF=∠DBF,在△AFE和△DFB中,,∴△AFE≌△DFB(AAS),∴AE=BD,∴AE=CD,∵AE∥BC,∴四边形ADCE是平行四边形;(2)当AB=AC时,四边形ADCE是矩形;∵AB=AC,AD是△ABC的中线,∴AD⊥BC,∴∠ADC=90°,∵四边形ADCE是平行四边形,∴四边形ADCE是矩形,故答案为:AB=AC;(3)当AB⊥AC,AB=AC时,四边形ADCE是正方形,∵AB⊥AC,AB=AC,∴△ABC是等腰直角三角形,∵AD是△ABC的中线,∴AD=CD,AD⊥BC,又∵四边形ADCE是平行四边形,∴四边形ADCE是正方形,故答案为:AB⊥AC,AB=AC.
【解析】【分析】(1)首先证明△AFE≌△DFB可得AE=BD,进而可证明AE=CD,再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;
(2)当AB=AC时,根据等腰三角形三线合一可得AD⊥BC,再根据有一个角是直角的平行四边形是矩形可得结论;
(3)当AB=AC,AB⊥AC时,△ABC是等腰直角三角形,根据直角三角形斜边上的中线等于斜边的一半可得AD=CD,根据等腰三角形的性质可得AD⊥BC,从而可得证明四边形ADCE是正方形.
22.【答案】证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵∠CDE=∠DCE,
∴DE=CE,
在Rt△DAE和Rt△CBE中, ,
∴Rt△DAE≌Rt△CBE(HL),
∴AE=BE
【解析】【分析】证出DE=CE,由HL证明Rt△DAE≌Rt△CBE,得出对应边相等即可.
23.【答案】6
【解析】【解答】解 :如图,取BC的中点G,连接DG、EG、FG.
∵ AD∶BC=1∶2 ;G是BC的中点,
∴ BG=AD ;
又∵AD//BC ;
∴四边形ABGD是平行四边形;
∴S△ADE+S△BEG=S平行四边形ABDG
S△AFD+S△BG=S平行四边形ABDG
∴上面两个三角形的面积差与下面两个三角形面积差相等。
∵上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍。
下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12
∴S△AOF=12÷2=6m2.
【分析】如图,取BC的中点G,连接DG、EG、FG.根据一组对边平行且相等的四边形是平行四边形得出四边形ABGD是平行四边形; 根据平行四边形的面积公式,三角形的面积计算公式得出S△ADE+S△BEG=S平行四边形ABDG,S△AFD+S△BG=S平行四边形ABDG;从而得出上面两个三角形的面积差与下面两个三角形面积差相等;进而得出上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍;下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12;从而得出答案。
24.【答案】(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,
∴BD⊥CG,
∵AB=AD=2,在Rt△ABD中,DB= ,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA= ,
即OG=OA+AG= + =2 ,
∴EB=GD= .
【解析】【分析】(1)在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,得到∠GAD=∠EAB从而△GAD≌△EAB,即EB=GD;(2)EB⊥GD,由(1)得∠ADG=∠ABE则在△BDH中,∠DHB=90°所以EB⊥GD;(3)设BD与AC交于点O,由AB=AD=2在Rt△ABD中求得DB,所以得到结果.
