2022-2023学年八年级数学下册人教版第十八章 平行四边形 能力提升检测卷 (无答案)
文档属性
| 名称 | 2022-2023学年八年级数学下册人教版第十八章 平行四边形 能力提升检测卷 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 00:00:00 | ||
图片预览

文档简介
第十八章 平行四边形 能力提升检测卷 2022-2023年八年级数学下册人教版
一、单选题
1.下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相垂直平分的四边形是正方形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等且互相平分的四边形是矩形
2.一个菱形的两条对角线分别为 和 ,则这个菱形的面积是( )
A. B. C. D.
3.如图,在中,DE平分,,则( )
A.30° B.45° C.60° D.80°
4.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
5.如图在 的正方形网格中, AB,AC是经过格点的线段,如果能找到这样的格点M,使得S△ACM=S△ABM,这样的点M的个数是 ( )
A.1 B.2 C.3 D.4
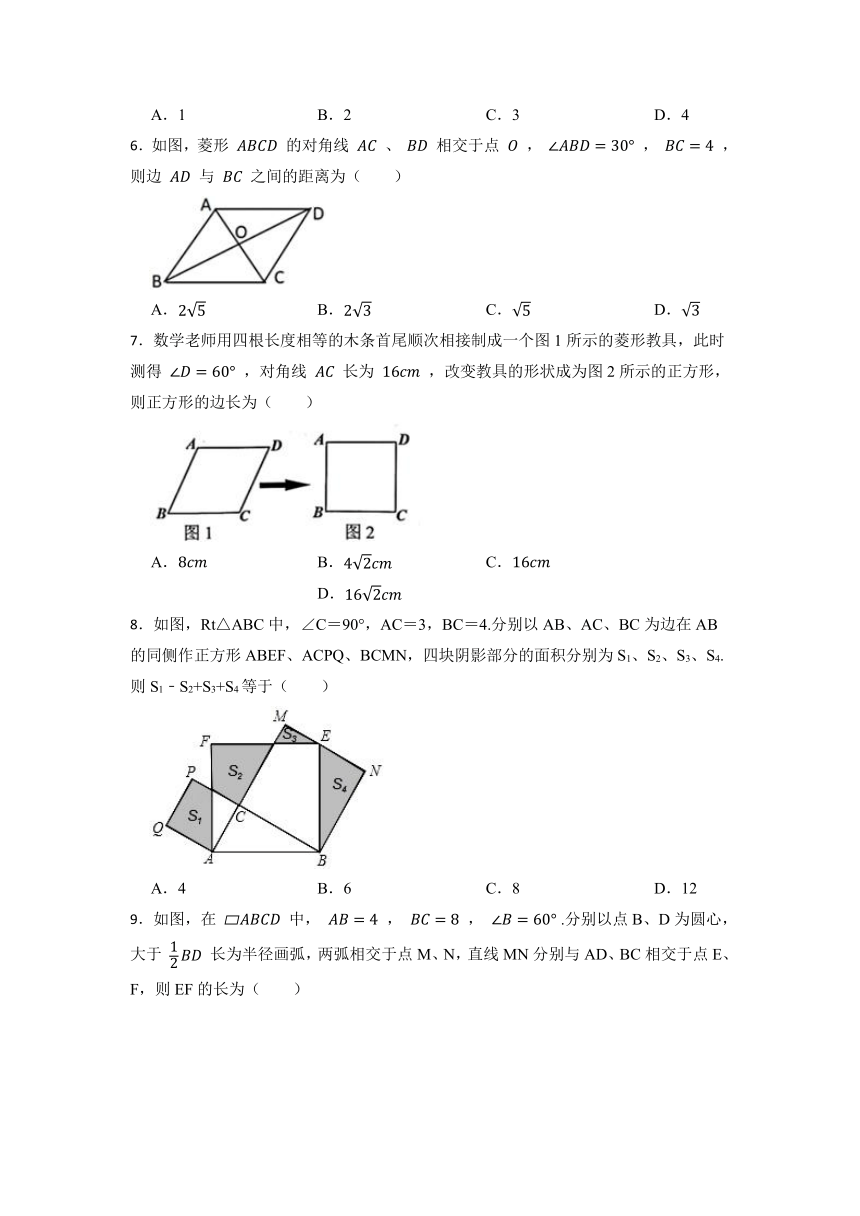
6.如图,菱形 的对角线 、 相交于点 , , ,则边 与 之间的距离为( )
A. B. C. D.
7.数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得 ,对角线 长为 ,改变教具的形状成为图2所示的正方形,则正方形的边长为( )
A. B. C. D.
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于( )
A.4 B.6 C.8 D.12
9.如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( )
A. B.4 C. D.
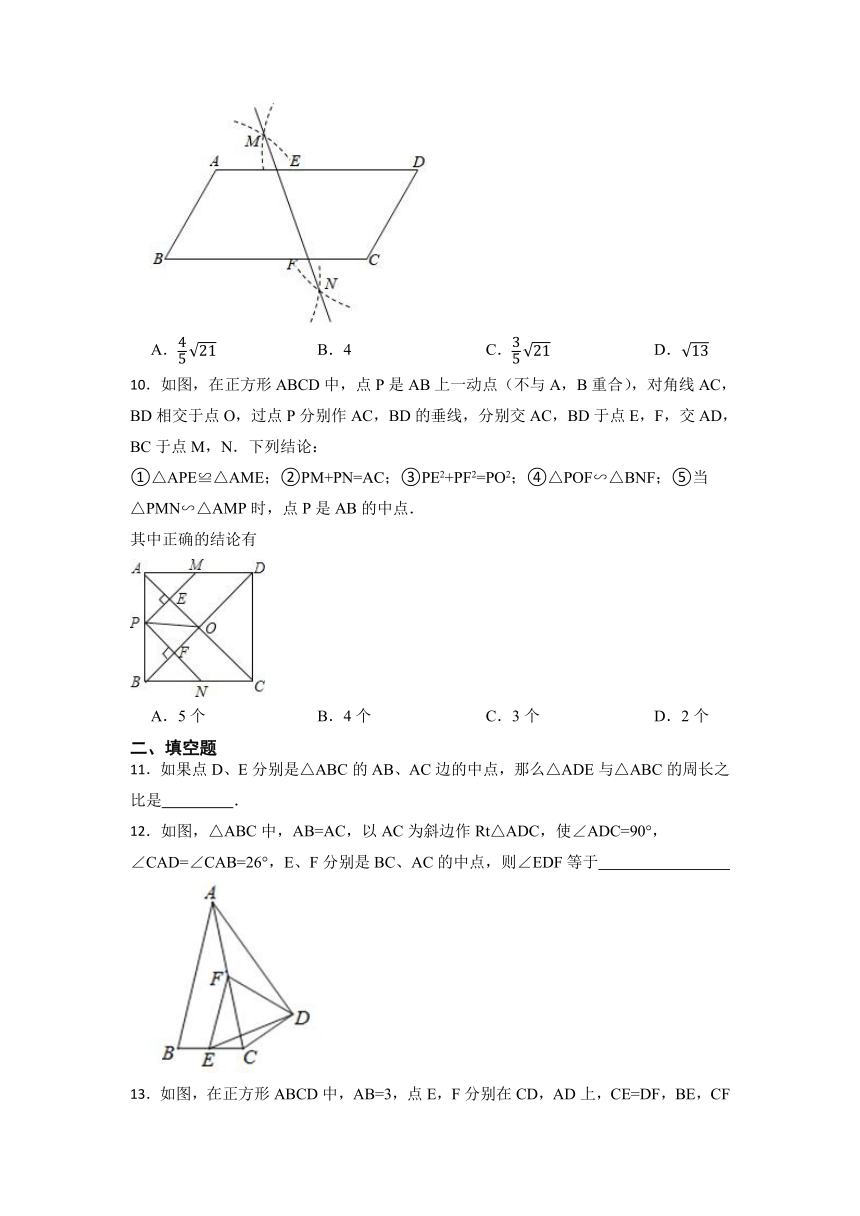
10.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
A.5个 B.4个 C.3个 D.2个
二、填空题
11.如果点D、E分别是△ABC的AB、AC边的中点,那么△ADE与△ABC的周长之比是 .
12.如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于
13.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为 .
14.在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .
15.如图,在边长为10的菱形ABCD中,对角线BD =16. 点E是AB的中点,P、Q是BD上的动点,且始终保持PQ =2, 则四边形AEPQ周长的最小值为 .(结果保留根号)
三、解答题
16.如图所示,平行四边形ABCD中,E、F是对角线BD上两点,连接AE、AF、CE、CF,添加一个什么条件,可使四边形AECF是平行四边形?并给出证明.
17.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.求证:四边形BCFE是菱形.
18.如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.
19.如图,四边形 是平行四边形, 、 在对角线 上,且 ,连接 , , , .求证 .
20.如图,在△ABC中,M、N分别是BC与EF的中点,CF⊥AB,BE⊥AC.求证:MN⊥EF.
21.如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
22.如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且∠ABE=∠CDF.
求证:四边形BEDF是平行四边形.
23.如图,已知平行四边形ABCD中,∠ABC、∠ADC的角平分线分别交AD、BC于点E、F.求证:DE=BF.
24.如图,△ABC中,∠ACB=90°,D为AB中点,四边形BCED为平行四边形.DE、AC相交于点F.
(1)求证:点F为AC中点;
(2)试确定四边形ADCE的形状,并说明理由;
(3)若四边形ADCE为正方形,△ABC应添加什么条件,并证明你的结论.
25.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
26.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
一、单选题
1.下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相垂直平分的四边形是正方形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等且互相平分的四边形是矩形
2.一个菱形的两条对角线分别为 和 ,则这个菱形的面积是( )
A. B. C. D.
3.如图,在中,DE平分,,则( )
A.30° B.45° C.60° D.80°
4.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
5.如图在 的正方形网格中, AB,AC是经过格点的线段,如果能找到这样的格点M,使得S△ACM=S△ABM,这样的点M的个数是 ( )
A.1 B.2 C.3 D.4
6.如图,菱形 的对角线 、 相交于点 , , ,则边 与 之间的距离为( )
A. B. C. D.
7.数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得 ,对角线 长为 ,改变教具的形状成为图2所示的正方形,则正方形的边长为( )
A. B. C. D.
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于( )
A.4 B.6 C.8 D.12
9.如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( )
A. B.4 C. D.
10.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
A.5个 B.4个 C.3个 D.2个
二、填空题
11.如果点D、E分别是△ABC的AB、AC边的中点,那么△ADE与△ABC的周长之比是 .
12.如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于
13.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为 .
14.在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .
15.如图,在边长为10的菱形ABCD中,对角线BD =16. 点E是AB的中点,P、Q是BD上的动点,且始终保持PQ =2, 则四边形AEPQ周长的最小值为 .(结果保留根号)
三、解答题
16.如图所示,平行四边形ABCD中,E、F是对角线BD上两点,连接AE、AF、CE、CF,添加一个什么条件,可使四边形AECF是平行四边形?并给出证明.
17.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.求证:四边形BCFE是菱形.
18.如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.
19.如图,四边形 是平行四边形, 、 在对角线 上,且 ,连接 , , , .求证 .
20.如图,在△ABC中,M、N分别是BC与EF的中点,CF⊥AB,BE⊥AC.求证:MN⊥EF.
21.如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
22.如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且∠ABE=∠CDF.
求证:四边形BEDF是平行四边形.
23.如图,已知平行四边形ABCD中,∠ABC、∠ADC的角平分线分别交AD、BC于点E、F.求证:DE=BF.
24.如图,△ABC中,∠ACB=90°,D为AB中点,四边形BCED为平行四边形.DE、AC相交于点F.
(1)求证:点F为AC中点;
(2)试确定四边形ADCE的形状,并说明理由;
(3)若四边形ADCE为正方形,△ABC应添加什么条件,并证明你的结论.
25.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
26.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
