2022—2023学年北师大版数学九年级下册1.5 三角函数的应用 同步练习(含解析)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级下册1.5 三角函数的应用 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 711.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 19:53:08 | ||
图片预览

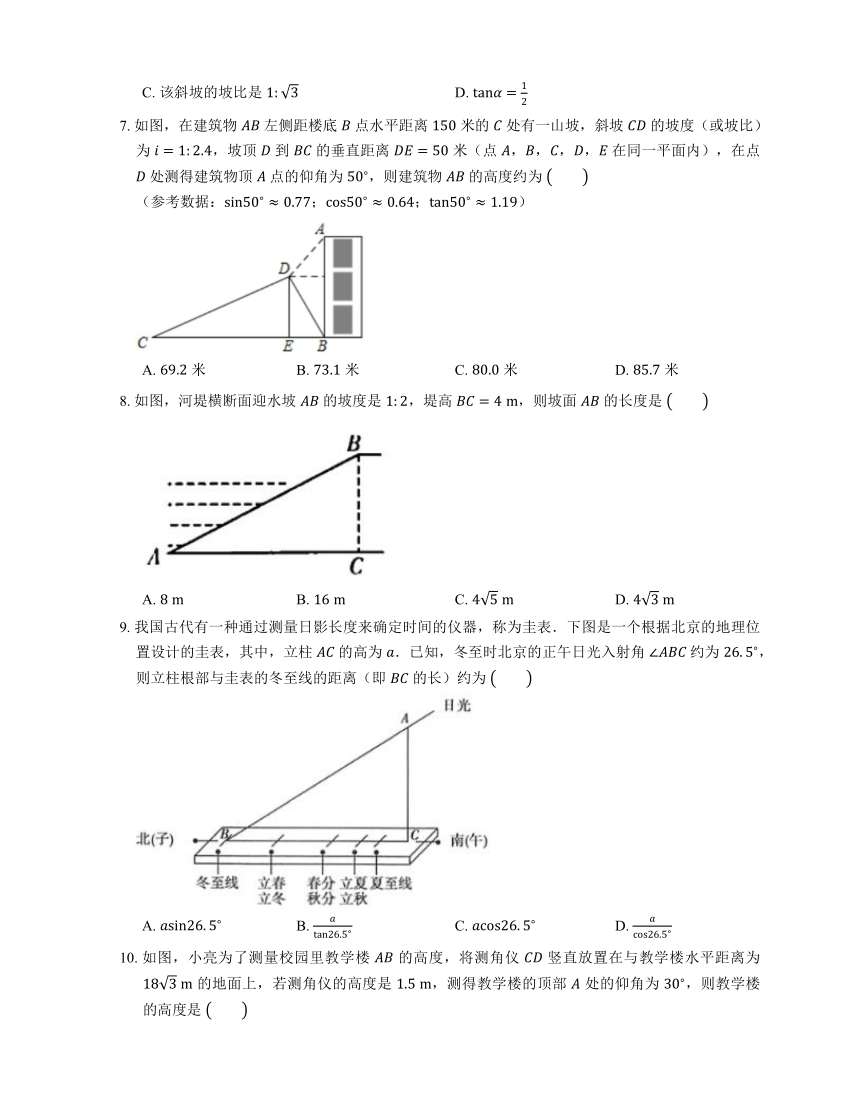
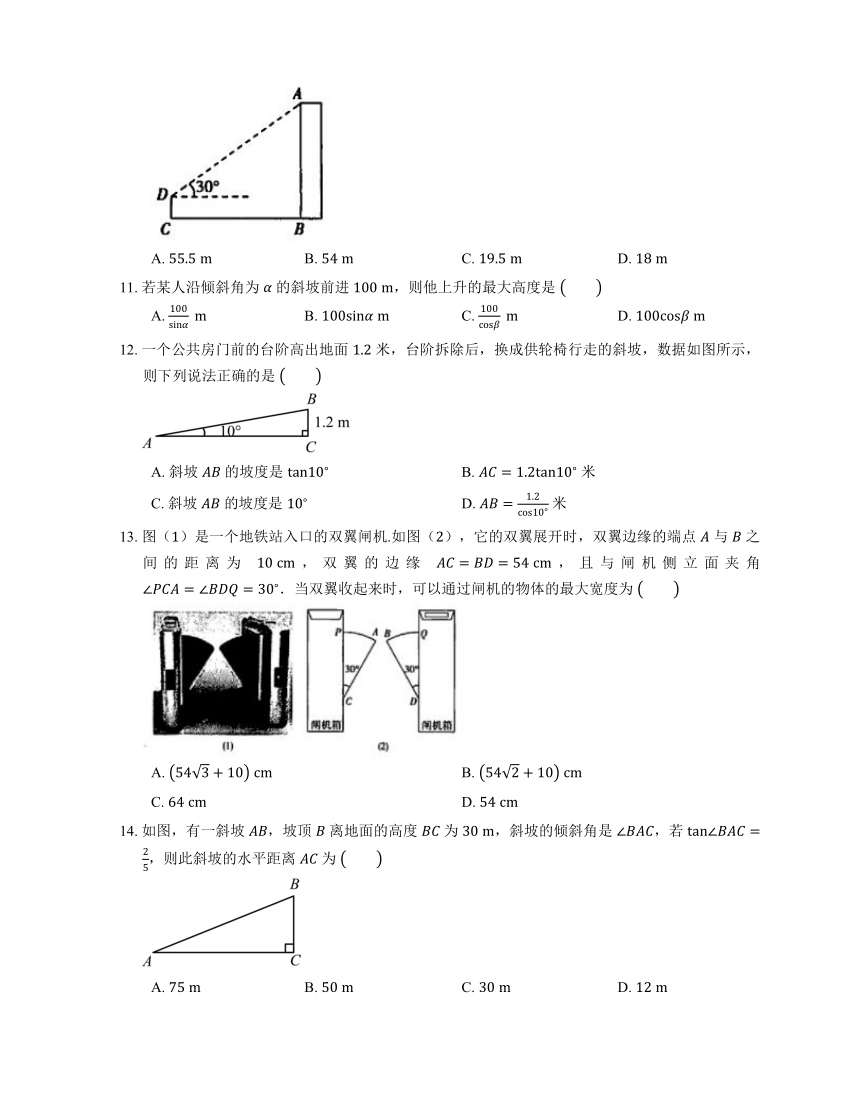
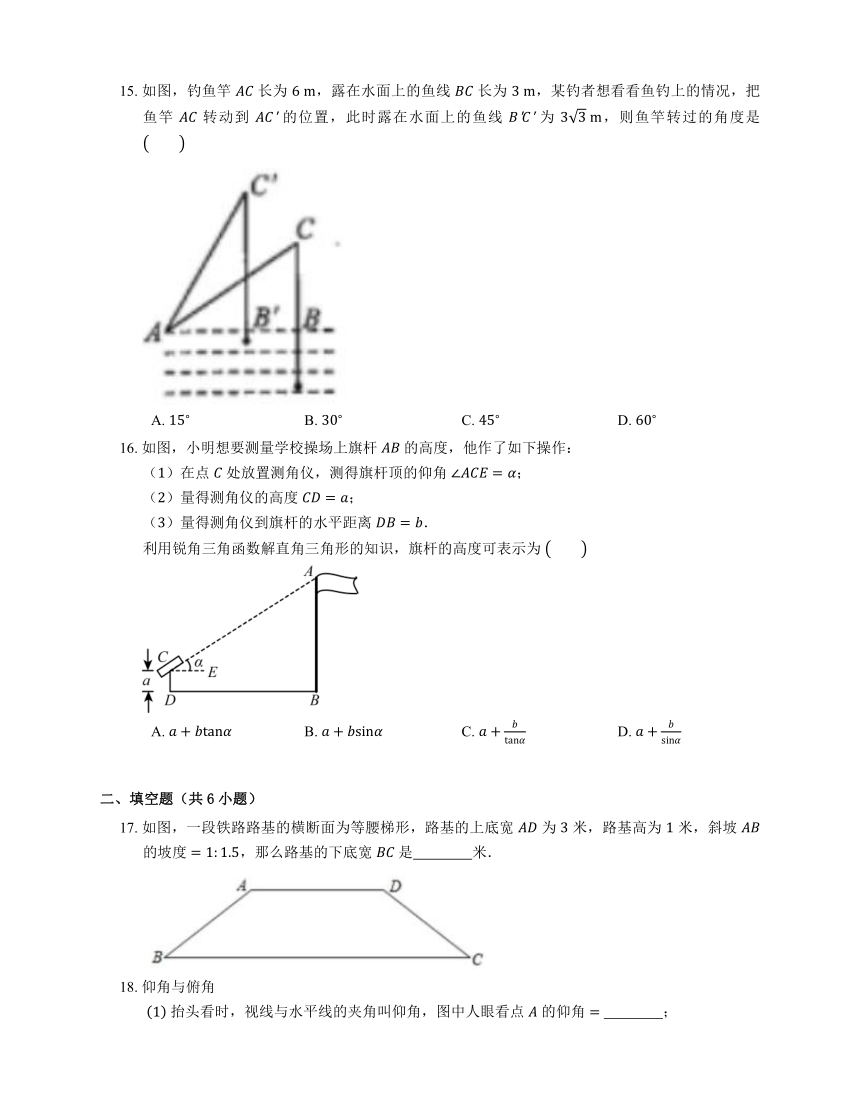

文档简介
北师大版九下 1.5 三角函数的应用
一、选择题(共16小题)
1. 小新站在高楼上的点 处看一棵小树顶端 的仰角为 ,同时看小树底端 的俯角为 ,则 等于
A. B. C. D.
2. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
3. 如图,从点 观测点 的仰角是
A. B. C. D.
4. 如图,有一斜坡 ,坡顶 离地面的高度 为 ,斜坡的倾斜角是 ,若 ,则此斜坡的水平距离 为
A. B. C. D.
5. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
6. 如图,一个斜坡长为 米,坡顶离水平地面的距离为 米,,则下列说法正确的是
A. 该斜坡的坡度是 B. 该斜坡的坡比是
C. 该斜坡的坡比是 D.
7. 如图,在建筑物 左侧距楼底 点水平距离 米的 处有一山坡,斜坡 的坡度(或坡比)为 ,坡顶 到 的垂直距离 米(点 ,,,, 在同一平面内),在点 处测得建筑物顶 点的仰角为 ,则建筑物 的高度约为
(参考数据:;;)
A. 米 B. 米 C. 米 D. 米
8. 如图,河堤横断面迎水坡 的坡度是 ,堤高 ,则坡面 的长度是
A. B. C. D.
9. 我国古代有一种通过测量日影长度来确定时间的仪器,称为圭表.下图是一个根据北京的地理位置设计的圭表,其中,立柱 的高为 .已知,冬至时北京的正午日光入射角 约为 ,则立柱根部与圭表的冬至线的距离(即 的长)约为
A. B. C. D.
10. 如图,小亮为了测量校园里教学楼 的高度,将测角仪 竖直放置在与教学楼水平距离为 的地面上,若测角仪的高度是 ,测得教学楼的顶部 处的仰角为 ,则教学楼的高度是
A. B. C. D.
11. 若某人沿倾斜角为 的斜坡前进 ,则他上升的最大高度是
A. B. C. D.
12. 一个公共房门前的台阶高出地面 米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列说法正确的是
A. 斜坡 的坡度是 B. 米
C. 斜坡 的坡度是 D. 米
13. 图()是一个地铁站入口的双翼闸机.如图(),它的双翼展开时,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机侧立面夹角 .当双翼收起来时,可以通过闸机的物体的最大宽度为
A. B.
C. D.
14. 如图,有一斜坡 ,坡顶 离地面的高度 为 ,斜坡的倾斜角是 ,若 ,则此斜坡的水平距离 为
A. B. C. D.
15. 如图,钓鱼竿 长为 ,露在水面上的鱼线 长为 ,某钓者想看看鱼钓上的情况,把鱼竿 转动到 的位置,此时露在水面上的鱼线 为 ,则鱼竿转过的角度是
A. B. C. D.
16. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:
()在点 处放置测角仪,测得旗杆顶的仰角 ;
()量得测角仪的高度 ;
()量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
二、填空题(共6小题)
17. 如图,一段铁路路基的横断面为等腰梯形,路基的上底宽 为 米,路基高为 米,斜坡 的坡度 ,那么路基的下底宽 是 米.
18. 仰角与俯角
抬头看时,视线与水平线的夹角叫仰角,图中人眼看点 的仰角 ;
低头看时,视线与水平线的夹角叫俯角,图中人眼看点 的俯角 .
19. 如果在 点处观察 点的仰角为 ,那么在 点处观察 点的俯角为 (用含 的式子表示).
20. 如果一个斜坡的坡度 ,那么该斜坡的坡角为 度.
21. 已知某小山坡的坡长为 米、山坡的高度为 米,那么该山坡的坡度 .
22. 小明同学逛书城,从地面一楼乘自动扶梯,随扶梯移动了 米,到达距离地面 米高的二楼,则该自动扶梯的坡度 .
三、解答题(共5小题)
23. 如图,为了测量建筑物 的高度,先从与建筑物 的底部 点水平相距 米的点 处出发,沿斜坡 行走至坡顶 处,斜坡 的坡度 ,坡顶 到 的距离 米,在点 处测得建筑物顶端 点的仰角为 ,点 ,,,, 在同一平面内,根据测量数据,请计算建筑物 的高度(结果精确到 米).(参考数据:,,)
24. 如图是某校体育场内一看台的截面图,看台 与水平线的夹角为 ,最低处 与地面的距离 为 米,在 , 正前方有垂直于地面的旗杆 ,在 , 两处测得旗杆顶端 的仰角分别为 和 , 长为 米,升旗仪式中,当国歌开始播放时,国旗也在离地面 米的 处同时冉冉升起,国歌播放结束时,国旗刚好上升到旗杆顶端 ,已知国歌播放时间为 秒,求国旗上升的平均速度.(结果精确到 米/秒)
25. 如图所示,课外活动中,小明在离旗杆 米的 处,用测角仪测得旗杆顶部 的仰角为 ,已知测角仪器的高 米,求旗杆 的高.(精确到 米)
(供选用的数据:,,)
26. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比) 的山坡 上发现一棵古树 ,测得古树底端 到山脚点 的距离 ,在距山脚点 处水平距离 的点 处测得古树顶端 的仰角 (古树 与山坡 的剖面、点 在同一平面上,古树 所在直线与直线 垂直),则古树 的高度约为多少米 (结果精确到整数)(数据 ,,)
27. 如图,某校的实验楼对面是一幢教学楼,小张在实验楼的窗口 处测得教学楼顶部 的仰角为 ,教学楼底部 的俯角为 ,量得实验楼与教学楼之间的距离 米.求教学楼 的高度(精确到 米).
(参考数据:,,,,,)
答案
1. B
2. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
3. B
【解析】 从点 观测点 的视线是 ,水平线是 ,
从点 观测点 的仰角是 .
4. A
【解析】,,,
,
解得,.
5. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
6. C
7. D
【解析】 斜坡 的坡度(或坡比)为 ,
,
米,
米,
米,
米,
米.
故选:D.
8. C
9. B
【解析】因为 ,
所以 .
10. C
【解析】过 作 ,
在 处测得旗杆顶端 的仰角为 ,
,
,
,
.
11. B
12. A
13. C
【解析】如图所示,过 作 于 , 过 作 于 ,
则 中,.同理可得 ,又
点 与点 之间的距离为 ,
通过闸机的物体的最大宽度为 .
14. A
【解析】,,,
,
.
15. B
16. A 【解析】过 作 于 ,则四边形 是矩形.
,,
,
,
,
.
17.
【解析】如图,过 作 ,过 作 ,
米, 米,
坡度 ,
米,
米.
故答案为 .
18. ,
19.
【解析】如图所示:
在 点处观察 点的仰角为 ,即 ,
,
,
在 点处观察 点的俯角为 .
20.
【解析】,
坡角 .
故答案为 .
21.
【解析】由勾股定理可知山坡的水平距离为: 米,
坡度 .
22.
【解析】如图,
根据题意知: 米, 米,
(米),
该自动扶梯的坡度 ,
该自动扶梯的坡度 .
23. 因为斜坡 的坡度(或坡比)为 ,
所以 ,
因为 米,
所以 米,
因为 米,
所以 (米),
所以 (米).
答:建筑物 的高度为 米.
24. 依题意得 ,.
在 中,.
在 中,.
.
.
答:国旗上升的平均速度约为 米/秒.
25. ,,,
四边形 是矩形,
米,
在 中,
米,,
(米),
(米).
答:旗杆 的高是 米.
26. 延长 交 的延长线于点 ,则 ,
山坡 上坡度 ,
令 ,则 ,
在 中,由勾股定理得,,
,
解得 ,
,,
,
在 中,,
,
,
古树 的高度约为 .
27. 过点 作 ,垂足为点 ,
由题意,得 ,,(米),
在 中,
,
,
在 中,
,
,
(米).
答:教学楼 的高度约为 米.
一、选择题(共16小题)
1. 小新站在高楼上的点 处看一棵小树顶端 的仰角为 ,同时看小树底端 的俯角为 ,则 等于
A. B. C. D.
2. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
3. 如图,从点 观测点 的仰角是
A. B. C. D.
4. 如图,有一斜坡 ,坡顶 离地面的高度 为 ,斜坡的倾斜角是 ,若 ,则此斜坡的水平距离 为
A. B. C. D.
5. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
6. 如图,一个斜坡长为 米,坡顶离水平地面的距离为 米,,则下列说法正确的是
A. 该斜坡的坡度是 B. 该斜坡的坡比是
C. 该斜坡的坡比是 D.
7. 如图,在建筑物 左侧距楼底 点水平距离 米的 处有一山坡,斜坡 的坡度(或坡比)为 ,坡顶 到 的垂直距离 米(点 ,,,, 在同一平面内),在点 处测得建筑物顶 点的仰角为 ,则建筑物 的高度约为
(参考数据:;;)
A. 米 B. 米 C. 米 D. 米
8. 如图,河堤横断面迎水坡 的坡度是 ,堤高 ,则坡面 的长度是
A. B. C. D.
9. 我国古代有一种通过测量日影长度来确定时间的仪器,称为圭表.下图是一个根据北京的地理位置设计的圭表,其中,立柱 的高为 .已知,冬至时北京的正午日光入射角 约为 ,则立柱根部与圭表的冬至线的距离(即 的长)约为
A. B. C. D.
10. 如图,小亮为了测量校园里教学楼 的高度,将测角仪 竖直放置在与教学楼水平距离为 的地面上,若测角仪的高度是 ,测得教学楼的顶部 处的仰角为 ,则教学楼的高度是
A. B. C. D.
11. 若某人沿倾斜角为 的斜坡前进 ,则他上升的最大高度是
A. B. C. D.
12. 一个公共房门前的台阶高出地面 米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列说法正确的是
A. 斜坡 的坡度是 B. 米
C. 斜坡 的坡度是 D. 米
13. 图()是一个地铁站入口的双翼闸机.如图(),它的双翼展开时,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机侧立面夹角 .当双翼收起来时,可以通过闸机的物体的最大宽度为
A. B.
C. D.
14. 如图,有一斜坡 ,坡顶 离地面的高度 为 ,斜坡的倾斜角是 ,若 ,则此斜坡的水平距离 为
A. B. C. D.
15. 如图,钓鱼竿 长为 ,露在水面上的鱼线 长为 ,某钓者想看看鱼钓上的情况,把鱼竿 转动到 的位置,此时露在水面上的鱼线 为 ,则鱼竿转过的角度是
A. B. C. D.
16. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:
()在点 处放置测角仪,测得旗杆顶的仰角 ;
()量得测角仪的高度 ;
()量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
二、填空题(共6小题)
17. 如图,一段铁路路基的横断面为等腰梯形,路基的上底宽 为 米,路基高为 米,斜坡 的坡度 ,那么路基的下底宽 是 米.
18. 仰角与俯角
抬头看时,视线与水平线的夹角叫仰角,图中人眼看点 的仰角 ;
低头看时,视线与水平线的夹角叫俯角,图中人眼看点 的俯角 .
19. 如果在 点处观察 点的仰角为 ,那么在 点处观察 点的俯角为 (用含 的式子表示).
20. 如果一个斜坡的坡度 ,那么该斜坡的坡角为 度.
21. 已知某小山坡的坡长为 米、山坡的高度为 米,那么该山坡的坡度 .
22. 小明同学逛书城,从地面一楼乘自动扶梯,随扶梯移动了 米,到达距离地面 米高的二楼,则该自动扶梯的坡度 .
三、解答题(共5小题)
23. 如图,为了测量建筑物 的高度,先从与建筑物 的底部 点水平相距 米的点 处出发,沿斜坡 行走至坡顶 处,斜坡 的坡度 ,坡顶 到 的距离 米,在点 处测得建筑物顶端 点的仰角为 ,点 ,,,, 在同一平面内,根据测量数据,请计算建筑物 的高度(结果精确到 米).(参考数据:,,)
24. 如图是某校体育场内一看台的截面图,看台 与水平线的夹角为 ,最低处 与地面的距离 为 米,在 , 正前方有垂直于地面的旗杆 ,在 , 两处测得旗杆顶端 的仰角分别为 和 , 长为 米,升旗仪式中,当国歌开始播放时,国旗也在离地面 米的 处同时冉冉升起,国歌播放结束时,国旗刚好上升到旗杆顶端 ,已知国歌播放时间为 秒,求国旗上升的平均速度.(结果精确到 米/秒)
25. 如图所示,课外活动中,小明在离旗杆 米的 处,用测角仪测得旗杆顶部 的仰角为 ,已知测角仪器的高 米,求旗杆 的高.(精确到 米)
(供选用的数据:,,)
26. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比) 的山坡 上发现一棵古树 ,测得古树底端 到山脚点 的距离 ,在距山脚点 处水平距离 的点 处测得古树顶端 的仰角 (古树 与山坡 的剖面、点 在同一平面上,古树 所在直线与直线 垂直),则古树 的高度约为多少米 (结果精确到整数)(数据 ,,)
27. 如图,某校的实验楼对面是一幢教学楼,小张在实验楼的窗口 处测得教学楼顶部 的仰角为 ,教学楼底部 的俯角为 ,量得实验楼与教学楼之间的距离 米.求教学楼 的高度(精确到 米).
(参考数据:,,,,,)
答案
1. B
2. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
3. B
【解析】 从点 观测点 的视线是 ,水平线是 ,
从点 观测点 的仰角是 .
4. A
【解析】,,,
,
解得,.
5. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
6. C
7. D
【解析】 斜坡 的坡度(或坡比)为 ,
,
米,
米,
米,
米,
米.
故选:D.
8. C
9. B
【解析】因为 ,
所以 .
10. C
【解析】过 作 ,
在 处测得旗杆顶端 的仰角为 ,
,
,
,
.
11. B
12. A
13. C
【解析】如图所示,过 作 于 , 过 作 于 ,
则 中,.同理可得 ,又
点 与点 之间的距离为 ,
通过闸机的物体的最大宽度为 .
14. A
【解析】,,,
,
.
15. B
16. A 【解析】过 作 于 ,则四边形 是矩形.
,,
,
,
,
.
17.
【解析】如图,过 作 ,过 作 ,
米, 米,
坡度 ,
米,
米.
故答案为 .
18. ,
19.
【解析】如图所示:
在 点处观察 点的仰角为 ,即 ,
,
,
在 点处观察 点的俯角为 .
20.
【解析】,
坡角 .
故答案为 .
21.
【解析】由勾股定理可知山坡的水平距离为: 米,
坡度 .
22.
【解析】如图,
根据题意知: 米, 米,
(米),
该自动扶梯的坡度 ,
该自动扶梯的坡度 .
23. 因为斜坡 的坡度(或坡比)为 ,
所以 ,
因为 米,
所以 米,
因为 米,
所以 (米),
所以 (米).
答:建筑物 的高度为 米.
24. 依题意得 ,.
在 中,.
在 中,.
.
.
答:国旗上升的平均速度约为 米/秒.
25. ,,,
四边形 是矩形,
米,
在 中,
米,,
(米),
(米).
答:旗杆 的高是 米.
26. 延长 交 的延长线于点 ,则 ,
山坡 上坡度 ,
令 ,则 ,
在 中,由勾股定理得,,
,
解得 ,
,,
,
在 中,,
,
,
古树 的高度约为 .
27. 过点 作 ,垂足为点 ,
由题意,得 ,,(米),
在 中,
,
,
在 中,
,
,
(米).
答:教学楼 的高度约为 米.
