2022-2023年度华东师大版八年级年级数学下册第17章函数及其图像单元检测卷(附答案解析)
文档属性
| 名称 | 2022-2023年度华东师大版八年级年级数学下册第17章函数及其图像单元检测卷(附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 22:27:07 | ||
图片预览




文档简介
第17章 函数及其图像 单元检测卷 2022-2023年度八年级年级数学下册华师大版
一、单选题
1.一次函数 的图象只经过第一、三象限,则( )
A.k>0 B.k<0 C.b>0 D.b<0
2.已知一次函数y=ax﹣6与y=bx﹣2的图象在x轴上相交于同一点,则 的值是( )
A.4 B.﹣3 C.﹣ D.
3.如图,点A(-2,1)到y轴的距离为( )
A.-2 B.1 C.2 D.
4.如图,已知反比例函数y= 与正比例函数y=kx(k<0)的图象相交于A、B两点,AC垂直x轴于C,则△ABC的面积为( )
A.3 B.2 C.k D.k2
5.函数y=(x﹣1)0中,自变量x的取值范围是( )
A.x>1 B.x≠1 C.x<1 D.x≥1
6.下列不能确定点的位置的是( )
A.东经,北纬
B.礼堂6排22号
C.地下车库负二层
D.港口南偏东方向上距港口10海里
7.如果一次函数y=kx+b中自变量x的取值范围是-1≤x≤3时,函数值y的取值范围是1≤y≤3,这个一次函数解析式是()
A.y=x+或y=-x+ B.y=x+
C.y=-x+ D.y=x-
8.如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC,BC边上,C,D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
A. B.
C. D.
9.如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A.6 B.10 C.2 D.2
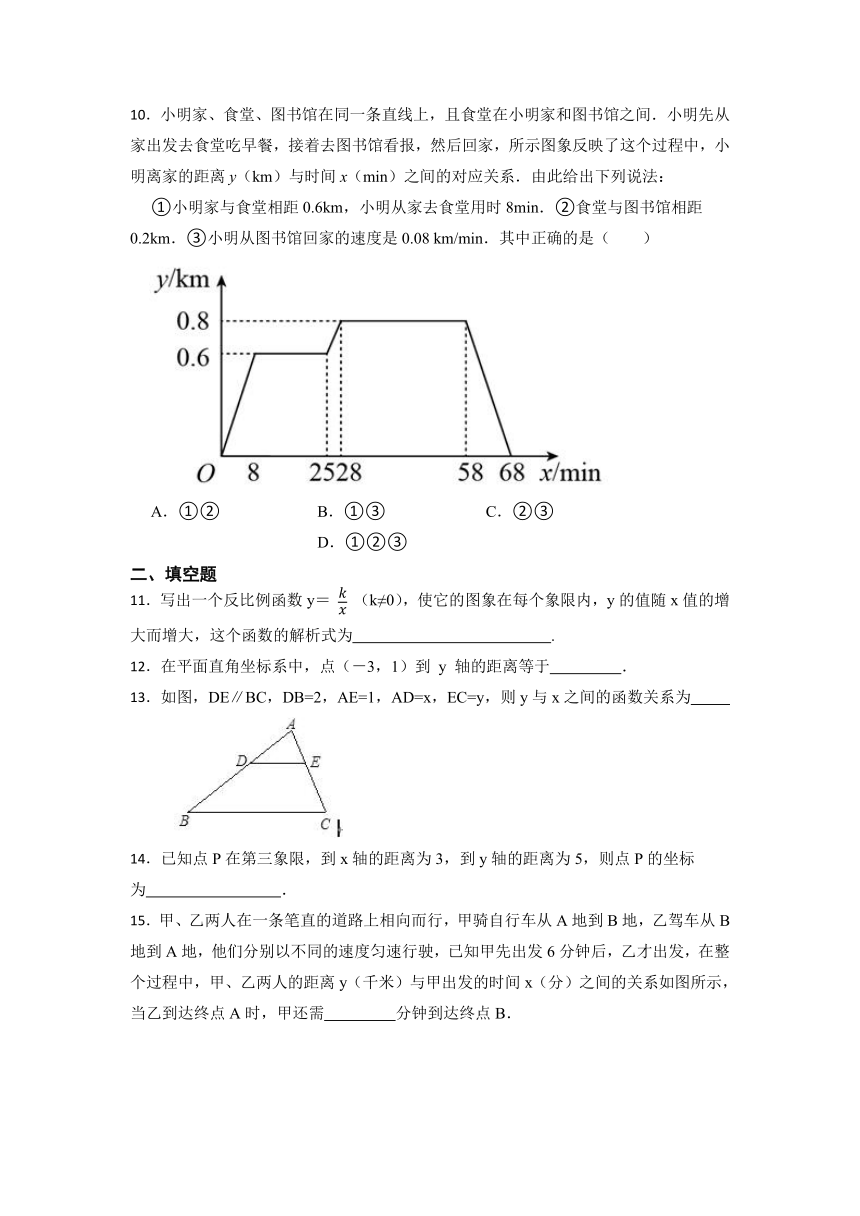
10.小明家、食堂、图书馆在同一条直线上,且食堂在小明家和图书馆之间.小明先从家出发去食堂吃早餐,接着去图书馆看报,然后回家,所示图象反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系.由此给出下列说法:
①小明家与食堂相距0.6km,小明从家去食堂用时8min.②食堂与图书馆相距0.2km.③小明从图书馆回家的速度是0.08 km/min.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
11.写出一个反比例函数y= (k≠0),使它的图象在每个象限内,y的值随x值的增大而增大,这个函数的解析式为 .
12.在平面直角坐标系中,点(-3,1)到 y 轴的距离等于 .
13.如图,DE∥BC,DB=2,AE=1,AD=x,EC=y,则y与x之间的函数关系为
14.已知点P在第三象限,到x轴的距离为3,到y轴的距离为5,则点P的坐标为 .
15.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.
三、解答题
16.一次函数的图象经过A(3,4)和点B(2,7),求此一次函数的表达式.
17.已知y与3x+1成正比例,且x=3时,y=4.求y与x之间的函数关系式.
18.小丽一家利用元旦三天驾车到某景点旅游。小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
19.在平面直角坐标系中,已知A(,1),B(2,0),O(0,0),反比例函数y=的图象经过点A.
(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,点B与点D对应,试判断点D是否在该反比例函数的图象上.
20.直线 与反比例函数 (其中 )的图象交于 、 ,求点 的坐标.
21.说明:在解答“结论应用”时,从A,B两题中任选一题作答.
问题探究:
启知学习小组在课外学习时,发现了这样一个问题:如图①,在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图①中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
结论应用:
在平面直角坐标系中,反比例函数y= (x≠0)的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(1)A
Ⅰ.求反比例函数的表达式;
Ⅱ.如图②,已知b=1,AC,BD相交于点E,求证:CD∥AB.
(2)B
Ⅰ.求反比例函数的表达式;
Ⅱ.如图③,若点B在第三象限,判断并证明CD与AB的位置关系.
22.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ;
(2)函数的图象可由的图象向 _________ 平移 _________ 个单位得到;的图象可由哪个反比例函数的图象经过怎样的变换得到;
(3)一般地,函数(ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?
23.某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为某人每天120元,并且各自推出不同的优惠方案:甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.
设老年人团的人数为x
(1)根据题意,用含x的式子填写下表:
x≤35 35<x<45 x=45 x>45
甲宾馆收费/元 120x 5280
乙宾馆收费/元 120x 120x 5400
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?
答案解析部分
1.【答案】A
【解析】【解答】解:∵一次函数 的图象只经过第一、三象限,
.
故选A.
2.【答案】D
【解析】【解答】解:令y=0,则ax﹣6=0,
解得x= ,
bx﹣2=0,
解得x= ,
∵两函数在x轴上相交于同一点,
∴ = ,
整理得 = .
故选D.
【分析】分别令y=0求出与x轴的交点,再根据交点为同一点列出方程整理即可得解.
3.【答案】C
【解析】【解答】根据直角坐标系中坐标的性质,可得出A点到y轴的距离为2
故答案为:C
【分析】根据直角坐标系中坐标与距离的关系,可得出A点到y轴的距离。
4.【答案】A
【解析】【解答】解:∵反比例函数y= 与正比例函数y=kx(k<0)的图象相交于A、B两点,
∴AO=BO,
∵AC垂直x轴于C,
∴△AOC的面积= ×|﹣3|= ,
∴△BOC的面积= ,
∴△ABC的面积为3,
故选:A.
【分析】根据对称性即可得到AO=BO,再根据反比例函数系数k的几何意义,即可得到△AOC的面积,进而得到△ABC的面积为3.
5.【答案】B
【解析】【解答】解:由y=(x﹣1)0中,得
x﹣1≠0.
解得x≠1,
自变量x的取值范围是x≠1,
故选:B.
【分析】根据零指数幂的底数不能为零,可得答案.
6.【答案】C
【解析】【解答】解:A. 东经,北纬,能确定点的位置,故不符合题意;
B. 礼堂6排22号,能确定点的位置,故不符合题意;
C. 地下车库负二层,不能确定点的位置,故符合题意;
D. 港口南偏东方向上距港口10海里,能确定点的位置,故不符合题意.
故答案为:C
【分析】利用表示地理位置的方法和要求求解即可。
7.【答案】A
【解析】【分析】自变量x的取值范围是-1≤x≤3时,函数值y的取值范围是1≤y≤3,根据条件就可以得到直线经过点(-1,1)和(3,3)或(-1,3)和(3,1),根据待定系数法就可以求出函数解析式
解析:【解答】当y随x的增大而增大时,由题意得:
-k+b=1①
3k+b=3 ②
联立解得k=,b=.
故这个一次函数解析式为y=x+
当y随x的增大而减小时,
得:-k+b=3③
3k+b=1 ④
联立解得:k=-,b=.
故这个一次函数解析式为y=-x+
故选A.
【点评】本题主要考查了待定系数法求函数解析式,能够想到分两种情况讨论是解决本题的关键
8.【答案】B
【解析】【解答】当0<x≤1时,y=x2,
当1<x≤2时,ED交AB于M,EF交AB于N,如图,
CD=x,则AD=2-x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2-x,
∴EM=x-(2-x)=2x-2,
∴S△ENM= (2x-2)2=2(x-1)2,
∴y=x2-2(x-1)2=-x2+4x-2=-(x-2)2+2,
∴y= .
故答案为:B.
【分析】分类讨论:当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2-2(x-1)2,配方得到y=-(x-2)2+2,然后根据二次函数的性质对各选项进行判断.
9.【答案】C
【解析】【解答】解:∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6, ),N( ,6),
∴BN=6﹣ ,BM=6﹣ ,
∵△OMN的面积为10,
∴6×6﹣ ×6× ﹣ 6× ﹣ ×(6﹣ )2=10,
∴k=24,
∴M(6,4),N(4,6),
作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,
∵AM=AM′=4,
∴BM′=10,BN=2,
∴NM′= = =2 ,
故选C.
【分析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6, ),N( ,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
10.【答案】D
【解析】【解答】解:∵食堂在小明家和图书馆之间,小明先从家出发去食堂吃早餐,第一次路程不变处是食堂,
小明家与食堂相距0.6km,小明从家去食堂用时8min符合题意,
故①符合题意;
第二次路程不变处为图书馆,
食堂与图书馆相距=0.8-0.6=0.2 km;
故②符合题意;
从图书馆回家路程为0.8km,所用时间为68-58=10min,
∴小明从图书馆回家的速度是0.8÷10=0.08km/min,
故③符合题意;
故答案为:D.
【分析】根据图像可以看出食堂与家的距离,食堂与图书馆之间的距离。从图书馆回家的速度根据路程除以时间所得到。
11.【答案】 (答案不唯一)
【解析】【解答】解:∵反比例函数的图象在每个象限内,y的值随x值的增大而增大,
,
∴k可以取-1,
此时函数的解析式为 ,
故答案为: (答案不唯一).
【分析】当,反比例函数的图象在每个象限内,y的值随x值的增大而增大,据此解答即可(答案不唯一).
12.【答案】3
【解析】【解答】∵在平面直角坐标系中,点到y轴的距离等于其横坐标的绝对值,
∴点( ,1)到y轴的距离等于3,
故答案为:3.
【分析】在平面直角坐标系中,点到y轴的距离等于其横坐标的绝对值,据此即可得出答案.
13.【答案】y=
【解析】【解答】解:∵DE∥BC,
∴=,则=,
∴xy=2,
那么y=.
故本题答案为:y=.
【分析】根据平行线分线段成比例得到=,把DB=2,AE=1,AD=x,EC=y代入即可.
14.【答案】(﹣5,﹣3)
【解析】【解答】解:∵到x轴的距离为3,到y轴的距离为5,
∴纵坐标的绝对值为3,横坐标的绝对值为5,
∵点P在第三象限,
∴点P的坐标为(﹣5,﹣3).
故答案为(﹣5,﹣3).
【分析】根据到x轴的距离得到点P的纵坐标的绝对值,到y轴的距离得到横坐标的绝对值,进而根据所在象限判断出具体坐标即可.
15.【答案】78
【解析】【解答】解:由纵坐标看出甲先行驶了1千米,由横坐标看出甲行驶1千米用了6分钟,
甲的速度是1÷6= 千米/分钟,
由纵坐标看出AB两地的距离是16千米,
设乙的速度是x千米/分钟,由题意,得
10x+16× =16,
解得x= 千米/分钟,
相遇后乙到达A站还需(16× )÷ =2分钟,
相遇后甲到达B站还需(10× )÷ =80分钟,
当乙到达终点A时,甲还需80﹣2=78分钟到达终点B,
故答案为:78.
【分析】根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达A站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达B站需要的时间,再根据有理数的减法,可得答案.
16.【答案】解:设一次函数的解析式为y=kx+b,
将点A、B的坐标代入,得
解得:
∴一次函数的解析式为y=-3x+13
【解析】【分析】设一次函数的解析式为y=kx+b,然后将点A、B的坐标代入即可求出结论.
17.【答案】解:∵y与3x+1成正比例,
∴关系式设为:y=k(3x+1),
∵x=3时,y=4,
∴4=k(3×3+1),
解得:k= ,
∴y与x的函数关系式为:y= (3x+1)= x+ .
故y与x之间的函数关系式为:y= x+ .
【解析】【分析】首先根据题意设出关系式:y=k(3x+1),再利用待定系数法把x=3时,y=4代入,可得到k的值,再把k的值代入所设的关系式中,可得到答案.
18.【答案】解:(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
【解析】【分析】
(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;
(2)先根据图中数据把每小时用油量求出来,即:(36-6)÷3=10L,再写出函数关系式;
(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.
19.【答案】解:(1)∵反比例函数y=的图象经过点A(,1),
∴,得k=,
即k的值是;
(2)∵B(2,0)
∴OB=2
又∵△AOB绕点O逆时针旋转60°得到△COD
∴OD=OB=2,∠BOD=60°,
如右图所示,过点D作DE⊥x轴于点E,
在Rt△DOE中,
OE=OD cos60°=,DE=OD sin60°=,
∴D点坐标是(1,),
由(1)知,反比例函数的解析式,
当x=1时,y=,
∴点D(1,)在该反比例函的图象上.
【解析】【分析】(1)根据反比例函数y=的图象经过点A(,1),可以求得k的值;
(2)根据题目中信息可以画出旋转后的图形,然后求出点D的坐标,即可判断点D是否在该函数的图象上,本题得以解决.
20.【答案】解:将 代入 得
解方程组 得 或
得 的坐标为
【解析】【分析】把点 代入直线 ,求出k的值,再把两个解析式联立方程组求解即可.
21.【答案】(1)解:Ⅰ.把A点的坐标代入解析式中得:4= ,m=4,∴反比例函数的表达式为:
Ⅱ.连接AD、BC,
将b=1代入函数表达式得:a=4,又∵AC⊥x,BD⊥y,∴AC⊥BD,C(1,0),D(0,1),E(1,1),
∴CE=DE=1,AE=BE=3,
又∵ ,
∴ 且AC=BD=4,BE=AE=3,
∴ ,
∴CD∥AB;
(2)解:Ⅰ.把A点的坐标代入解析式中得:4= ,m=4,∴反比例函数的表达式为:
Ⅱ.CD∥AB,证明如下:连接AD、BC,延长BD,AC相交于点M,
由题意得M点坐标为(1,b),BM=1-a,AM=4-b,且 ,
∴ = ×4(1-a)=2(1-a),
= (-a)(4-b)= (-a)(4- )=2(1-a),
∴ ,
∴CD∥AB.
【解析】【分析】先根据问题探究的模型证明出:如果△ABC与△BCD的面积相等,那么AD∥BC。先将A点的坐标代入,根据待定系数法求出反比例函数解析式。(A)A、B两点在反比例函数同一支上,分别求出△ABC与△ADB的面积,根据算出的面积相等可类比证明CD∥AB;(B)A、B两点在反比例函数两支上,同理,分别求出△ABC与△ADB的面积,根据算出的面积相等可证明CD∥AB。
22.【答案】(1)可设新反比例函数的解析式为y=,可从原反比例函数找一点(1,1),向右平移1个单位得(2,1),代入解析式可得:a=﹣1.故所得图 象的函数表达式为;再向上平移1个单位,所得图象的函数表达式为.
(2)先把函数化为标准反比例的形式y=+1,然后即可根据反比例函数图象平移的性质解答:y=可转化为.故函数y=的图象可由的图象向上移1个单位得到;的图象可由反比例函数的图象先向右平移2个单位,再向上平移1个单位得到.
(3)函数(ab≠0,且a≠b)可转化为.
当a>0时,的图象可由反比例函数的图象向左平移a个单位,再向上平移1个单位得到;
当a<0时,的图象可由反比例函数的图象向右平移﹣a个单位,再向上平移1个单位得到.
【解析】【分析】此题可根据函数的平移变换定义,若函数图象向左平移m个单位,则x'=x+m;若函数图象向上平移n个单位,则y'=y+n;然后再把x、y代入原函数即可求解.本题考查了反比例函数平移变换的定义,题目较难,同学们要好好熟练掌握这一性质.
23.【答案】108x+420,108x+420,96x+1080解:当x≤35时,旅行团在甲、乙两家宾馆的实际花费相同,当35<x≤45时,选择甲宾馆便宜,当x>45时,甲宾馆的收费是:y甲=35×120+0.9×120(x﹣35),即y甲=108x+420,乙宾馆的收费是:y乙=45×120+0.8×120(x﹣45)=96x+1080,当y甲=y乙时,108x+420=96x+1080,解得x=55.∴当x>35时,y甲是关于人数x的一次函数,当x>45时,y乙是关于人数x的一次函数,且y甲、y乙都随人数x的增大而增大;又35<x≤45时,甲宾馆花费<乙宾馆花费,综上所述,当x>55时,有y甲>y乙总之,当x≤35或x=55时,旅行团在甲、乙两家宾馆的实际花费相同.如果老年人团的人数超过60人,在乙家宾馆住宿比较省钱
(1)108x+420;108x+420;96x+1080
(2)解:当x≤35时,旅行团在甲、乙两家宾馆的实际花费相同,
当35<x≤45时,选择甲宾馆便宜,
当x>45时,
甲宾馆的收费是:y甲=35×120+0.9×120(x﹣35),
即y甲=108x+420,
乙宾馆的收费是:y乙=45×120+0.8×120(x﹣45)=96x+1080,
当y甲=y乙时,108x+420=96x+1080,
解得x=55.
∴当x>35时,y甲是关于人数x的一次函数,
当x>45时,y乙是关于人数x的一次函数,且y甲、y乙都随人数x的增大而增大;
又35<x≤45时,甲宾馆花费<乙宾馆花费,
综上所述,当x>55时,有y甲>y乙
当x≤35或x=55时,旅行团在甲、乙两家宾馆的实际花费相同.如果老年人团的人数超过60人,在乙家宾馆住宿比较省钱
【解析】【解答】解:(1)108x+420,108x+420,96x+1080;
故答案为:108x+420,108x+420,96x+1080;
【分析】(1)由题意得,当35<x<45,y甲=35×120+0.9×120(x﹣35),即y甲=108x+420,当x>45时即y甲=108x+420,y乙=45×120+0.8×120(x﹣45)=96x+1080,(2)可分类讨论,综合两个宾馆的标准,可分为当x≤35;35<x≤45;x>45,在三个范围内讨论其是否相等.
一、单选题
1.一次函数 的图象只经过第一、三象限,则( )
A.k>0 B.k<0 C.b>0 D.b<0
2.已知一次函数y=ax﹣6与y=bx﹣2的图象在x轴上相交于同一点,则 的值是( )
A.4 B.﹣3 C.﹣ D.
3.如图,点A(-2,1)到y轴的距离为( )
A.-2 B.1 C.2 D.
4.如图,已知反比例函数y= 与正比例函数y=kx(k<0)的图象相交于A、B两点,AC垂直x轴于C,则△ABC的面积为( )
A.3 B.2 C.k D.k2
5.函数y=(x﹣1)0中,自变量x的取值范围是( )
A.x>1 B.x≠1 C.x<1 D.x≥1
6.下列不能确定点的位置的是( )
A.东经,北纬
B.礼堂6排22号
C.地下车库负二层
D.港口南偏东方向上距港口10海里
7.如果一次函数y=kx+b中自变量x的取值范围是-1≤x≤3时,函数值y的取值范围是1≤y≤3,这个一次函数解析式是()
A.y=x+或y=-x+ B.y=x+
C.y=-x+ D.y=x-
8.如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC,BC边上,C,D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
A. B.
C. D.
9.如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A.6 B.10 C.2 D.2
10.小明家、食堂、图书馆在同一条直线上,且食堂在小明家和图书馆之间.小明先从家出发去食堂吃早餐,接着去图书馆看报,然后回家,所示图象反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系.由此给出下列说法:
①小明家与食堂相距0.6km,小明从家去食堂用时8min.②食堂与图书馆相距0.2km.③小明从图书馆回家的速度是0.08 km/min.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
11.写出一个反比例函数y= (k≠0),使它的图象在每个象限内,y的值随x值的增大而增大,这个函数的解析式为 .
12.在平面直角坐标系中,点(-3,1)到 y 轴的距离等于 .
13.如图,DE∥BC,DB=2,AE=1,AD=x,EC=y,则y与x之间的函数关系为
14.已知点P在第三象限,到x轴的距离为3,到y轴的距离为5,则点P的坐标为 .
15.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.
三、解答题
16.一次函数的图象经过A(3,4)和点B(2,7),求此一次函数的表达式.
17.已知y与3x+1成正比例,且x=3时,y=4.求y与x之间的函数关系式.
18.小丽一家利用元旦三天驾车到某景点旅游。小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
19.在平面直角坐标系中,已知A(,1),B(2,0),O(0,0),反比例函数y=的图象经过点A.
(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,点B与点D对应,试判断点D是否在该反比例函数的图象上.
20.直线 与反比例函数 (其中 )的图象交于 、 ,求点 的坐标.
21.说明:在解答“结论应用”时,从A,B两题中任选一题作答.
问题探究:
启知学习小组在课外学习时,发现了这样一个问题:如图①,在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图①中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
结论应用:
在平面直角坐标系中,反比例函数y= (x≠0)的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(1)A
Ⅰ.求反比例函数的表达式;
Ⅱ.如图②,已知b=1,AC,BD相交于点E,求证:CD∥AB.
(2)B
Ⅰ.求反比例函数的表达式;
Ⅱ.如图③,若点B在第三象限,判断并证明CD与AB的位置关系.
22.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ;
(2)函数的图象可由的图象向 _________ 平移 _________ 个单位得到;的图象可由哪个反比例函数的图象经过怎样的变换得到;
(3)一般地,函数(ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?
23.某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为某人每天120元,并且各自推出不同的优惠方案:甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.
设老年人团的人数为x
(1)根据题意,用含x的式子填写下表:
x≤35 35<x<45 x=45 x>45
甲宾馆收费/元 120x 5280
乙宾馆收费/元 120x 120x 5400
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?
答案解析部分
1.【答案】A
【解析】【解答】解:∵一次函数 的图象只经过第一、三象限,
.
故选A.
2.【答案】D
【解析】【解答】解:令y=0,则ax﹣6=0,
解得x= ,
bx﹣2=0,
解得x= ,
∵两函数在x轴上相交于同一点,
∴ = ,
整理得 = .
故选D.
【分析】分别令y=0求出与x轴的交点,再根据交点为同一点列出方程整理即可得解.
3.【答案】C
【解析】【解答】根据直角坐标系中坐标的性质,可得出A点到y轴的距离为2
故答案为:C
【分析】根据直角坐标系中坐标与距离的关系,可得出A点到y轴的距离。
4.【答案】A
【解析】【解答】解:∵反比例函数y= 与正比例函数y=kx(k<0)的图象相交于A、B两点,
∴AO=BO,
∵AC垂直x轴于C,
∴△AOC的面积= ×|﹣3|= ,
∴△BOC的面积= ,
∴△ABC的面积为3,
故选:A.
【分析】根据对称性即可得到AO=BO,再根据反比例函数系数k的几何意义,即可得到△AOC的面积,进而得到△ABC的面积为3.
5.【答案】B
【解析】【解答】解:由y=(x﹣1)0中,得
x﹣1≠0.
解得x≠1,
自变量x的取值范围是x≠1,
故选:B.
【分析】根据零指数幂的底数不能为零,可得答案.
6.【答案】C
【解析】【解答】解:A. 东经,北纬,能确定点的位置,故不符合题意;
B. 礼堂6排22号,能确定点的位置,故不符合题意;
C. 地下车库负二层,不能确定点的位置,故符合题意;
D. 港口南偏东方向上距港口10海里,能确定点的位置,故不符合题意.
故答案为:C
【分析】利用表示地理位置的方法和要求求解即可。
7.【答案】A
【解析】【分析】自变量x的取值范围是-1≤x≤3时,函数值y的取值范围是1≤y≤3,根据条件就可以得到直线经过点(-1,1)和(3,3)或(-1,3)和(3,1),根据待定系数法就可以求出函数解析式
解析:【解答】当y随x的增大而增大时,由题意得:
-k+b=1①
3k+b=3 ②
联立解得k=,b=.
故这个一次函数解析式为y=x+
当y随x的增大而减小时,
得:-k+b=3③
3k+b=1 ④
联立解得:k=-,b=.
故这个一次函数解析式为y=-x+
故选A.
【点评】本题主要考查了待定系数法求函数解析式,能够想到分两种情况讨论是解决本题的关键
8.【答案】B
【解析】【解答】当0<x≤1时,y=x2,
当1<x≤2时,ED交AB于M,EF交AB于N,如图,
CD=x,则AD=2-x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2-x,
∴EM=x-(2-x)=2x-2,
∴S△ENM= (2x-2)2=2(x-1)2,
∴y=x2-2(x-1)2=-x2+4x-2=-(x-2)2+2,
∴y= .
故答案为:B.
【分析】分类讨论:当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2-2(x-1)2,配方得到y=-(x-2)2+2,然后根据二次函数的性质对各选项进行判断.
9.【答案】C
【解析】【解答】解:∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6, ),N( ,6),
∴BN=6﹣ ,BM=6﹣ ,
∵△OMN的面积为10,
∴6×6﹣ ×6× ﹣ 6× ﹣ ×(6﹣ )2=10,
∴k=24,
∴M(6,4),N(4,6),
作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,
∵AM=AM′=4,
∴BM′=10,BN=2,
∴NM′= = =2 ,
故选C.
【分析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6, ),N( ,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
10.【答案】D
【解析】【解答】解:∵食堂在小明家和图书馆之间,小明先从家出发去食堂吃早餐,第一次路程不变处是食堂,
小明家与食堂相距0.6km,小明从家去食堂用时8min符合题意,
故①符合题意;
第二次路程不变处为图书馆,
食堂与图书馆相距=0.8-0.6=0.2 km;
故②符合题意;
从图书馆回家路程为0.8km,所用时间为68-58=10min,
∴小明从图书馆回家的速度是0.8÷10=0.08km/min,
故③符合题意;
故答案为:D.
【分析】根据图像可以看出食堂与家的距离,食堂与图书馆之间的距离。从图书馆回家的速度根据路程除以时间所得到。
11.【答案】 (答案不唯一)
【解析】【解答】解:∵反比例函数的图象在每个象限内,y的值随x值的增大而增大,
,
∴k可以取-1,
此时函数的解析式为 ,
故答案为: (答案不唯一).
【分析】当,反比例函数的图象在每个象限内,y的值随x值的增大而增大,据此解答即可(答案不唯一).
12.【答案】3
【解析】【解答】∵在平面直角坐标系中,点到y轴的距离等于其横坐标的绝对值,
∴点( ,1)到y轴的距离等于3,
故答案为:3.
【分析】在平面直角坐标系中,点到y轴的距离等于其横坐标的绝对值,据此即可得出答案.
13.【答案】y=
【解析】【解答】解:∵DE∥BC,
∴=,则=,
∴xy=2,
那么y=.
故本题答案为:y=.
【分析】根据平行线分线段成比例得到=,把DB=2,AE=1,AD=x,EC=y代入即可.
14.【答案】(﹣5,﹣3)
【解析】【解答】解:∵到x轴的距离为3,到y轴的距离为5,
∴纵坐标的绝对值为3,横坐标的绝对值为5,
∵点P在第三象限,
∴点P的坐标为(﹣5,﹣3).
故答案为(﹣5,﹣3).
【分析】根据到x轴的距离得到点P的纵坐标的绝对值,到y轴的距离得到横坐标的绝对值,进而根据所在象限判断出具体坐标即可.
15.【答案】78
【解析】【解答】解:由纵坐标看出甲先行驶了1千米,由横坐标看出甲行驶1千米用了6分钟,
甲的速度是1÷6= 千米/分钟,
由纵坐标看出AB两地的距离是16千米,
设乙的速度是x千米/分钟,由题意,得
10x+16× =16,
解得x= 千米/分钟,
相遇后乙到达A站还需(16× )÷ =2分钟,
相遇后甲到达B站还需(10× )÷ =80分钟,
当乙到达终点A时,甲还需80﹣2=78分钟到达终点B,
故答案为:78.
【分析】根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达A站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达B站需要的时间,再根据有理数的减法,可得答案.
16.【答案】解:设一次函数的解析式为y=kx+b,
将点A、B的坐标代入,得
解得:
∴一次函数的解析式为y=-3x+13
【解析】【分析】设一次函数的解析式为y=kx+b,然后将点A、B的坐标代入即可求出结论.
17.【答案】解:∵y与3x+1成正比例,
∴关系式设为:y=k(3x+1),
∵x=3时,y=4,
∴4=k(3×3+1),
解得:k= ,
∴y与x的函数关系式为:y= (3x+1)= x+ .
故y与x之间的函数关系式为:y= x+ .
【解析】【分析】首先根据题意设出关系式:y=k(3x+1),再利用待定系数法把x=3时,y=4代入,可得到k的值,再把k的值代入所设的关系式中,可得到答案.
18.【答案】解:(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
【解析】【分析】
(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;
(2)先根据图中数据把每小时用油量求出来,即:(36-6)÷3=10L,再写出函数关系式;
(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.
19.【答案】解:(1)∵反比例函数y=的图象经过点A(,1),
∴,得k=,
即k的值是;
(2)∵B(2,0)
∴OB=2
又∵△AOB绕点O逆时针旋转60°得到△COD
∴OD=OB=2,∠BOD=60°,
如右图所示,过点D作DE⊥x轴于点E,
在Rt△DOE中,
OE=OD cos60°=,DE=OD sin60°=,
∴D点坐标是(1,),
由(1)知,反比例函数的解析式,
当x=1时,y=,
∴点D(1,)在该反比例函的图象上.
【解析】【分析】(1)根据反比例函数y=的图象经过点A(,1),可以求得k的值;
(2)根据题目中信息可以画出旋转后的图形,然后求出点D的坐标,即可判断点D是否在该函数的图象上,本题得以解决.
20.【答案】解:将 代入 得
解方程组 得 或
得 的坐标为
【解析】【分析】把点 代入直线 ,求出k的值,再把两个解析式联立方程组求解即可.
21.【答案】(1)解:Ⅰ.把A点的坐标代入解析式中得:4= ,m=4,∴反比例函数的表达式为:
Ⅱ.连接AD、BC,
将b=1代入函数表达式得:a=4,又∵AC⊥x,BD⊥y,∴AC⊥BD,C(1,0),D(0,1),E(1,1),
∴CE=DE=1,AE=BE=3,
又∵ ,
∴ 且AC=BD=4,BE=AE=3,
∴ ,
∴CD∥AB;
(2)解:Ⅰ.把A点的坐标代入解析式中得:4= ,m=4,∴反比例函数的表达式为:
Ⅱ.CD∥AB,证明如下:连接AD、BC,延长BD,AC相交于点M,
由题意得M点坐标为(1,b),BM=1-a,AM=4-b,且 ,
∴ = ×4(1-a)=2(1-a),
= (-a)(4-b)= (-a)(4- )=2(1-a),
∴ ,
∴CD∥AB.
【解析】【分析】先根据问题探究的模型证明出:如果△ABC与△BCD的面积相等,那么AD∥BC。先将A点的坐标代入,根据待定系数法求出反比例函数解析式。(A)A、B两点在反比例函数同一支上,分别求出△ABC与△ADB的面积,根据算出的面积相等可类比证明CD∥AB;(B)A、B两点在反比例函数两支上,同理,分别求出△ABC与△ADB的面积,根据算出的面积相等可证明CD∥AB。
22.【答案】(1)可设新反比例函数的解析式为y=,可从原反比例函数找一点(1,1),向右平移1个单位得(2,1),代入解析式可得:a=﹣1.故所得图 象的函数表达式为;再向上平移1个单位,所得图象的函数表达式为.
(2)先把函数化为标准反比例的形式y=+1,然后即可根据反比例函数图象平移的性质解答:y=可转化为.故函数y=的图象可由的图象向上移1个单位得到;的图象可由反比例函数的图象先向右平移2个单位,再向上平移1个单位得到.
(3)函数(ab≠0,且a≠b)可转化为.
当a>0时,的图象可由反比例函数的图象向左平移a个单位,再向上平移1个单位得到;
当a<0时,的图象可由反比例函数的图象向右平移﹣a个单位,再向上平移1个单位得到.
【解析】【分析】此题可根据函数的平移变换定义,若函数图象向左平移m个单位,则x'=x+m;若函数图象向上平移n个单位,则y'=y+n;然后再把x、y代入原函数即可求解.本题考查了反比例函数平移变换的定义,题目较难,同学们要好好熟练掌握这一性质.
23.【答案】108x+420,108x+420,96x+1080解:当x≤35时,旅行团在甲、乙两家宾馆的实际花费相同,当35<x≤45时,选择甲宾馆便宜,当x>45时,甲宾馆的收费是:y甲=35×120+0.9×120(x﹣35),即y甲=108x+420,乙宾馆的收费是:y乙=45×120+0.8×120(x﹣45)=96x+1080,当y甲=y乙时,108x+420=96x+1080,解得x=55.∴当x>35时,y甲是关于人数x的一次函数,当x>45时,y乙是关于人数x的一次函数,且y甲、y乙都随人数x的增大而增大;又35<x≤45时,甲宾馆花费<乙宾馆花费,综上所述,当x>55时,有y甲>y乙总之,当x≤35或x=55时,旅行团在甲、乙两家宾馆的实际花费相同.如果老年人团的人数超过60人,在乙家宾馆住宿比较省钱
(1)108x+420;108x+420;96x+1080
(2)解:当x≤35时,旅行团在甲、乙两家宾馆的实际花费相同,
当35<x≤45时,选择甲宾馆便宜,
当x>45时,
甲宾馆的收费是:y甲=35×120+0.9×120(x﹣35),
即y甲=108x+420,
乙宾馆的收费是:y乙=45×120+0.8×120(x﹣45)=96x+1080,
当y甲=y乙时,108x+420=96x+1080,
解得x=55.
∴当x>35时,y甲是关于人数x的一次函数,
当x>45时,y乙是关于人数x的一次函数,且y甲、y乙都随人数x的增大而增大;
又35<x≤45时,甲宾馆花费<乙宾馆花费,
综上所述,当x>55时,有y甲>y乙
当x≤35或x=55时,旅行团在甲、乙两家宾馆的实际花费相同.如果老年人团的人数超过60人,在乙家宾馆住宿比较省钱
【解析】【解答】解:(1)108x+420,108x+420,96x+1080;
故答案为:108x+420,108x+420,96x+1080;
【分析】(1)由题意得,当35<x<45,y甲=35×120+0.9×120(x﹣35),即y甲=108x+420,当x>45时即y甲=108x+420,y乙=45×120+0.8×120(x﹣45)=96x+1080,(2)可分类讨论,综合两个宾馆的标准,可分为当x≤35;35<x≤45;x>45,在三个范围内讨论其是否相等.
