苏科版八年级上第5章一次函数复习(无答案)[上学期]
文档属性
| 名称 | 苏科版八年级上第5章一次函数复习(无答案)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 25.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-25 20:15:00 | ||
图片预览

文档简介
本章知识框架
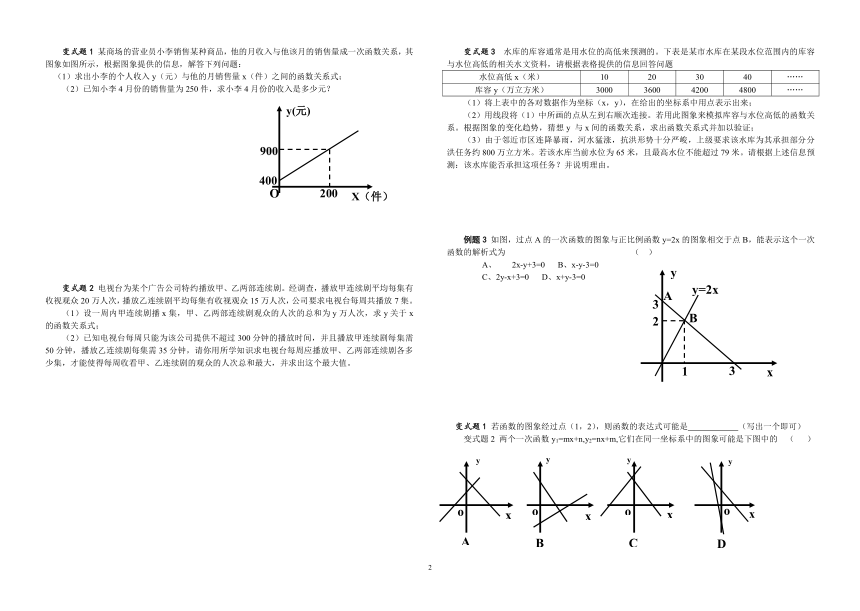
例题1 某污水处理厂的一个净化池设有2个进水口和1个出水口,三个水口至少打开一个,每个进水口进水速度由图甲给出,出水口出水的速度由图乙给出。某一天0点到6点,该水池的蓄水量与时间的函数关系如图丙所示。通过对图象的观察,小亮得出了以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水;(3)4点到6点不进水也不出水。其中正确的是 ( )
A、(1) B、(1)(2) C、(1)(3) D、(1)(2)(3)
变式题 一列火车从扬州站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达火车站减速停下,图中大致刻画火车在这段时间内速度随时间变化情况的是 ( )
例题2 某出版社出版一种适合中学生阅读的科普读物,若该读物首次印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册) 5000 8000 10000 15000 ……
成本y(元) 28500 36000 41000 53500 ……
(1)经过对上表数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入48000元,那么能印读物多少册?
变式题1 某商场的营业员小李销售某种商品,他的月收入与他该月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:
(1)求出小李的个人收入y(元)与他的月销售量x(件)之间的函数关系式;
(2)已知小李4月份的销售量为250件,求小李4月份的收入是多少元?
变式题2 电视台为某个广告公司特约播放甲、乙两部连续剧。经调查,播放甲连续剧平均每集有收视观众20万人次,播放乙连续剧平均每集有收视观众15万人次,公司要求电视台每周共播放7集。
(1)设一周内甲连续剧播x集,甲、乙两部连续剧观众的人次的总和为y万人次,求y关于x的函数关系式;
(2)已知电视台每周只能为该公司提供不超过300分钟的播放时间,并且播放甲连续剧每集需50分钟,播放乙连续剧每集需35分钟,请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集,才能使得每周收看甲、乙连续剧的观众的人次总和最大,并求出这个最大值。
变式题3 水库的库容通常是用水位的高低来预测的。下表是某市水库在某段水位范围内的库容与水位高低的相关水文资料,请根据表格提供的信息回答问题
水位高低x(米) 10 20 30 40 ……
库容y(万立方米) 3000 3600 4200 4800 ……
(1)将上表中的各对数据作为坐标(x,y),在给出的坐标系中用点表示出来;
(2)用线段将(1)中所画的点从左到右顺次连接。若用此图象来模拟库容与水位高低的函数关系。根据图象的变化趋势,猜想y 与x间的函数关系,求出函数关系式并加以验证;
(3)由于邻近市区连降暴雨,河水猛涨,抗洪形势十分严峻,上级要求该水库为其承担部分分洪任务约800万立方米。若该水库当前水位为65米,且最高水位不能超过79米。请根据上述信息预测:该水库能否承担这项任务?并说明理由。
例题3 如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,能表示这个一次函数的解析式为 ( )
A、 2x-y+3=0 B、x-y-3=0
C、2y-x+3=0 D、x+y-3=0
变式题1 若函数的图象经过点(1,2),则函数的表达式可能是 (写出一个即可)
变式题2 两个一次函数y1=mx+n,y2=nx+m,它们在同一坐标系中的图象可能是下图中的 ( )
变式题3 在函数y=-2x+3中,当自变量x满足 时,图象在第一象限。
例题4 如图,表示甲骑电动自行车和乙驾驶汽车均行驶90km的过程中,行驶的路程与经过的时间的函数关系,请根据图象填空: 出发早,早了
小时, 先到达,先到 小时,电动自行车的速度为 km/h,汽车的速度为 km/h。
变式题1 学校准备周末组织老师去南京参加艺术节,现有甲、乙两家旅行社表示对老师优惠。设参加艺术节的老师有x人, 甲、乙两家旅行社实际收费y甲、y乙与x的函数关系如图所示,根据图象信息,请你回答下列问题:
(1)当x满足 时,两家旅行社的收费相同;
(2)当x满足 时,选择甲旅行社合适。
变式题2 某企业有甲、乙两个长方形的蓄水池,将甲池中的水以每小时立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图所示,结合图象回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池蓄水量深度同;
中考名题欣赏
1、已知一次函数y=kx+b的图象经过点(0,1)且不经过第四象限,则满足以上条件的一个一次函数的解析式为
2、下面是用棋子摆成的“上”字:如果按照以下的规律摆下去,那么通过观察发现:第n个“上”需用
枚棋子,棋子数s与n之间的函数关系式为
3、下图是用火柴棒摆成边长分别是1、2、3根时的正方形,当边长为n根火柴棒时,若摆出的正方形所用火柴棒的根数为s时,则s= (用含n的代数式表示,n为正整数)。
4、若正比例函数y=kx与 y=2x的图象关于x轴对称,则k的值等于
5、如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是 ( )
6、如图所示,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h与注水时间t之间的函数关系,大致是下
列图象中的 ( )
7、一次函数y=kx+b满足kb>0且y随x的增大而减小则,此函数图象不经过 ( )
A、第1象限 B、第2象限 C、第3象限 D、第4象限
8、某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,下图表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1、y2的解析式;
(2)解释图中表示的两重方案是如何付推销费的;
(3)如果你是推销员,应如何选择付费方案?
9、某摩托车的油箱最多可存油5升,行驶时油箱内余油量y(升)与行驶路程x(km)成一次函数关系,其图象如图所示
(1)求y 与x的函数关系式;
(2)摩托车加满油后到完全燃烧,最多能行驶多少km?
10、当a、b满足何值时,函数y=(2a-1)x3-b+(a+b)
(1)是一次函数?(2)使正比例函数?
11、已知正比例函数y=k1x的图象与一次函数y= k1x-9的图象相交于点P(3,-6)。
(1)求k1、k2的值;
(2)如果一次函数y= k1x-9的图象与x轴交于点A,求A的坐标。
12、某加工厂已每吨3000元的价格购进50吨原料进行加工,若进行粗加工,每吨加工费用为600元,需天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需天,每吨售价4500元。现将这50吨原料全部加工完。(1)设其中粗加工x吨,获利y元,求y与x之间的函数关系式(不要求写自变量的范围);(2)如果必须在20天内完成,如何安排生产才能获得最大利润?最大利润是多少?
13、甲骑自行车、乙骑摩托车沿相同的路线由A
地到B地,行驶过程中路程与时间的函数关系的
图象如图,根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终
点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中
(不包括起点和终点)?在这一段时间内,
请你根据下列情形,分别列出关于行驶时间x
的方程或不等式(不化简,也不求解):
①甲在乙的前面;②甲与乙相遇;③甲在乙后面。
图象法
列表法
变 量
常量
自变量、因变量
函数的表示方法
一次函数
解析法
图象
图象的应用
函数表达式的确定
函数的表达式
设出含有待定系数的
解析式y=kx+b
一般步骤
待定系数法
把已知条件代入解析式得关于待定系数的方程组
在坐标系中求出交点坐标
将k、b代入解析式y=kx+b
解方程组求出待定系数k、b
该交点坐标即为原方程组的解
画表示两个方程的一次函数图象
求二元一次方程组的解
一般步骤
图甲
O
进水量(立方米)
20
2
时间(小时)
时间(小时)
时间(小时)
出水量(立方米)
进水量(立方米)
O
O
60
50
20
1
6
5
4
3
图乙
图丙
A
速度
时间
O
速度
时间
O
速度
时间
O
C
速度
时间
O
B
D
O
200
y(元)
X(件)
900
400
3
1
3
B
A
2
y=2x
y
x
x
x
x
x
y
y
y
y
o
o
o
o
A
B
C
D
o
y(km)
电动自行车
汽车
x(h)
1
2
90
5
4
3
60
40
20
x(h)
y(m)
3
1
2
4
甲
乙
y乙
y甲
o
20
x(人)
y(元)
2000
600
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
……
A
y
x
y
y
y
x
x
x
B
C
D
A
h
o
t
h
o
t
h
o
t
h
o
t
B
C
D
B
0
A
60
3
5
y(升)
x(km)
300
o
x(件)
600
30
y2
y1
y(元)
x(min)
3
y(km)
2
5
o
20
15
10
1
30
25
6
5
4
乙
甲
PAGE
1
例题1 某污水处理厂的一个净化池设有2个进水口和1个出水口,三个水口至少打开一个,每个进水口进水速度由图甲给出,出水口出水的速度由图乙给出。某一天0点到6点,该水池的蓄水量与时间的函数关系如图丙所示。通过对图象的观察,小亮得出了以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水;(3)4点到6点不进水也不出水。其中正确的是 ( )
A、(1) B、(1)(2) C、(1)(3) D、(1)(2)(3)
变式题 一列火车从扬州站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达火车站减速停下,图中大致刻画火车在这段时间内速度随时间变化情况的是 ( )
例题2 某出版社出版一种适合中学生阅读的科普读物,若该读物首次印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册) 5000 8000 10000 15000 ……
成本y(元) 28500 36000 41000 53500 ……
(1)经过对上表数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入48000元,那么能印读物多少册?
变式题1 某商场的营业员小李销售某种商品,他的月收入与他该月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:
(1)求出小李的个人收入y(元)与他的月销售量x(件)之间的函数关系式;
(2)已知小李4月份的销售量为250件,求小李4月份的收入是多少元?
变式题2 电视台为某个广告公司特约播放甲、乙两部连续剧。经调查,播放甲连续剧平均每集有收视观众20万人次,播放乙连续剧平均每集有收视观众15万人次,公司要求电视台每周共播放7集。
(1)设一周内甲连续剧播x集,甲、乙两部连续剧观众的人次的总和为y万人次,求y关于x的函数关系式;
(2)已知电视台每周只能为该公司提供不超过300分钟的播放时间,并且播放甲连续剧每集需50分钟,播放乙连续剧每集需35分钟,请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集,才能使得每周收看甲、乙连续剧的观众的人次总和最大,并求出这个最大值。
变式题3 水库的库容通常是用水位的高低来预测的。下表是某市水库在某段水位范围内的库容与水位高低的相关水文资料,请根据表格提供的信息回答问题
水位高低x(米) 10 20 30 40 ……
库容y(万立方米) 3000 3600 4200 4800 ……
(1)将上表中的各对数据作为坐标(x,y),在给出的坐标系中用点表示出来;
(2)用线段将(1)中所画的点从左到右顺次连接。若用此图象来模拟库容与水位高低的函数关系。根据图象的变化趋势,猜想y 与x间的函数关系,求出函数关系式并加以验证;
(3)由于邻近市区连降暴雨,河水猛涨,抗洪形势十分严峻,上级要求该水库为其承担部分分洪任务约800万立方米。若该水库当前水位为65米,且最高水位不能超过79米。请根据上述信息预测:该水库能否承担这项任务?并说明理由。
例题3 如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,能表示这个一次函数的解析式为 ( )
A、 2x-y+3=0 B、x-y-3=0
C、2y-x+3=0 D、x+y-3=0
变式题1 若函数的图象经过点(1,2),则函数的表达式可能是 (写出一个即可)
变式题2 两个一次函数y1=mx+n,y2=nx+m,它们在同一坐标系中的图象可能是下图中的 ( )
变式题3 在函数y=-2x+3中,当自变量x满足 时,图象在第一象限。
例题4 如图,表示甲骑电动自行车和乙驾驶汽车均行驶90km的过程中,行驶的路程与经过的时间的函数关系,请根据图象填空: 出发早,早了
小时, 先到达,先到 小时,电动自行车的速度为 km/h,汽车的速度为 km/h。
变式题1 学校准备周末组织老师去南京参加艺术节,现有甲、乙两家旅行社表示对老师优惠。设参加艺术节的老师有x人, 甲、乙两家旅行社实际收费y甲、y乙与x的函数关系如图所示,根据图象信息,请你回答下列问题:
(1)当x满足 时,两家旅行社的收费相同;
(2)当x满足 时,选择甲旅行社合适。
变式题2 某企业有甲、乙两个长方形的蓄水池,将甲池中的水以每小时立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图所示,结合图象回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池蓄水量深度同;
中考名题欣赏
1、已知一次函数y=kx+b的图象经过点(0,1)且不经过第四象限,则满足以上条件的一个一次函数的解析式为
2、下面是用棋子摆成的“上”字:如果按照以下的规律摆下去,那么通过观察发现:第n个“上”需用
枚棋子,棋子数s与n之间的函数关系式为
3、下图是用火柴棒摆成边长分别是1、2、3根时的正方形,当边长为n根火柴棒时,若摆出的正方形所用火柴棒的根数为s时,则s= (用含n的代数式表示,n为正整数)。
4、若正比例函数y=kx与 y=2x的图象关于x轴对称,则k的值等于
5、如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是 ( )
6、如图所示,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h与注水时间t之间的函数关系,大致是下
列图象中的 ( )
7、一次函数y=kx+b满足kb>0且y随x的增大而减小则,此函数图象不经过 ( )
A、第1象限 B、第2象限 C、第3象限 D、第4象限
8、某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,下图表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1、y2的解析式;
(2)解释图中表示的两重方案是如何付推销费的;
(3)如果你是推销员,应如何选择付费方案?
9、某摩托车的油箱最多可存油5升,行驶时油箱内余油量y(升)与行驶路程x(km)成一次函数关系,其图象如图所示
(1)求y 与x的函数关系式;
(2)摩托车加满油后到完全燃烧,最多能行驶多少km?
10、当a、b满足何值时,函数y=(2a-1)x3-b+(a+b)
(1)是一次函数?(2)使正比例函数?
11、已知正比例函数y=k1x的图象与一次函数y= k1x-9的图象相交于点P(3,-6)。
(1)求k1、k2的值;
(2)如果一次函数y= k1x-9的图象与x轴交于点A,求A的坐标。
12、某加工厂已每吨3000元的价格购进50吨原料进行加工,若进行粗加工,每吨加工费用为600元,需天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需天,每吨售价4500元。现将这50吨原料全部加工完。(1)设其中粗加工x吨,获利y元,求y与x之间的函数关系式(不要求写自变量的范围);(2)如果必须在20天内完成,如何安排生产才能获得最大利润?最大利润是多少?
13、甲骑自行车、乙骑摩托车沿相同的路线由A
地到B地,行驶过程中路程与时间的函数关系的
图象如图,根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终
点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中
(不包括起点和终点)?在这一段时间内,
请你根据下列情形,分别列出关于行驶时间x
的方程或不等式(不化简,也不求解):
①甲在乙的前面;②甲与乙相遇;③甲在乙后面。
图象法
列表法
变 量
常量
自变量、因变量
函数的表示方法
一次函数
解析法
图象
图象的应用
函数表达式的确定
函数的表达式
设出含有待定系数的
解析式y=kx+b
一般步骤
待定系数法
把已知条件代入解析式得关于待定系数的方程组
在坐标系中求出交点坐标
将k、b代入解析式y=kx+b
解方程组求出待定系数k、b
该交点坐标即为原方程组的解
画表示两个方程的一次函数图象
求二元一次方程组的解
一般步骤
图甲
O
进水量(立方米)
20
2
时间(小时)
时间(小时)
时间(小时)
出水量(立方米)
进水量(立方米)
O
O
60
50
20
1
6
5
4
3
图乙
图丙
A
速度
时间
O
速度
时间
O
速度
时间
O
C
速度
时间
O
B
D
O
200
y(元)
X(件)
900
400
3
1
3
B
A
2
y=2x
y
x
x
x
x
x
y
y
y
y
o
o
o
o
A
B
C
D
o
y(km)
电动自行车
汽车
x(h)
1
2
90
5
4
3
60
40
20
x(h)
y(m)
3
1
2
4
甲
乙
y乙
y甲
o
20
x(人)
y(元)
2000
600
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
……
A
y
x
y
y
y
x
x
x
B
C
D
A
h
o
t
h
o
t
h
o
t
h
o
t
B
C
D
B
0
A
60
3
5
y(升)
x(km)
300
o
x(件)
600
30
y2
y1
y(元)
x(min)
3
y(km)
2
5
o
20
15
10
1
30
25
6
5
4
乙
甲
PAGE
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
