第4单元正比例与反比例重难点检测卷(单元测试)-小学数学六年级下册北师大版(含答案)
文档属性
| 名称 | 第4单元正比例与反比例重难点检测卷(单元测试)-小学数学六年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 09:33:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4单元正比例与反比例重难点检测卷(单元测试)-小学数学六年级下册北师大版
一、选择题
1.微信朋友圈的总人数一定,朋友圈内点赞人数的数量与未点赞人数的数量( )比例。
A.成正 B.成反 C.不成 D.无法确定
2.圆锥的体积一定,它的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.一个圆的半径与它的周长( )。
A.成正比例 B.成反比例 C.不成比例 D.没有关系
4.下列变化的量中,成反比例的是( )。
A.长方形的长一定,宽和面积 B.一袋大米,吃去的数量和剩下的数量
C.4a=5b(a、b不为0),那么a和b D.平行四边形的面积不变,它的底与高
5.下面几个关系中,x和y(x、y不为0)成反比例关系的是( )。
A. B. C. D.
6.在比例尺是1∶8的图纸上,甲、乙两个圆的直径比是2∶3,那么甲、乙两个圆实际的直径比是( )。
A.1∶8 B.2∶3 C.4∶9 D.9∶4
二、填空题
7.一个圆锥有( )条高,如果高一定,它的体积与底面积成( )比例。
8.行驶的路程一定,车轮的周长与车轮需要转动的圈数成( )比例。正方体的表面积与它的一个面的面积成( )比例。
9.已知y=4x,当x=2时,y=( );当y=4.8时,x=( ),x与y成( )比例。
10.如果下表x和y成正比例,那么“?”处应填( );如果x和y成反比例,那么“?”处应填( )。
x 24 ?
y 3 4
11.因为x∶7=y∶6(x≠0,y≠0),所以x和y成( )比例。
12.慢车和快车沿相同的路线从地到地所行路程和时间的关系如图所示:
(1)慢车行驶时间和路程成( )比例关系。
(2)快车追上慢车所需时间是( )小时。
(3)、两地之间的路程是( )千米。
13.一箱荔枝,平均分给一些小朋友。
每人分的颗数 1 2 3 4 ( ) 10
可分的人数 120 60 ( ) ( ) 24 ( )
(1)完成表格。
(2)从表格中可以看出,( )不变。
(3)每人分的颗数与可分的人数成( )比例关系。
14.84消毒液是一种无色或淡黄色的液体,是一种高效消毒剂。疫情期间被广泛用于宾馆、旅游、医院、家庭、学校等的卫生消毒,消毒方法:擦拭,喷洒,拖洗消毒。常用的有1∶500和1∶200两种84消毒液配制方法。
1∶500的84消毒液配制如下:
加清水 500克 2500克 5000克
84消毒液 1毫升 5毫升 10毫升
假如现在是1∶200的84消毒液配制,请完成下表:
加清水 500克 2500克 5000克
84消毒液 _____毫升 _____毫升 _____毫升
三、判断题
15.报刊的单价一定,报刊的份数和总价成正比例。 ( )
16.每年体检,班里近视的人数和不近视的人数成反比例。 ( )
17.花生的出油率一定,油的质量和花生的质量成反比例。 ( )
18.已知5x-3y=0,那么x与y成正比例。( )
19.正比例图象是一条直线。( )
四、计算题
20.解方程。
五、解答题
21.小东从家出发去学校,如果每分走70米,能在上课前5分到校;如果每分走45米,就要迟到5分。那么小东家到学校的路程是多少米?
22.一列磁悬浮列车匀速行驶,其所用时间和行驶路程关系如下表。
(1)把下表填写完整。
时间/分 1 2 3 4 5 …
路程/千米 7.5 15 22.5 ( ) ( ) …
(2)表中两种变化的量是( )和( ),不变的量是( )。
(3)这列磁悬浮列车行驶的路程和所需时间是否成正比例或反比例?为什么?
23.一种茶叶500克售价99元,李叔叔要买2.3千克这种茶叶,应付多少元?(用比例知识解答)
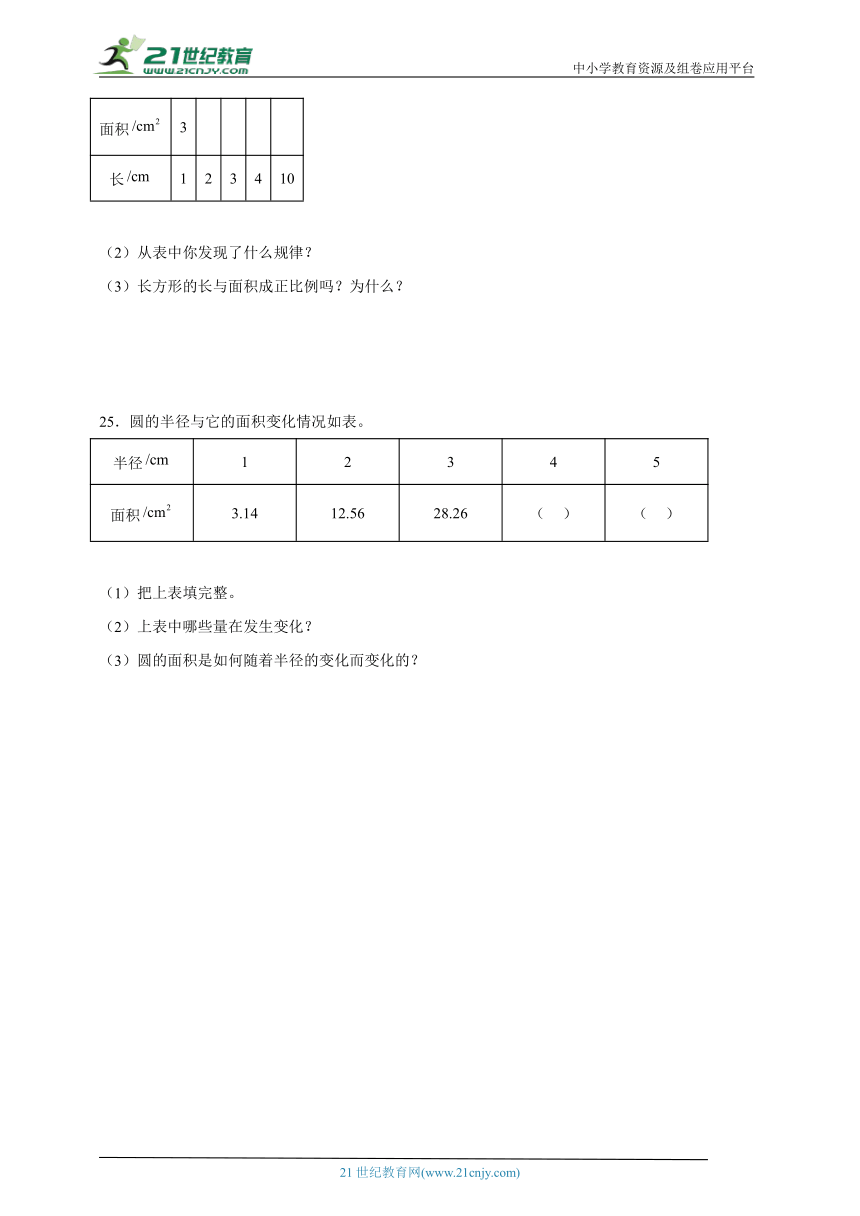
24.长方形的一条边长度是。
(1)把表填完整。
面积 3
长 1 2 3 4 10
(2)从表中你发现了什么规律?
(3)长方形的长与面积成正比例吗?为什么?
25.圆的半径与它的面积变化情况如表。
半径 1 2 3 4 5
面积 3.14 12.56 28.26 ( ) ( )
(1)把上表填完整。
(2)上表中哪些量在发生变化?
(3)圆的面积是如何随着半径的变化而变化的?
参考答案:
1.C
【分析】两个相关联的量,如果它们的比值一定,成正比例关系;如果它们的乘积一定,成反比例关系,据此解答。
【详解】点赞人数的数量+未点赞人数的数量=朋友圈的总人数(一定),和一定,不成比例。
故答案为:C
【点睛】判断两个相关联的两个量成什么比例,主要看它们是比值一定还是乘积一定。
2.B
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例。根据:圆锥的体积=底面积×高×,可知底面积与高的乘积是圆锥体积的,即是乘积一定,所以是反比例。
【详解】根据:圆锥的体积=底面积×高×,可知底面积与高的乘积是圆锥体积的;所以,圆锥的体积一定,它的底面积和高成反比例。
故答案为:B
【点睛】熟记圆锥的体积就是公式是解答此题的关键。
3.A
【分析】两个相关联的量,如果它们的比值一定,成正比例关系;如果它们的乘积一定,成反比例关系,据此解答。
【详解】 =2π,因为2π是定值,也就是周长与半径的比值一定,所以成正比例关系。
故选择:A
【点睛】此题考查了正、反比例的辨别,主要看两个量是比值一定还是乘积一定。
4.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.长方形的长一定,宽和面积比值一定,成正比例;
B.一袋大米,吃去的数量和剩下的数量,不成比例;
C.4a=5b(a、b不为0),那么a和b比值一定,成正比例;
D.平行四边形的面积不变,它的底与高乘积一定,成反比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5.B
【分析】判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。
【详解】A.因为:(一定),所以x和y成正比例,不合题意;
B.由比例的基本性质可知:x×y=10(一定),所以x和y成反比例,符合题意;
C.(一定),这是和一定,所以x和y不成比例;
D.由,得,即,所以x和y不成比例;
故选:B。
【点睛】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
6.B
【分析】根据甲、乙两个圆的直径比是2∶3,可以设在图上甲圆的直径是2d,乙圆的直径是3d。根据实际距离=图上距离÷比例尺,分别求出两个圆的实际直径,之后再把两个圆实际的直径进行比即可。
【详解】设图上甲圆直径是2d,乙圆直径为3d。
甲圆实际直径:2d÷=16d
乙圆实际直径:3d÷=24d
16d∶24d=2∶3
故答案为:B
【点睛】此题主要考查了利用比例尺解决问题的方法。
7. 1 正
【分析】根据圆锥的认识即可知道,圆锥只有一条高,顶点到底面圆心的距离;根据圆锥的体积公式:V=Sh,当高一定,则=h(一定),根据正比例的判断方法,两个相关联的量的比值一定,则成正比例;反比例的判断方法:两个相关联的量的乘积一定,则成反比例。由此即可解答。
【详解】由分析可知,圆锥有1条高。
如果高一定,它的体积与底面积成正比例。
【点睛】本题主要考查圆锥的认识以及正比例和反比例的判断方法,熟练掌握正比例和反比例的判断方法并灵活运用。
8. 反 正
【分析】两个相关联的量,如果它们的比值一定,则成正比例关系;如果它们的乘积一定,则成反比例关系。据此解答。
【详解】车轮的周长×车轮需要转动的圈数=行驶的路程(一定),所以行驶的路程一定,车轮的周长与车轮需要转动的圈数成反比例。
正方体的表面积÷一个面的面积=6,正方体的表面积与它的一个面的面积比值一定,成正比例。
【点睛】此题考查了正反比例的辨别,主要看两个相关联的量是比值一定还是乘积一定。
9. 8 1.2 正
【分析】当字母的数值确定时,把它代入含有字母的式子中进行计算;判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】当x=2时,y=4×2=8;
当y=4.8时,x=4.8÷4=1.2;
y=4x,即=4,比值一定,所以x与y成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
10. 32 18
【分析】比值一定的两个量成正比例关系;乘积一定的两个量成反比例关系。根据比例关系列出比例,再解比例即可。
【详解】如果x和y成正比例,
解:设“?”处填x,
24∶3=x∶4
3x=96
x=32
如果x和y成反比例,
解:设“?”处应填x,
4x=24×3
4x=72
x=18
【点睛】本题考查两种比例关系的意义。根据比例关系列出正确的比例方程是解答此题的关键。
11.正
【分析】判断x和y是否成比例,就看这两种量是否是对应的乘积(商)一定,如果是乘积(商)一定,就成反(正)比例,如果不是乘积(商)一定或乘积(商)不一定,就不成比例。
【详解】因为x∶7=y∶6(x≠0,y≠0),所以x∶y=7∶6,即x∶y=(比值一定),所以x和y成正比例关系。
【点睛】此题考查用正反比例的意义辨识成正比例的量与成反比例的量,灵活应用比例的基本性质是解题的关键。
12. 正 4 750
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。题目中路程÷时间=速度,通过读图和计算,判断速度是否一定即可。
(2)由图可直接得到快车追上慢车的时间。
(3)求出的慢车的速度,从图中又知道了慢车走完全程用的时间,因此,可以得出A、B两地的路程。
【详解】(1)100÷2=50(千米/时),300÷6=50(千米/时),结合图可知,慢车在匀速行驶,即速度是一定的,路程÷时间=速度(一定),所以慢车所行的路程和时间成正比例。
(2)快车从慢车出发后2小时出发,6小时的时候追上慢车,用了6-2=4小时追上慢车。
(3)由第(1)知道慢车的速度为50千米/时,慢车行驶完全程用了15小时,则A、B两地的路程是:50×15=750千米
【点睛】本题考查了学生识图、读图、从图中获取信息的能力,通过图中信息计算出慢车的速度是解答本题的关键。
13. 5 40 30 12 荔枝总颗数 反
【分析】一箱荔枝的颗数是一定的,每人分的颗数×可分的人数=荔枝的总颗数(一定),据此填表解答。
【详解】(1)1×120=2×60=120
120÷24=5(颗)
120÷3=40(人)
120÷4=30(人)
120÷10=12(人)
(2)从表格中可以看出,荔枝总颗数不变。
(3)每人分的颗数与可分的人数成反比例关系。
【点睛】此题主要考查了反比例的意义与辨别,认真解答即可。
14. 2.5 12.5 25
【分析】根据题目可知,84消毒液∶清水=1∶200=,由此即可知道84消毒液和清水成的比值一定,则84消毒液和清水成正比例,84消毒液=×清水,即当清水是500克、2500克、5000克分别代入公式求出相应的84消毒液的毫升,由此即可解答。
【详解】由分析可知,84消毒液和清水成正比例
当加清水500克,需要84消毒液:500×=2.5(毫升);
当加清水2500克,需要84消毒液:2500×=12.5(毫升)
当加清水5000克,需要84消毒液:5000×=25(毫升)
【点睛】本题主要考查正比例的辨识以及正比例的应用,熟练掌握正比例的意义并灵活运用。
15.√
【详解】总价÷份数=单价(一定),总价和份数的商一定,二者成正比例,原题说法正确.
故答案为:正确
【点睛】根据数量关系判断总价和份数的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例
16.×
【解析】略
17.×
【解析】略
18.√
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y∶x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此解答;根据题意,先推导出x与y的比值,比值一定时,成正比例,乘积一定时,成反比例,据此判断。
【详解】已知5x-3y=0,则x∶y=, 那么x与y成正比例,原题说法正确。
故答案为:√
19.√
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。
【详解】正比例的图象是一条直线,说法正确。
故答案为:√
【点睛】本题考查正比例的意义及图象的特点,属于基础题。
20.;;
【分析】方程左边计算后是,根据等式的性质,方程两边同时除以1.2;
根据等式的性质,方程两边同时加4.6,再同时除以0.8;
将比例式化成方程式是,根据等式的性质,方程两边同时除以84。
【详解】
解:
解:
解:
21.1260米
【分析】题中有速度和时间两种相关联的量,小东走路的速度×时间=家到学校的路程(一定),乘积一定,则小东走路的速度和时间成反比例。设小东准时到达需x分钟,根据比例关系列方程解答。求出准时到达的时间后,再减去5分钟求出每分走70米时所用的时间,最后乘70即可求出小东家到学校的路程是多少米。
【详解】解:设准时到达需x分钟。
70×(x-5)=45×(x+5)
70x-350=45x+225
70x-45x=225+350
25x=575
x=23
70×(23-5)
=70×18
=1260(米)
答:小东家到学校的路程是1260米。
【点睛】本题总路程不变,用比例知识来解时,明确小东走路的速度和时间成反比例是解题的关键。
22.(1)30;37.5
(2)时间;路程;速度
(3)成正比例;因为路程÷时间=速度,那么当速度一定时,行驶的路程与所需时间成正比例。
【分析】(1)根据路程、时间、速度三者之间的关系:路程÷时间=速度、路程=时间×速度即可完成填空;
(2)根据数据可分析出,路程随着时间的变化而变化,不变的量是速度;
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定:如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)15÷2=7.5(千米/分),4×7.5=30(千米),5×7.5=37.5(千米)
填表如下:
时间/分 1 2 3 4 5 …
路程/千米 7.5 15 22.5 ( 30 ) ( 37.5) …
(2)表中两种变化的量是时间和路程,不变的量是速度;
(3)这列磁悬浮列车行驶的路程和所需时间成正比例;因为路程÷时间=速度,那么当速度一定时,行驶的路程与所需时间成正比例。
【点睛】辨识成正、反比例的量的关键就是看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
23.455.4元
【分析】题中有总价和数量两种相关联的量,且=单价(一定),比值一定,则茶叶的总价和数量成正比例。设李叔叔应付x元,根据比例关系用方程解答。
【详解】500克=0.5千克
解:设李叔叔应付x元。
x∶2.3=99∶0.5
0.5x=99×2.3
0.5x=227.7
x=455.4
答:应付455.4元。
【点睛】用比例知识解题时,明确“单价一定,总价和数量成正比例关系”是解题的关键。
24.(1)见详解
(2)根据表格发现:长方形的一条边不变,长方形的面积随着另一条边的变化而变化。
(3)长方形的长与面积成正比例,因为面积与一条边长度的比值一定。
【分析】(1)根据长方形面积公式S=ab,通过计算完成表格;
(2)根据表格中的数据发现长方形的一条边不变,长方形的面积随着另一条边的变化而变化;
(3)根据面积与长的比值一定,判断长方形的面积与长成正比例。
【详解】(1)(平方厘米)
(平方厘米)
(平方厘米)
(平方厘米)
填表如下:
面积 3 6 9 12 30
长 1 2 3 4 10
(2)根据表格发现:
长方形的一条边不变,长方形的面积随着另一条边的变化而变化。
(3)3÷1=6÷2=9÷3=12÷4=30÷10=3(一定),所以长方形的长与面积成正比例。
【点睛】此题主要考查正比例的意义,以及长方形的面积公式的应用。
25.(1)50.24;78.5;
(2)表中半径和面积都在变化。
(3)圆的面积与半径的平方的比值为(一定),
所以圆的面积与半径的平方成正比例,
即圆的面积随着半径的平方的变化而变化。
【分析】根据圆的面积计算公式,代入数据计算;观察表格,可以发现表中的半径和面积均在变化,依据圆的面积计算公式可知(一定),据此进行分析即可。
【详解】(1)(平方厘米)
(平方厘米)
统计表如下:
半径 1 2 3 4 5
面积 3.14 12.56 28.26 50.24 78.5
(2)表中半径和面积都在变化。
(3)圆的面积与半径的平方的比值为(一定),
所以圆的面积与半径的平方成正比例,
即圆的面积随着半径的平方的变化而变化。
【点睛】本题考查了圆的面积与半径之间的关系。判断的关键在于掌握圆的面积计算公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第4单元正比例与反比例重难点检测卷(单元测试)-小学数学六年级下册北师大版
一、选择题
1.微信朋友圈的总人数一定,朋友圈内点赞人数的数量与未点赞人数的数量( )比例。
A.成正 B.成反 C.不成 D.无法确定
2.圆锥的体积一定,它的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.一个圆的半径与它的周长( )。
A.成正比例 B.成反比例 C.不成比例 D.没有关系
4.下列变化的量中,成反比例的是( )。
A.长方形的长一定,宽和面积 B.一袋大米,吃去的数量和剩下的数量
C.4a=5b(a、b不为0),那么a和b D.平行四边形的面积不变,它的底与高
5.下面几个关系中,x和y(x、y不为0)成反比例关系的是( )。
A. B. C. D.
6.在比例尺是1∶8的图纸上,甲、乙两个圆的直径比是2∶3,那么甲、乙两个圆实际的直径比是( )。
A.1∶8 B.2∶3 C.4∶9 D.9∶4
二、填空题
7.一个圆锥有( )条高,如果高一定,它的体积与底面积成( )比例。
8.行驶的路程一定,车轮的周长与车轮需要转动的圈数成( )比例。正方体的表面积与它的一个面的面积成( )比例。
9.已知y=4x,当x=2时,y=( );当y=4.8时,x=( ),x与y成( )比例。
10.如果下表x和y成正比例,那么“?”处应填( );如果x和y成反比例,那么“?”处应填( )。
x 24 ?
y 3 4
11.因为x∶7=y∶6(x≠0,y≠0),所以x和y成( )比例。
12.慢车和快车沿相同的路线从地到地所行路程和时间的关系如图所示:
(1)慢车行驶时间和路程成( )比例关系。
(2)快车追上慢车所需时间是( )小时。
(3)、两地之间的路程是( )千米。
13.一箱荔枝,平均分给一些小朋友。
每人分的颗数 1 2 3 4 ( ) 10
可分的人数 120 60 ( ) ( ) 24 ( )
(1)完成表格。
(2)从表格中可以看出,( )不变。
(3)每人分的颗数与可分的人数成( )比例关系。
14.84消毒液是一种无色或淡黄色的液体,是一种高效消毒剂。疫情期间被广泛用于宾馆、旅游、医院、家庭、学校等的卫生消毒,消毒方法:擦拭,喷洒,拖洗消毒。常用的有1∶500和1∶200两种84消毒液配制方法。
1∶500的84消毒液配制如下:
加清水 500克 2500克 5000克
84消毒液 1毫升 5毫升 10毫升
假如现在是1∶200的84消毒液配制,请完成下表:
加清水 500克 2500克 5000克
84消毒液 _____毫升 _____毫升 _____毫升
三、判断题
15.报刊的单价一定,报刊的份数和总价成正比例。 ( )
16.每年体检,班里近视的人数和不近视的人数成反比例。 ( )
17.花生的出油率一定,油的质量和花生的质量成反比例。 ( )
18.已知5x-3y=0,那么x与y成正比例。( )
19.正比例图象是一条直线。( )
四、计算题
20.解方程。
五、解答题
21.小东从家出发去学校,如果每分走70米,能在上课前5分到校;如果每分走45米,就要迟到5分。那么小东家到学校的路程是多少米?
22.一列磁悬浮列车匀速行驶,其所用时间和行驶路程关系如下表。
(1)把下表填写完整。
时间/分 1 2 3 4 5 …
路程/千米 7.5 15 22.5 ( ) ( ) …
(2)表中两种变化的量是( )和( ),不变的量是( )。
(3)这列磁悬浮列车行驶的路程和所需时间是否成正比例或反比例?为什么?
23.一种茶叶500克售价99元,李叔叔要买2.3千克这种茶叶,应付多少元?(用比例知识解答)
24.长方形的一条边长度是。
(1)把表填完整。
面积 3
长 1 2 3 4 10
(2)从表中你发现了什么规律?
(3)长方形的长与面积成正比例吗?为什么?
25.圆的半径与它的面积变化情况如表。
半径 1 2 3 4 5
面积 3.14 12.56 28.26 ( ) ( )
(1)把上表填完整。
(2)上表中哪些量在发生变化?
(3)圆的面积是如何随着半径的变化而变化的?
参考答案:
1.C
【分析】两个相关联的量,如果它们的比值一定,成正比例关系;如果它们的乘积一定,成反比例关系,据此解答。
【详解】点赞人数的数量+未点赞人数的数量=朋友圈的总人数(一定),和一定,不成比例。
故答案为:C
【点睛】判断两个相关联的两个量成什么比例,主要看它们是比值一定还是乘积一定。
2.B
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例。根据:圆锥的体积=底面积×高×,可知底面积与高的乘积是圆锥体积的,即是乘积一定,所以是反比例。
【详解】根据:圆锥的体积=底面积×高×,可知底面积与高的乘积是圆锥体积的;所以,圆锥的体积一定,它的底面积和高成反比例。
故答案为:B
【点睛】熟记圆锥的体积就是公式是解答此题的关键。
3.A
【分析】两个相关联的量,如果它们的比值一定,成正比例关系;如果它们的乘积一定,成反比例关系,据此解答。
【详解】 =2π,因为2π是定值,也就是周长与半径的比值一定,所以成正比例关系。
故选择:A
【点睛】此题考查了正、反比例的辨别,主要看两个量是比值一定还是乘积一定。
4.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.长方形的长一定,宽和面积比值一定,成正比例;
B.一袋大米,吃去的数量和剩下的数量,不成比例;
C.4a=5b(a、b不为0),那么a和b比值一定,成正比例;
D.平行四边形的面积不变,它的底与高乘积一定,成反比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5.B
【分析】判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。
【详解】A.因为:(一定),所以x和y成正比例,不合题意;
B.由比例的基本性质可知:x×y=10(一定),所以x和y成反比例,符合题意;
C.(一定),这是和一定,所以x和y不成比例;
D.由,得,即,所以x和y不成比例;
故选:B。
【点睛】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
6.B
【分析】根据甲、乙两个圆的直径比是2∶3,可以设在图上甲圆的直径是2d,乙圆的直径是3d。根据实际距离=图上距离÷比例尺,分别求出两个圆的实际直径,之后再把两个圆实际的直径进行比即可。
【详解】设图上甲圆直径是2d,乙圆直径为3d。
甲圆实际直径:2d÷=16d
乙圆实际直径:3d÷=24d
16d∶24d=2∶3
故答案为:B
【点睛】此题主要考查了利用比例尺解决问题的方法。
7. 1 正
【分析】根据圆锥的认识即可知道,圆锥只有一条高,顶点到底面圆心的距离;根据圆锥的体积公式:V=Sh,当高一定,则=h(一定),根据正比例的判断方法,两个相关联的量的比值一定,则成正比例;反比例的判断方法:两个相关联的量的乘积一定,则成反比例。由此即可解答。
【详解】由分析可知,圆锥有1条高。
如果高一定,它的体积与底面积成正比例。
【点睛】本题主要考查圆锥的认识以及正比例和反比例的判断方法,熟练掌握正比例和反比例的判断方法并灵活运用。
8. 反 正
【分析】两个相关联的量,如果它们的比值一定,则成正比例关系;如果它们的乘积一定,则成反比例关系。据此解答。
【详解】车轮的周长×车轮需要转动的圈数=行驶的路程(一定),所以行驶的路程一定,车轮的周长与车轮需要转动的圈数成反比例。
正方体的表面积÷一个面的面积=6,正方体的表面积与它的一个面的面积比值一定,成正比例。
【点睛】此题考查了正反比例的辨别,主要看两个相关联的量是比值一定还是乘积一定。
9. 8 1.2 正
【分析】当字母的数值确定时,把它代入含有字母的式子中进行计算;判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】当x=2时,y=4×2=8;
当y=4.8时,x=4.8÷4=1.2;
y=4x,即=4,比值一定,所以x与y成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
10. 32 18
【分析】比值一定的两个量成正比例关系;乘积一定的两个量成反比例关系。根据比例关系列出比例,再解比例即可。
【详解】如果x和y成正比例,
解:设“?”处填x,
24∶3=x∶4
3x=96
x=32
如果x和y成反比例,
解:设“?”处应填x,
4x=24×3
4x=72
x=18
【点睛】本题考查两种比例关系的意义。根据比例关系列出正确的比例方程是解答此题的关键。
11.正
【分析】判断x和y是否成比例,就看这两种量是否是对应的乘积(商)一定,如果是乘积(商)一定,就成反(正)比例,如果不是乘积(商)一定或乘积(商)不一定,就不成比例。
【详解】因为x∶7=y∶6(x≠0,y≠0),所以x∶y=7∶6,即x∶y=(比值一定),所以x和y成正比例关系。
【点睛】此题考查用正反比例的意义辨识成正比例的量与成反比例的量,灵活应用比例的基本性质是解题的关键。
12. 正 4 750
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。题目中路程÷时间=速度,通过读图和计算,判断速度是否一定即可。
(2)由图可直接得到快车追上慢车的时间。
(3)求出的慢车的速度,从图中又知道了慢车走完全程用的时间,因此,可以得出A、B两地的路程。
【详解】(1)100÷2=50(千米/时),300÷6=50(千米/时),结合图可知,慢车在匀速行驶,即速度是一定的,路程÷时间=速度(一定),所以慢车所行的路程和时间成正比例。
(2)快车从慢车出发后2小时出发,6小时的时候追上慢车,用了6-2=4小时追上慢车。
(3)由第(1)知道慢车的速度为50千米/时,慢车行驶完全程用了15小时,则A、B两地的路程是:50×15=750千米
【点睛】本题考查了学生识图、读图、从图中获取信息的能力,通过图中信息计算出慢车的速度是解答本题的关键。
13. 5 40 30 12 荔枝总颗数 反
【分析】一箱荔枝的颗数是一定的,每人分的颗数×可分的人数=荔枝的总颗数(一定),据此填表解答。
【详解】(1)1×120=2×60=120
120÷24=5(颗)
120÷3=40(人)
120÷4=30(人)
120÷10=12(人)
(2)从表格中可以看出,荔枝总颗数不变。
(3)每人分的颗数与可分的人数成反比例关系。
【点睛】此题主要考查了反比例的意义与辨别,认真解答即可。
14. 2.5 12.5 25
【分析】根据题目可知,84消毒液∶清水=1∶200=,由此即可知道84消毒液和清水成的比值一定,则84消毒液和清水成正比例,84消毒液=×清水,即当清水是500克、2500克、5000克分别代入公式求出相应的84消毒液的毫升,由此即可解答。
【详解】由分析可知,84消毒液和清水成正比例
当加清水500克,需要84消毒液:500×=2.5(毫升);
当加清水2500克,需要84消毒液:2500×=12.5(毫升)
当加清水5000克,需要84消毒液:5000×=25(毫升)
【点睛】本题主要考查正比例的辨识以及正比例的应用,熟练掌握正比例的意义并灵活运用。
15.√
【详解】总价÷份数=单价(一定),总价和份数的商一定,二者成正比例,原题说法正确.
故答案为:正确
【点睛】根据数量关系判断总价和份数的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例
16.×
【解析】略
17.×
【解析】略
18.√
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y∶x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此解答;根据题意,先推导出x与y的比值,比值一定时,成正比例,乘积一定时,成反比例,据此判断。
【详解】已知5x-3y=0,则x∶y=, 那么x与y成正比例,原题说法正确。
故答案为:√
19.√
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。
【详解】正比例的图象是一条直线,说法正确。
故答案为:√
【点睛】本题考查正比例的意义及图象的特点,属于基础题。
20.;;
【分析】方程左边计算后是,根据等式的性质,方程两边同时除以1.2;
根据等式的性质,方程两边同时加4.6,再同时除以0.8;
将比例式化成方程式是,根据等式的性质,方程两边同时除以84。
【详解】
解:
解:
解:
21.1260米
【分析】题中有速度和时间两种相关联的量,小东走路的速度×时间=家到学校的路程(一定),乘积一定,则小东走路的速度和时间成反比例。设小东准时到达需x分钟,根据比例关系列方程解答。求出准时到达的时间后,再减去5分钟求出每分走70米时所用的时间,最后乘70即可求出小东家到学校的路程是多少米。
【详解】解:设准时到达需x分钟。
70×(x-5)=45×(x+5)
70x-350=45x+225
70x-45x=225+350
25x=575
x=23
70×(23-5)
=70×18
=1260(米)
答:小东家到学校的路程是1260米。
【点睛】本题总路程不变,用比例知识来解时,明确小东走路的速度和时间成反比例是解题的关键。
22.(1)30;37.5
(2)时间;路程;速度
(3)成正比例;因为路程÷时间=速度,那么当速度一定时,行驶的路程与所需时间成正比例。
【分析】(1)根据路程、时间、速度三者之间的关系:路程÷时间=速度、路程=时间×速度即可完成填空;
(2)根据数据可分析出,路程随着时间的变化而变化,不变的量是速度;
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定:如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)15÷2=7.5(千米/分),4×7.5=30(千米),5×7.5=37.5(千米)
填表如下:
时间/分 1 2 3 4 5 …
路程/千米 7.5 15 22.5 ( 30 ) ( 37.5) …
(2)表中两种变化的量是时间和路程,不变的量是速度;
(3)这列磁悬浮列车行驶的路程和所需时间成正比例;因为路程÷时间=速度,那么当速度一定时,行驶的路程与所需时间成正比例。
【点睛】辨识成正、反比例的量的关键就是看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
23.455.4元
【分析】题中有总价和数量两种相关联的量,且=单价(一定),比值一定,则茶叶的总价和数量成正比例。设李叔叔应付x元,根据比例关系用方程解答。
【详解】500克=0.5千克
解:设李叔叔应付x元。
x∶2.3=99∶0.5
0.5x=99×2.3
0.5x=227.7
x=455.4
答:应付455.4元。
【点睛】用比例知识解题时,明确“单价一定,总价和数量成正比例关系”是解题的关键。
24.(1)见详解
(2)根据表格发现:长方形的一条边不变,长方形的面积随着另一条边的变化而变化。
(3)长方形的长与面积成正比例,因为面积与一条边长度的比值一定。
【分析】(1)根据长方形面积公式S=ab,通过计算完成表格;
(2)根据表格中的数据发现长方形的一条边不变,长方形的面积随着另一条边的变化而变化;
(3)根据面积与长的比值一定,判断长方形的面积与长成正比例。
【详解】(1)(平方厘米)
(平方厘米)
(平方厘米)
(平方厘米)
填表如下:
面积 3 6 9 12 30
长 1 2 3 4 10
(2)根据表格发现:
长方形的一条边不变,长方形的面积随着另一条边的变化而变化。
(3)3÷1=6÷2=9÷3=12÷4=30÷10=3(一定),所以长方形的长与面积成正比例。
【点睛】此题主要考查正比例的意义,以及长方形的面积公式的应用。
25.(1)50.24;78.5;
(2)表中半径和面积都在变化。
(3)圆的面积与半径的平方的比值为(一定),
所以圆的面积与半径的平方成正比例,
即圆的面积随着半径的平方的变化而变化。
【分析】根据圆的面积计算公式,代入数据计算;观察表格,可以发现表中的半径和面积均在变化,依据圆的面积计算公式可知(一定),据此进行分析即可。
【详解】(1)(平方厘米)
(平方厘米)
统计表如下:
半径 1 2 3 4 5
面积 3.14 12.56 28.26 50.24 78.5
(2)表中半径和面积都在变化。
(3)圆的面积与半径的平方的比值为(一定),
所以圆的面积与半径的平方成正比例,
即圆的面积随着半径的平方的变化而变化。
【点睛】本题考查了圆的面积与半径之间的关系。判断的关键在于掌握圆的面积计算公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
