【课堂讲义】2014年高中数学(必修1·A版)(入门答疑+思维启迪+状元随笔)同步课件:2-3 幂函数
文档属性
| 名称 | 【课堂讲义】2014年高中数学(必修1·A版)(入门答疑+思维启迪+状元随笔)同步课件:2-3 幂函数 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-05 15:34:32 | ||
图片预览









文档简介
课件46张PPT。2.3 幂函数[问题1] 如果圣诞节卡片每张1元,那么买x张卡片需y元,则x与y的关系是什么?
[提示] y=x.
[问题2] 如果正方形的边长为x,面积为y,则x与y的关系是什么?
[提示] y=x2.[提示] y=x-1.[提示] 共同点:均是幂的形式
不同点:第一组:底数是自变量
第二组:指数是自变量
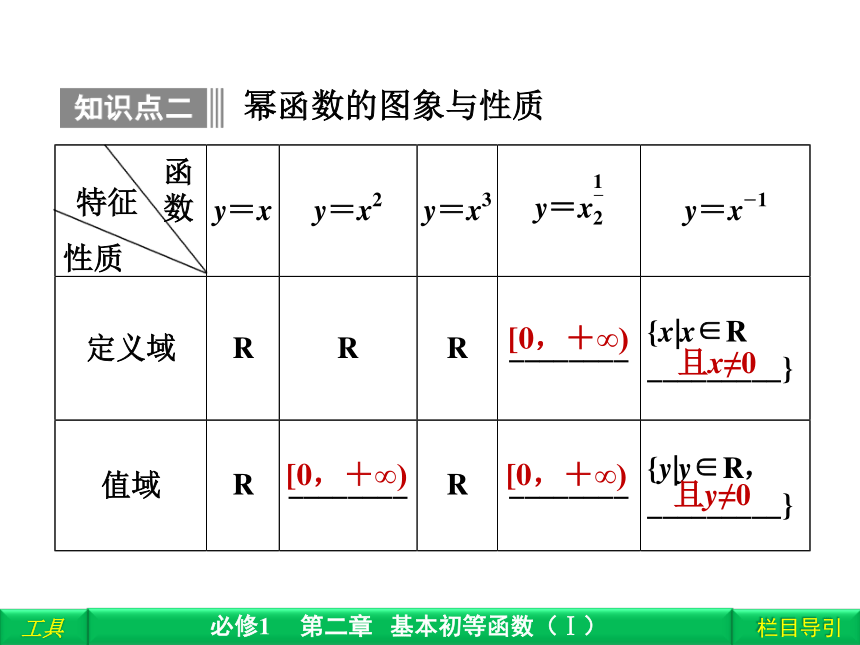
y=xαxα幂函数的概念幂函数与指数函数的区别性质函
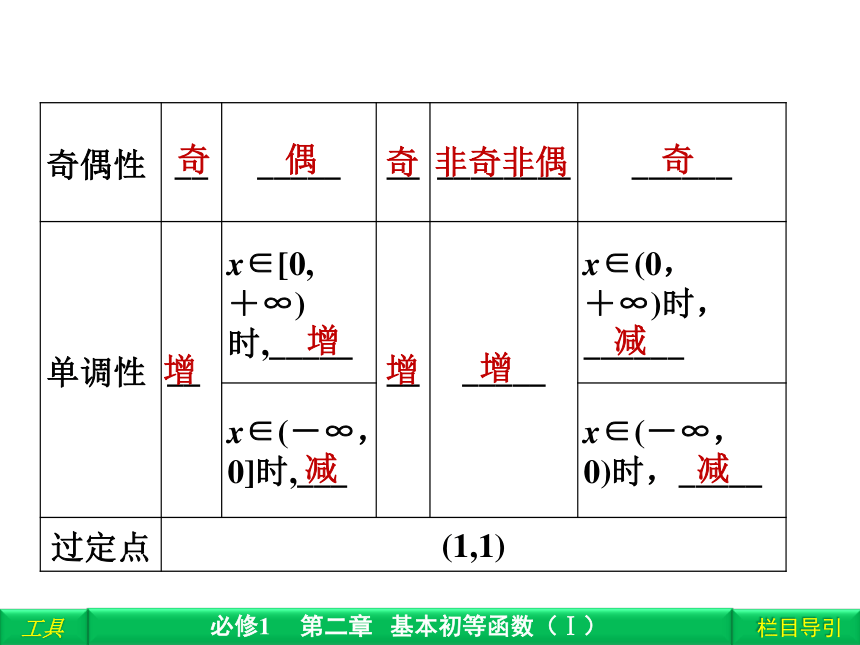
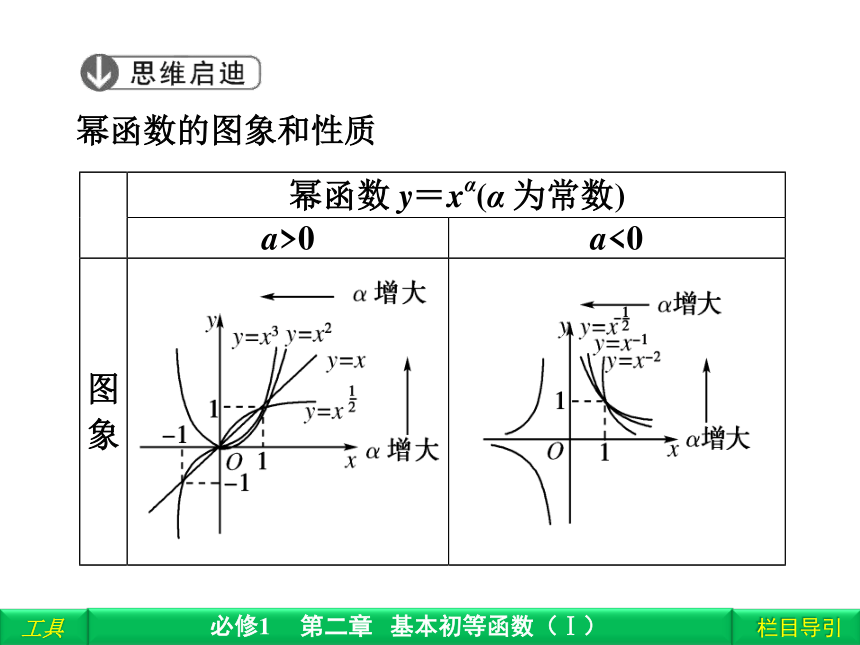
数特征[0,+∞)[0,+∞)[0,+∞)且x≠0且y≠0幂函数的图象与性质奇增偶增减奇增非奇非偶增奇减减幂函数的图象和性质1.下列结论正确的是( )
A.幂函数图象一定过原点
B.当α<0时,幂函数y=xα是减函数
C.当α>1时,幂函数y=xα是增函数
D.函数y=x2既是二次函数,也是幂函数
解析: 函数y=x-1的图象不过原点.故A不正确;y=x-1在(-∞,0)及(0,+∞)上是减函数,故B不正确;函数y=x2在(-∞,0)上是减函数.在(0,+∞)上是增函数.故C不正确.
答案: D答案: D答案: (1)< (2)< (3)> (4)< (5)> (6)>函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.
[思路点拨] 首先根据幂函数的定义,幂的系数为1,其次根据性质确定m的值,进而得解.根据幂函数定义得m2-m-1=1,
解得m=2或m=-1,
当m=2时,f(x)=x3在(0,+∞)上是增函数,
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,不合要求.
故f(x)=x3.答案: B幂函数的图象已知函数y=xa,y=xb,y=xc的图象如图所示,则a,b,c的大小关系为( )
A.cC.b0,b>0.
由幂函数的性质知,当x>1时,幂指数大的幂函数的函数值就大,则a>b.
综上所述,可知c答案: A幂函数的性质比较两个幂的大小的关键是搞清底数与指数是否相同,若底数相同,利用指数函数的性质比较大小;若指数相同,利用幂函数的性质比较大小;若底数、指数均不同,考虑用中间值法. [思路点拨] (1)解决与幂函数有关的综合性问题时,一定要考虑幂函数的定义.对于幂函数y=xα,由于α值不同,所以其单调性和奇偶性不同.
(2)常见的求解幂函数的解析式的思路是利用幂函数的性质和已知条件得到幂指数满足的条件,从而求得解析式.与幂函数有关的综合性问题一般为利用单调性、奇偶性以及图象求解函数值域、不等式的解集等. [练规范、练速度、练技能]
[提示] y=x.
[问题2] 如果正方形的边长为x,面积为y,则x与y的关系是什么?
[提示] y=x2.[提示] y=x-1.[提示] 共同点:均是幂的形式
不同点:第一组:底数是自变量
第二组:指数是自变量
y=xαxα幂函数的概念幂函数与指数函数的区别性质函
数特征[0,+∞)[0,+∞)[0,+∞)且x≠0且y≠0幂函数的图象与性质奇增偶增减奇增非奇非偶增奇减减幂函数的图象和性质1.下列结论正确的是( )
A.幂函数图象一定过原点
B.当α<0时,幂函数y=xα是减函数
C.当α>1时,幂函数y=xα是增函数
D.函数y=x2既是二次函数,也是幂函数
解析: 函数y=x-1的图象不过原点.故A不正确;y=x-1在(-∞,0)及(0,+∞)上是减函数,故B不正确;函数y=x2在(-∞,0)上是减函数.在(0,+∞)上是增函数.故C不正确.
答案: D答案: D答案: (1)< (2)< (3)> (4)< (5)> (6)>函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.
[思路点拨] 首先根据幂函数的定义,幂的系数为1,其次根据性质确定m的值,进而得解.根据幂函数定义得m2-m-1=1,
解得m=2或m=-1,
当m=2时,f(x)=x3在(0,+∞)上是增函数,
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,不合要求.
故f(x)=x3.答案: B幂函数的图象已知函数y=xa,y=xb,y=xc的图象如图所示,则a,b,c的大小关系为( )
A.c
由幂函数的性质知,当x>1时,幂指数大的幂函数的函数值就大,则a>b.
综上所述,可知c
(2)常见的求解幂函数的解析式的思路是利用幂函数的性质和已知条件得到幂指数满足的条件,从而求得解析式.与幂函数有关的综合性问题一般为利用单调性、奇偶性以及图象求解函数值域、不等式的解集等. [练规范、练速度、练技能]
