【课堂讲义】2014年高中数学(必修1·A版)(入门答疑+思维启迪+状元随笔)同步课件:第三章 函数的应用 章末高效整合
文档属性
| 名称 | 【课堂讲义】2014年高中数学(必修1·A版)(入门答疑+思维启迪+状元随笔)同步课件:第三章 函数的应用 章末高效整合 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-05 15:37:48 | ||
图片预览











文档简介
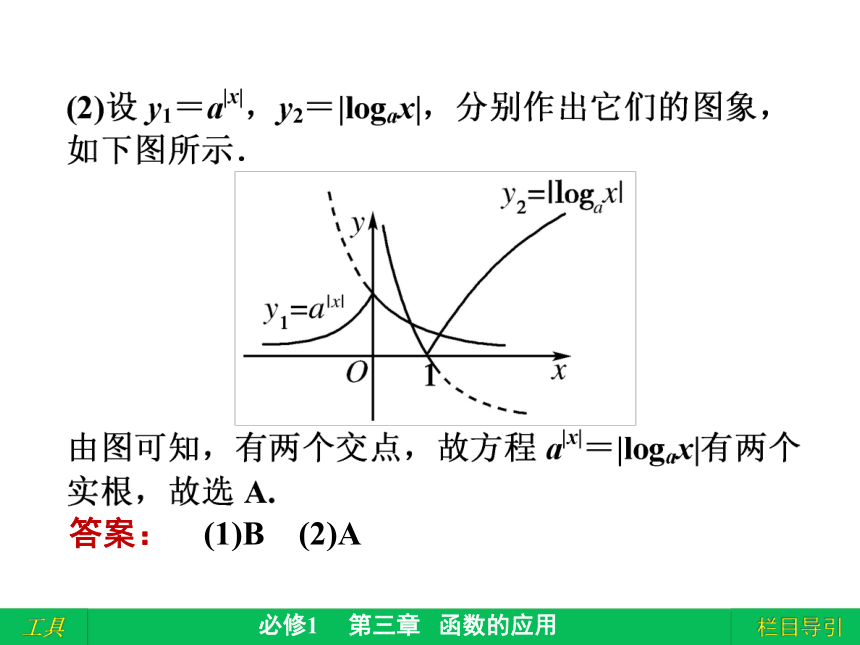
课件45张PPT。函数的零点与方程的根的关系及应用答案: (1)B (2)A1.(1)方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
(2)若方程|ax|=x+a(a>0)有两个解,则a的取值范围是( )
A.(1,+∞) B.(0,1)
C.(0,+∞) D.?答案: (1)C (2)A
用二分法求函数的零点或方程的近似解由于|0.687 5-0.75|=0.062 5<0.1,所以0.75可作为方程的一个正实数近似解.2.求函数f(x)=x3+2x2-3x-6的一个正数零点.(精确度为0.1)
由于|1.75-1.687 5|=0.062 5<0.1,
所以可将1.75作为函数零点的近似值.解析: 由于f(1)=-6<0,f(2)=4>0,可取区间(1,2)作为计算的初始区间,用二分法逐次计算,列表如下:函数模型及应用2.解函数应用问题常见的错误以及克服的关键:
(1)不会将实际问题抽象转化为函数模型或转化不全面;
(2)在求解过程中忽略实际问题对变量参数的限制条件.
克服的关键在于深入理解题意,用变化的观点分析和探求具体问题中的数量关系,寻求已知量与未知量之间的内在联系,然后将这些内在联系与数学知识结合起来,建立函数关系式或列出方程,利用函数性质或方程观点来求解.某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系如图(1)所示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下:
(1)根据提供的图象,写出该商品每件的销售价格P与时间t的函数关系式;[思维点击] 首先由图象求出销售价格P与时间t的函数关系式,其次求出日销售量Q与时间t的一个函数关系式,并在此基础上利用关系:日销售金额=销售价格P×日销售量Q,求出日销售金额的函数式.3.某星级旅馆有150个标准房,经过一段时间的经营,经理得到一些定价和住房率的数据如下:欲使每天的营业额最高,应如何定价?1.若x0是方程ln x+x=4的解,则x0属于区间( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
解析: 构造函数f(x)=ln x+x-4,则函数f(x)的图象是连续不断的一条曲线,又f(2)=ln 2+2-4<0,f(3)=ln 3+3-4>0,所以f(2)·f(3)<0,故函数的零点所在区间为(2,3),即方程ln x+x=4的解x0属于区间(2,3),故选C.
答案: C答案: B3.当x∈(4,+∞)时,f(x)=x2,g(x)=2x,h(x)=log2x的大小关系是( )
A.f(x)>g(x)>h(x) B.g(x)>f(x)>h(x)
C.g(x)>h(x)>f(x) D.f(x)>h(x)>g(x)答案: B4.一个商人有一批货,如果月初售出可获利1 000元,再将收益都存入银行,已知银行月息为2.4%;如果月末售出可获利1 200元,但要付50元货物保管费.这个商人若要获得最大收益,则这批货( )
A.月初售出好
B.月末售出好
C.月初或月末一样
D.由成本费的大小确定出售时机答案: D5.已知定义在R上的函数f(x)的图象是连续不断的,且有如下部分对应值表:可以看出函数至少有________个零点.
解析: 由于f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,所以函数至少有3个零点.
答案: 36.某位股民购进某支股票,在接下来的交易时间内,他的这支股票先经历了n次涨停(每次上涨10%),又经历了n次跌停(每次下跌10%),则该股民这支股票的盈亏情况(不考虑其他费用)为( )
A.略有盈利 B.略有亏损
C.没有盈利也没有亏损 D.无法判断盈亏情况
解析: 设该股民购这支股票的价格为a,则经历n次涨停后的价格为a(1+10%)n=a×1.1n,经历n次跌停后的价格为a×1.1n×(1-10%)n=a×1.1n×0.9n=a×(1.1×0.9)n=0.99n·a答案: B8.某市自来水收费标准如下:每户每月用水不超过4t时,每吨为1.80元,当用水超过4t时,超过部分每吨3.00元,某月甲,乙两用户共交水费y元,已知甲,乙两用户该月用水量分别为5x,3x.
(1)求y关于x的函数.
(2)若甲,乙两用户该月共交水费26.4元,分别求出甲,乙两用户该月的用水量和水费.[练规范、练速度、练技能]
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
(2)若方程|ax|=x+a(a>0)有两个解,则a的取值范围是( )
A.(1,+∞) B.(0,1)
C.(0,+∞) D.?答案: (1)C (2)A
用二分法求函数的零点或方程的近似解由于|0.687 5-0.75|=0.062 5<0.1,所以0.75可作为方程的一个正实数近似解.2.求函数f(x)=x3+2x2-3x-6的一个正数零点.(精确度为0.1)
由于|1.75-1.687 5|=0.062 5<0.1,
所以可将1.75作为函数零点的近似值.解析: 由于f(1)=-6<0,f(2)=4>0,可取区间(1,2)作为计算的初始区间,用二分法逐次计算,列表如下:函数模型及应用2.解函数应用问题常见的错误以及克服的关键:
(1)不会将实际问题抽象转化为函数模型或转化不全面;
(2)在求解过程中忽略实际问题对变量参数的限制条件.
克服的关键在于深入理解题意,用变化的观点分析和探求具体问题中的数量关系,寻求已知量与未知量之间的内在联系,然后将这些内在联系与数学知识结合起来,建立函数关系式或列出方程,利用函数性质或方程观点来求解.某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系如图(1)所示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下:
(1)根据提供的图象,写出该商品每件的销售价格P与时间t的函数关系式;[思维点击] 首先由图象求出销售价格P与时间t的函数关系式,其次求出日销售量Q与时间t的一个函数关系式,并在此基础上利用关系:日销售金额=销售价格P×日销售量Q,求出日销售金额的函数式.3.某星级旅馆有150个标准房,经过一段时间的经营,经理得到一些定价和住房率的数据如下:欲使每天的营业额最高,应如何定价?1.若x0是方程ln x+x=4的解,则x0属于区间( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
解析: 构造函数f(x)=ln x+x-4,则函数f(x)的图象是连续不断的一条曲线,又f(2)=ln 2+2-4<0,f(3)=ln 3+3-4>0,所以f(2)·f(3)<0,故函数的零点所在区间为(2,3),即方程ln x+x=4的解x0属于区间(2,3),故选C.
答案: C答案: B3.当x∈(4,+∞)时,f(x)=x2,g(x)=2x,h(x)=log2x的大小关系是( )
A.f(x)>g(x)>h(x) B.g(x)>f(x)>h(x)
C.g(x)>h(x)>f(x) D.f(x)>h(x)>g(x)答案: B4.一个商人有一批货,如果月初售出可获利1 000元,再将收益都存入银行,已知银行月息为2.4%;如果月末售出可获利1 200元,但要付50元货物保管费.这个商人若要获得最大收益,则这批货( )
A.月初售出好
B.月末售出好
C.月初或月末一样
D.由成本费的大小确定出售时机答案: D5.已知定义在R上的函数f(x)的图象是连续不断的,且有如下部分对应值表:可以看出函数至少有________个零点.
解析: 由于f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,所以函数至少有3个零点.
答案: 36.某位股民购进某支股票,在接下来的交易时间内,他的这支股票先经历了n次涨停(每次上涨10%),又经历了n次跌停(每次下跌10%),则该股民这支股票的盈亏情况(不考虑其他费用)为( )
A.略有盈利 B.略有亏损
C.没有盈利也没有亏损 D.无法判断盈亏情况
解析: 设该股民购这支股票的价格为a,则经历n次涨停后的价格为a(1+10%)n=a×1.1n,经历n次跌停后的价格为a×1.1n×(1-10%)n=a×1.1n×0.9n=a×(1.1×0.9)n=0.99n·a
(1)求y关于x的函数.
(2)若甲,乙两用户该月共交水费26.4元,分别求出甲,乙两用户该月的用水量和水费.[练规范、练速度、练技能]
