人教版(2023春)数学六年级下册6.4比和比例 课件(25张PPT)
文档属性
| 名称 | 人教版(2023春)数学六年级下册6.4比和比例 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
第6单元 整理和复习
第4节 比和比例
一、情境引入
四个长方形中你觉得哪一个与众不同呢
一、情境引入
为什么呢 谁能用数学知识来说明原因?
第一个:长25 cm,宽20 cm。
第二个:长15 cm,宽12 cm。
第三个:长20 cm,宽16 cm。
第四个:长24 cm,宽9 cm。
比和比例
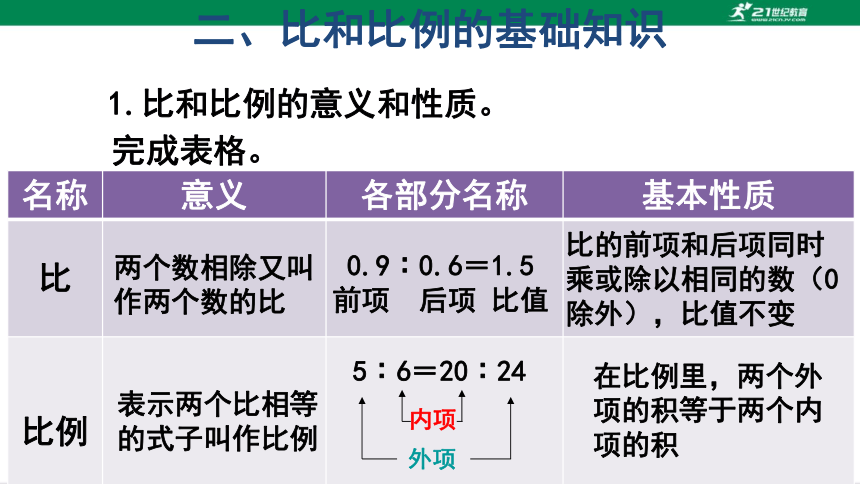
二、比和比例的基础知识
1.比和比例的意义和性质。
完成表格。
名称 意义 各部分名称 基本性质
比
比例
两个数相除又叫作两个数的比
表示两个比相等的式子叫作比例
0.9∶0.6=1.5
前项 后项 比值
5∶6=20∶24
内项
外项
比的前项和后项同时乘或除以相同的数(0除外),比值不变
在比例里,两个外项的积等于两个内项的积
(1)六年级男生有80人,女生有84人,男生与女生人数之比为_______。
(2)小明身高160 cm,他一庹长也是160 cm,二者之比为____。
(3)小丽的脚长23 cm,她的身高是161 cm,她的脚长与身高之比为____。
(4)如果3a=5b(a、b≠0),那么a:b=____。
20:21
1:1
1:7
5:3
求比值和化简比有什么联系和区别?
求比值 化简比
意义
方法
结果
前项除以后项的商
把比的前项和后项化成最简整数比
前项 ÷ 后项
运用比的基本性质
是一个数(可以是分数、小数或整数)
仍是一个比
比与分数、除法有什么联系 请大家先填写教材第2题的表格,再说一说它们的区别。
2.比与分数、除法的关系。
名称 各个部分 化简比
分数
除法
比
分子
分数线
分母
分数值
被除数
除号÷
除数
商
4÷2=2
前项
比号:
后项
比值
6:3=2
a÷b=a:b(b≠0)。
你能用字母来表示比与分数、除法之间的关系吗?
想一想,比与分数、除法有什么区别?
比指的是两个数的关系,分数是一个数,除法是一种运算。
3.比的基本性质、分数的基本性质和商不变的规律之间的联系。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
商不变的规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
结合比与分数、除法之间的联系,你能说说比的基本性质、分数的基本性质和商不变的规律之间有什么样的联系吗?
比的前项相当于分数中的分子、除法中的被除数,比号相当于分数中的分数线、除法中的除号,比的后项相当于分数中的分母、除法中的除数,比值相当于分数中的分数值、除法中的商,所以它们的变化规律是一样的。
我们在应用这些性质和规律时,都是将各部分同时乘或除以一个相同的数(0除外),结果不变。
练习:
9:4=4.5:x
x:2.6=3:
x
x=20.8
x=2
x=
练习:
妈妈和面做面条,一共做了1.8 kg,面粉和水的质量比是7:2。面粉和水分别用了多少千克?
1.8×=1.4(kg)
1.8×=0.4(kg)
答:面粉用了1.4 kg,水用了0.4 kg。
练习:
一块金牌重412 g,其中所含的黄金质量与金牌总质量的比为3:206,做302块这样的金牌需要黄金多少克?
412××302=1812(克)
答:做302块这样的金牌需要黄金1812克。
4.正、反比例的意义
发芽率一定,发芽的种子数与种子的总数。
圆柱的侧面积一定,它的底面半径和高。
订阅某报的份数和钱数。
判断下列相关联的两种量是否成比例,成什么比例。
正比例
反比例
正比例
想一想,你是怎么判断相关联的两个量成正比例关系或成反比例关系的呢?
你能用字母来表示正、反比例的意义吗
正比例关系:=k(一定)
反比例关系:xy=k(一定)
说一说正比例和反比例有什么相同点和不同点。
正比例 反比例
相同点 不同点
1.都是描述两种相关联的量。
2.一种量随着另一种量的变化而变化
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
2.相对应的每两个数的比值(商) 是一定的。
3.关系式:=k(一定)
1.变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2.相对应的每两个数的乘积是一定的。
3.关系式:x×y=k(一定)
练习
1.判断下面各题中的两个量是否成正比例或反比例关系。
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知=3,y与x。
(3)三角形的面积一定,它的底与高。
(4)正方体的表面积与它的一个面的面积。
(5)已知xy=1,y与x。
(6)出油率一定,花生油的质量与花生的质量。
不成比例
成正比例
成反比例
成正比例
成反比例
成正比例
已知一辆汽车3小时行135 km,照这样计算,这辆汽车6小时行多少千米
“六一”儿童节,某小学表演大型团体操。原计划站36行,正好每行站24人。后来改站32行,每行能站多少人
比一比,想一想,这两道题有什么不同? 能用比例方法解答吗
用比例方法解决问题的步骤和关键是什么
①根据不变量,判断题中哪两种相关联的量成正比例或反比例。
②找出两组相对应的数,并设出未知数,列出比例。
③解比例。
④检验并写出答语。
在同一幅地图上,量得甲、乙两地的距离是20 cm,甲、丙两地的距离是12 cm。如果甲、乙两地的实际距离是1600 km,那么甲、丙两地的实际距离是多少
解:设甲、丙两地的实际距离是x km 。
20∶1600=12∶x
x=960
答:甲、丙两地的实际距离是960 km。
三、综合应用,提升能力
甲地到乙地的高速公路大约长200 km,乙地到丙地的高速公路大约长280 km。一辆汽车从甲地出发经乙地开往丙地,当行驶到乙地时用了2.5小时。按照这个速度,该车从甲地到丙地大约需要多少小时
280÷(200÷2.5)=3.5(h)
2.5+3.5=6(h)
答:该车从甲地到丙地大约需要6小时。
四、课堂小结
回顾今天的复习过程,你们有什么收获呢?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第6单元 整理和复习
第4节 比和比例
一、情境引入
四个长方形中你觉得哪一个与众不同呢
一、情境引入
为什么呢 谁能用数学知识来说明原因?
第一个:长25 cm,宽20 cm。
第二个:长15 cm,宽12 cm。
第三个:长20 cm,宽16 cm。
第四个:长24 cm,宽9 cm。
比和比例
二、比和比例的基础知识
1.比和比例的意义和性质。
完成表格。
名称 意义 各部分名称 基本性质
比
比例
两个数相除又叫作两个数的比
表示两个比相等的式子叫作比例
0.9∶0.6=1.5
前项 后项 比值
5∶6=20∶24
内项
外项
比的前项和后项同时乘或除以相同的数(0除外),比值不变
在比例里,两个外项的积等于两个内项的积
(1)六年级男生有80人,女生有84人,男生与女生人数之比为_______。
(2)小明身高160 cm,他一庹长也是160 cm,二者之比为____。
(3)小丽的脚长23 cm,她的身高是161 cm,她的脚长与身高之比为____。
(4)如果3a=5b(a、b≠0),那么a:b=____。
20:21
1:1
1:7
5:3
求比值和化简比有什么联系和区别?
求比值 化简比
意义
方法
结果
前项除以后项的商
把比的前项和后项化成最简整数比
前项 ÷ 后项
运用比的基本性质
是一个数(可以是分数、小数或整数)
仍是一个比
比与分数、除法有什么联系 请大家先填写教材第2题的表格,再说一说它们的区别。
2.比与分数、除法的关系。
名称 各个部分 化简比
分数
除法
比
分子
分数线
分母
分数值
被除数
除号÷
除数
商
4÷2=2
前项
比号:
后项
比值
6:3=2
a÷b=a:b(b≠0)。
你能用字母来表示比与分数、除法之间的关系吗?
想一想,比与分数、除法有什么区别?
比指的是两个数的关系,分数是一个数,除法是一种运算。
3.比的基本性质、分数的基本性质和商不变的规律之间的联系。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
商不变的规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
结合比与分数、除法之间的联系,你能说说比的基本性质、分数的基本性质和商不变的规律之间有什么样的联系吗?
比的前项相当于分数中的分子、除法中的被除数,比号相当于分数中的分数线、除法中的除号,比的后项相当于分数中的分母、除法中的除数,比值相当于分数中的分数值、除法中的商,所以它们的变化规律是一样的。
我们在应用这些性质和规律时,都是将各部分同时乘或除以一个相同的数(0除外),结果不变。
练习:
9:4=4.5:x
x:2.6=3:
x
x=20.8
x=2
x=
练习:
妈妈和面做面条,一共做了1.8 kg,面粉和水的质量比是7:2。面粉和水分别用了多少千克?
1.8×=1.4(kg)
1.8×=0.4(kg)
答:面粉用了1.4 kg,水用了0.4 kg。
练习:
一块金牌重412 g,其中所含的黄金质量与金牌总质量的比为3:206,做302块这样的金牌需要黄金多少克?
412××302=1812(克)
答:做302块这样的金牌需要黄金1812克。
4.正、反比例的意义
发芽率一定,发芽的种子数与种子的总数。
圆柱的侧面积一定,它的底面半径和高。
订阅某报的份数和钱数。
判断下列相关联的两种量是否成比例,成什么比例。
正比例
反比例
正比例
想一想,你是怎么判断相关联的两个量成正比例关系或成反比例关系的呢?
你能用字母来表示正、反比例的意义吗
正比例关系:=k(一定)
反比例关系:xy=k(一定)
说一说正比例和反比例有什么相同点和不同点。
正比例 反比例
相同点 不同点
1.都是描述两种相关联的量。
2.一种量随着另一种量的变化而变化
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
2.相对应的每两个数的比值(商) 是一定的。
3.关系式:=k(一定)
1.变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2.相对应的每两个数的乘积是一定的。
3.关系式:x×y=k(一定)
练习
1.判断下面各题中的两个量是否成正比例或反比例关系。
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知=3,y与x。
(3)三角形的面积一定,它的底与高。
(4)正方体的表面积与它的一个面的面积。
(5)已知xy=1,y与x。
(6)出油率一定,花生油的质量与花生的质量。
不成比例
成正比例
成反比例
成正比例
成反比例
成正比例
已知一辆汽车3小时行135 km,照这样计算,这辆汽车6小时行多少千米
“六一”儿童节,某小学表演大型团体操。原计划站36行,正好每行站24人。后来改站32行,每行能站多少人
比一比,想一想,这两道题有什么不同? 能用比例方法解答吗
用比例方法解决问题的步骤和关键是什么
①根据不变量,判断题中哪两种相关联的量成正比例或反比例。
②找出两组相对应的数,并设出未知数,列出比例。
③解比例。
④检验并写出答语。
在同一幅地图上,量得甲、乙两地的距离是20 cm,甲、丙两地的距离是12 cm。如果甲、乙两地的实际距离是1600 km,那么甲、丙两地的实际距离是多少
解:设甲、丙两地的实际距离是x km 。
20∶1600=12∶x
x=960
答:甲、丙两地的实际距离是960 km。
三、综合应用,提升能力
甲地到乙地的高速公路大约长200 km,乙地到丙地的高速公路大约长280 km。一辆汽车从甲地出发经乙地开往丙地,当行驶到乙地时用了2.5小时。按照这个速度,该车从甲地到丙地大约需要多少小时
280÷(200÷2.5)=3.5(h)
2.5+3.5=6(h)
答:该车从甲地到丙地大约需要6小时。
四、课堂小结
回顾今天的复习过程,你们有什么收获呢?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
