第9章 平行线复习课件

课件34张PPT。§9 平行线复习课回顾与总结1.两直线相交形成几个角,有几对相等的角？
2.平面内的两条直线被第三条直线所截，在形成的8个角中共有几对同位角？有几对内错角？有几对同旁内角？
3.平行线有哪些性质？
4.平行线的判定方法有哪些？
5.什么是两条平行线间的距离？
6.应用所学解决问题1. 互为邻补角:两条直线相交所构成的四了角中,有公共顶点且
有一条公共边的两个角是邻补角。如图(1) 122. 对顶角: (1)两条直线相交所构成的四个角中，(1) 有公共顶点但没有公共边的两个角是对顶角。
如图(2).(2)1234(2)一个角的两边分别是另一个角的两边的反向延长线，这两个角是对顶角。3. 邻补角的性质: 同角的补角相等。
4. 对顶角性质:对顶角相等。两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线。n条直线相交于一点，
就有n(n-1)对对顶角。平行线的性质
1、 两直线平行,同位角相等
2、两直线平行,内错角相等
3、 两直线平行,同旁内角互补返回平行线的判定方法:
1、 同位角相等,两直线平行
2、内错角相等,两直线平行
3、 同旁内角互补,两直线平行 知识梳理返回返回平行线间的距离1.如果两条直线平行，那么其中一条直线上每个点到另一条直线的距离都相等。这个距离，叫做两条平行线间的距离。
2.做距离的方法：
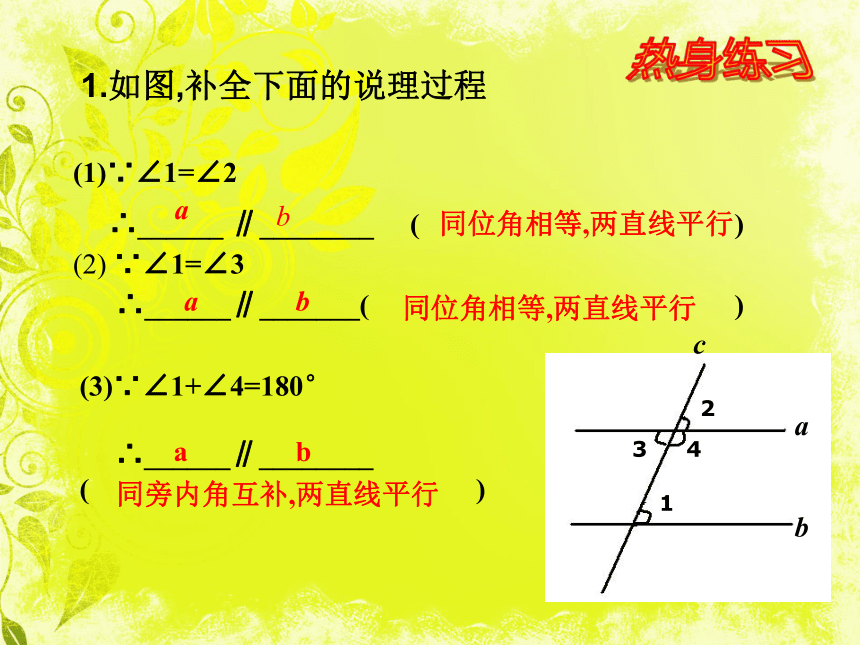
先在一条直线上任取一点，从这一点向另一条直线做垂线，所得垂线段的长度既是平行线间的距离。返回1.如图,补全下面的说理过程热身练习∵∠1=∠2
∴______ ∥________ ( )(2) ∵∠1=∠3
∴______∥_______( )
(3)∵∠1+∠4=180°

∴______∥________
( )
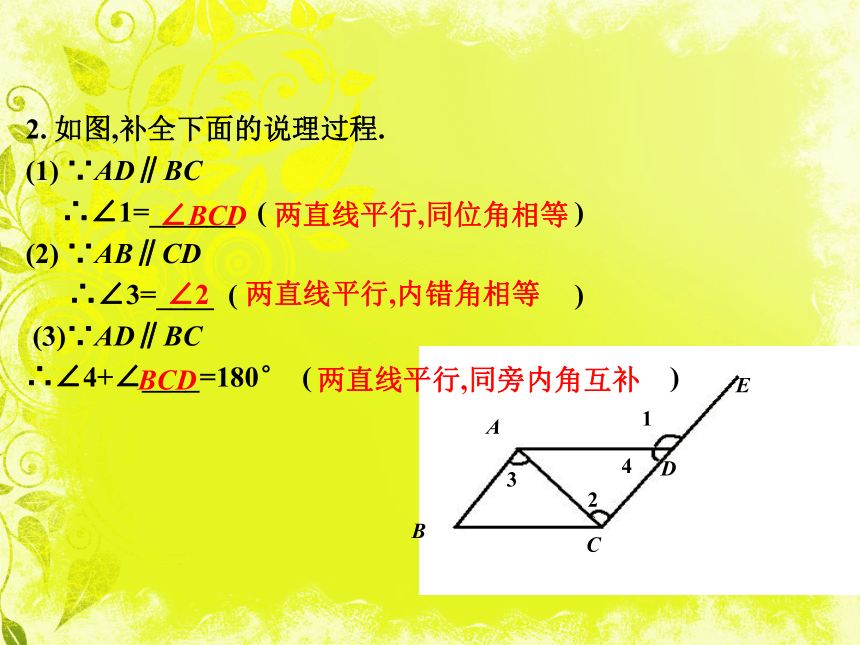
ab同位角相等,两直线平行ab同位角相等,两直线平行ab同旁内角互补,两直线平行2. 如图,补全下面的说理过程.
(1) ∵AD∥BC
∴∠1=______ ( )
(2) ∵AB∥CD
∴∠3=____ ( )
(3)∵AD∥BC
∴∠4+∠____=180° ( )
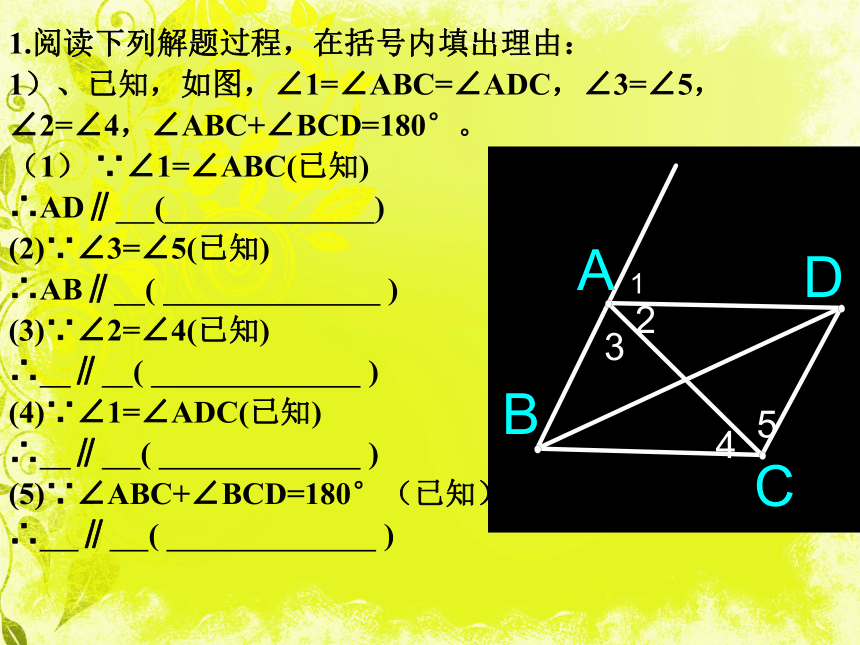
∠BCD∠2BCD两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补1.阅读下列解题过程，在括号内填出理由：
1）、已知，如图，∠1=∠ABC=∠ADC，∠3=∠5，
∠2=∠4，∠ABC+∠BCD=180°。
（1） ∵∠1=∠ABC(已知)
∴AD∥ ( )
(2)∵∠3=∠5(已知)
∴AB∥ ( )
(3)∵∠2=∠4(已知)
∴ ∥ ( )
(4)∵∠1=∠ADC(已知)
∴ ∥ ( )
(5)∵∠ABC+∠BCD=180°（已知）
∴ ∥ ( )
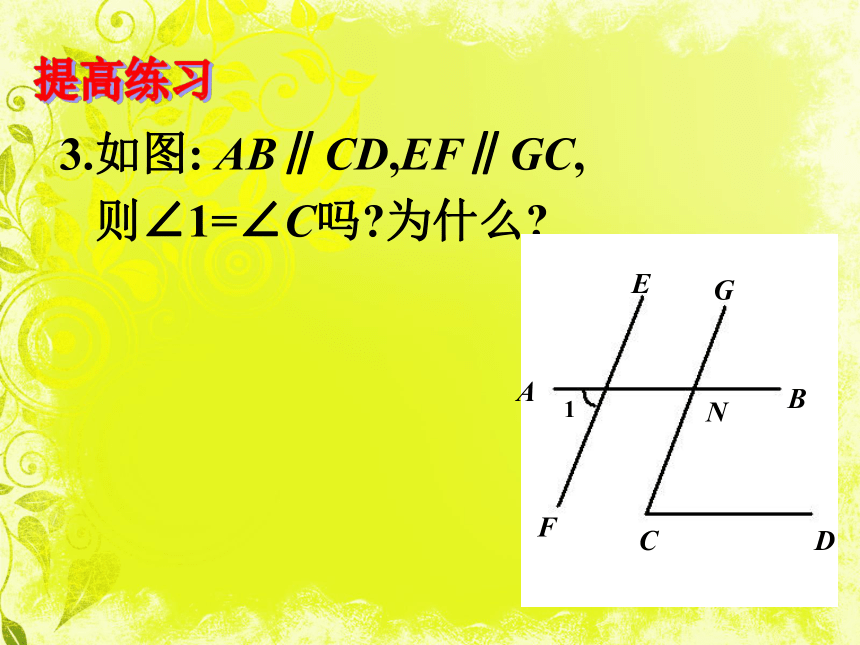
3.如图: AB∥CD,EF∥GC,
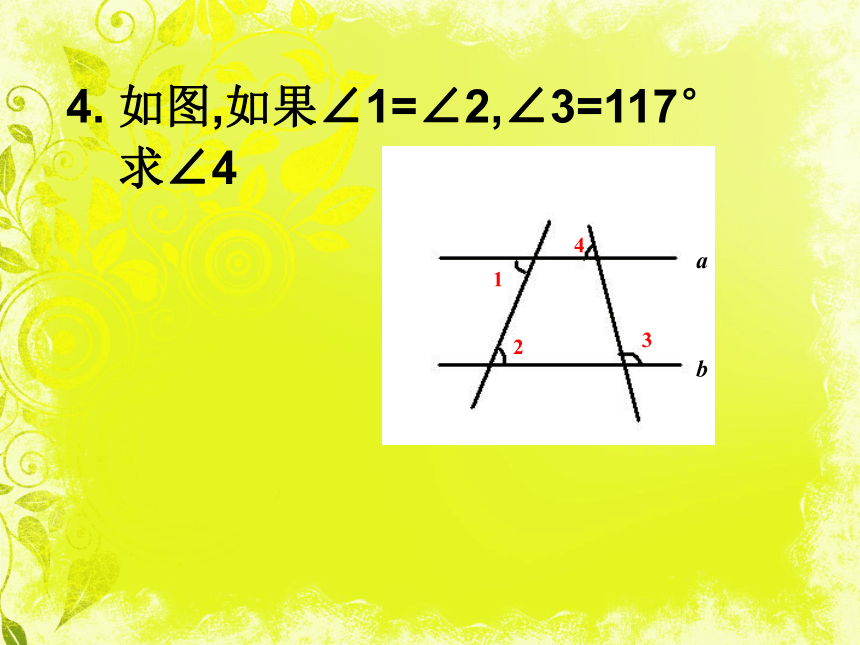
则∠1=∠C吗?为什么?提高练习4. 如图,如果∠1=∠2,∠3=117°
求∠4ABCDO在解
决与角的计算有关
的问题时，经常用
到代数方法。例2.已知直线AB、CD、EF相交于点O，
OABCDEF1.垂线的定义: 两条直线相交，所构成的四个角中，有一个角
是 时，就说这两条直线互相垂直。其中一条直线叫做另一
条直线的垂线。它们的交点叫垂足。2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。
性质(2): 直线外一点与直线上各点连结的所有线段中，垂线
段最短。简称:垂线段最短。3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度，
叫做点到直线的距离。
4.如遇到线段与线段，线段与射线，射线与射线，线段或射线与
直线垂直时，特指它们所在的直线互相垂直。
5.垂线是直线，垂线段特指一条线段是图形，点到直线距离是指
垂线段的长度，是指一个数量，是有单位的。你能量出C到AB的距离,B到AC的距离,A到BC的距离吗? A D C B E F拓 展 应 用 如图：要把水渠中的水引到水池C中，在渠岸的什么地方开沟，水沟的长度才能最短？请画出图来，并说明理由。C∟理由:垂线段最短┓ABCDOE此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。∠1和∠2不是同位角，练 一 练 如图中的∠1和∠2是同位角吗? 为什么?∵∠1和∠2无一边共线。∠1和∠2是同位角，∵∠1和∠2有一边共线、同向且不共顶点。5. 已知BD∥CE, ∠C=∠D
试说明DF∥AC 已知∠1=∠2, ∠C=∠D
试说明DF∥AC 如图，△ABC中，∠B＝∠C。AE平分∠CAD，判断AE与BC是否平行，并说明理由。6．如图，在Ａ，Ｂ两地之间要修一条笔直的公路，从Ｂ测得公路的走向是北偏东５０度，那么从Ａ点测得公路的走向是南偏西多少度？为什么？答：南偏西５０度．因为两直线平行，内错角相等．议一议解答．∵ ∠1= ∠4 ﹙已知﹚ ∴ AB ∥CD﹙同位角相等，两直线平行﹚∴ ∠1 = ∠2 ﹙两直线平行，内错角相等﹚
∠1+ ∠3=180°﹙两直线平行， 同旁内角互补﹚做一做7．若∠１＝ ∠４，那么∠１与∠２相等吗？ ∠１与∠３互补吗？为什么？小试牛刀如图, 若∠3=∠4，则 ∥ ；AD1若AB∥CD, 则∠ =∠ 。
BC2如图，∠D=70°，∠C= 110°,∠1=69°，
则∠B= ·69°3 如图，已知AB∥CD，补充什么条件，能得AD=BC？练一练（1）∠1和 ∠9是由直线 、
被直线 所截成的 角 ； （2）∠6和 ∠12是由直线 、
被直线 所截成的 角 ； （3）∠4和 ∠6是由直线 、
被直线 所截成的 角 ； （4）由直线AB、CD被直线EF 所截成的同位角有 ； （5）∠7和 ∠12是 角 ； ABCDEF同位ABEFCD内错ABCDEF同旁内∠1 和∠9、 ∠4和 ∠12、∠2和∠10、 ∠3 和∠11同旁内5 若两条平行线被第三条直线所截，则一组内错角的平分线互相（ ）
A 垂直 B 平行 C 重合 D 相交4 两条直线被第三条直线所截，则（ ）
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对夹在平行线间的两条线段相等，则两条线段所在的直线的位置关系是（ ）
A 平行 B 相交 C 平行或相交 D不能确定1.两条平行线被第三条直线所截,下列说法错误的是:( )
A.内错角的平分线互相平行
B.同旁内角的平分线互相垂直
C.内错角的平分线互相垂直
D.同位角的平分线互相平行.C例.将一条两边沿互相平行的纸带按如图折叠.设∠1=x度,请用关于x的代数式表示∠a的度数.1a例1. ∠1与哪个角是内错角？
ACBDE12答：∠ EAC答：∠ DAB答：∠ BAC,∠BAE , ∠2 ∠1与哪个角是同旁内角？
∠2与哪个角是内错角? 如图，BD⊥AC，EF⊥AC，D、F分别为垂足，∠1＝∠2，试说明∠ADG ＝∠C 。例3.已知 EF⊥AB，CD⊥AB，∠EFB=∠GDC，求证：∠AGD=∠ACB。
证明： ∵ EF⊥AB，CD⊥AB （已知）
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB＝ ∠DCB
（两直线平行，同位角相等）
∵ ∠EFB=∠GDC （已知）
∴ ∠DCB=∠GDC （等量代换）
∴ DG∥BC （内错角相等,两直线平行）
∴ ∠AGD=∠ACB
（两直线平行，同位角相等）
例2. 已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC 证明: ∵ ∠DAC= ∠ACB (已知)
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=1800(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
ABCDEF例1. 如图 已知：∠1+∠2=180°，求证：AB∥CD。 证明：∵∠1+∠2=180°(已知)
∠1=∠3（对顶角相等）
∠2=∠4（对顶角相等) ∴∠3+∠4=180°(等量代换)
∴AB//CD(同旁内角互补，两直线平行).例2. 如图，已知：AC∥DE，∠1=∠2，试证明AB∥CD。 证明： ∵AC∥DE （已知）
∴ ∠ACD= ∠2 (两直线平行，内错角相等)
∵ ∠1=∠2（已知）
∴ ∠1=∠ACD(等量代换)
∴AB ∥ CD
(内错角相等，两直线平行)