人教版 七年级下册5.3.1 平行线的性质 同步练习 (含解析)
文档属性
| 名称 | 人教版 七年级下册5.3.1 平行线的性质 同步练习 (含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 375.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 10:59:12 | ||
图片预览


文档简介
5.3.1 平行线的性质 同步练习
一、单选题
1.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次向左拐50°,第二次向左拐120°
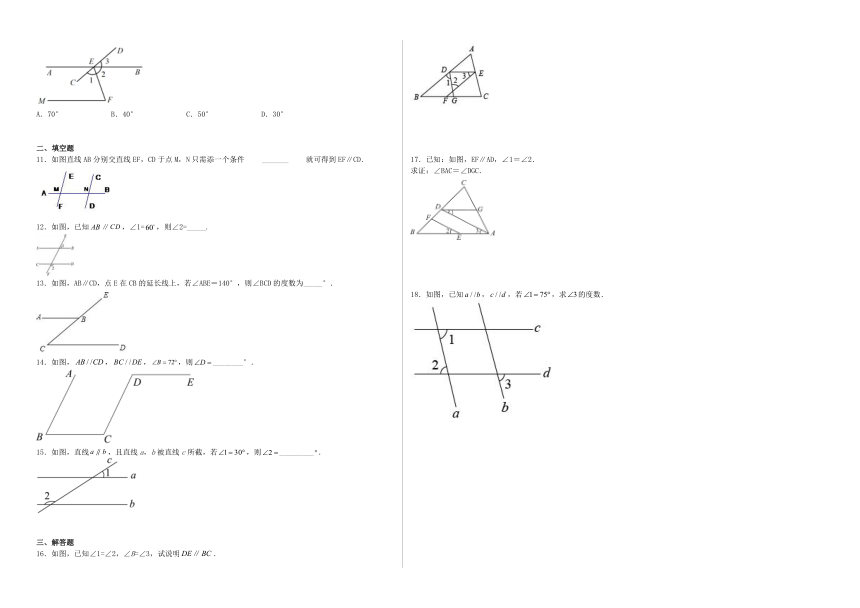
2.一座房屋的屋架结构如图,,要使横梁,则的度数为( )
A.a B. C.2a D.
3.如图所示,直线,且被直线所截, ,,则的度数是( )
A. B. C. D.
4.如图,已知∠1 = 40°,∠2=40°,∠3 = 140°,则∠4的度数等于( )
A.40° B.36° C.44° D.100°
5.如图,已知∠1=110°,∠2=70°,∠4=115°,则∠3的度数为( )
A.65 B.70 C.97 D.115
6.已知:如图,直线a,b被直线c所截,且a//b,若∠1=70°,则∠2的度数是( )
A.110° B.130° C.80° D.70°
7.如图,直线l1∥l2,直线l1、l2被直线l3所截,若∠1=54°,则∠2的大小为( )
A.36° B.46° C.126° D.136°
8.如图,若a∥b,c∥d,∠1=72°,则下列结论错误的是( )
A.∠2=108° B.∠3=72°
C.∠4=108° D.∠5=72°
9.如图,直线ab,∠1=65°,那么∠2的度数是( ).
A.85° B.115° C.125° D.135°
10.如图,直线AB与CD相交于点E,EF平分∠CEB,.若∠F=70°,则∠3=( )
A.70° B.40° C.50° D.30°
二、填空题
11.如图直线AB分别交直线EF,CD于点M,N只需添一个条件 _______ 就可得到EF∥CD.
12.如图,已知∥,∠1=,则∠2=_____.
13.如图,AB∥CD,点E在CB的延长线上,若∠ABE=140°,则∠BCD的度数为_____°.
14.如图,,,,则________°.
15.如图,直线,且直线a,b被直线c所截,若,则_________.
三、解答题
16.如图,已知∠1=∠2,∠B=∠3,试说明.
17.已知:如图,EF∥AD,∠1=∠2.
求证:∠BAC=∠DGC.
18.如图,已知,,若,求的度数.
参考答案
1.A
【详解】如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选A.
2.A
【详解】,
,
,
.
故选A.
3.A
【详解】
,即
解得
故选:A.
4.A
【详解】∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴PQMN,
∴∠4=180°﹣∠3=40°,
故选:A.
5.D
【详解】∵∠2=∠5=70°,∠1=110°,
∴∠1+∠5=180°,
∴a∥b(同旁内角互补两直线平行),
∴∠4=∠3,
∵∠4=115°,
∴∠3=115°.
故选D.
6.A
【详解】∵a//b,
∴∠1=∠3=70°,
∴∠2=180°-∠3=180°-70°=110°,
故选A.
7.C
【详解】解:如图.
∵l1∥l2,
∴∠1=∠3=54°.
∴∠2=180°﹣∠3=180°﹣54°=126°.
故选:C.
8.C
【详解】解:a∥b,c∥d,且∠1=72°,
∠2=180°-∠1=180°-72°=108°,故A不符合题意;
∠3=180°-∠2=180°-108°=72°,故B不符合题意;
∠4=∠3=72°, 故C符合题意;
∠5=∠3=72°,故D不符合题意.
故选C.
9.B
【详解】解:如图所示,∵ab
∴∠3=∠1=65°
∵∠2+∠3=180°
∴∠2=180°-∠3=180°-65°=115°
故选:B.
10.B
【详解】∵EF平分∠CEB
∴∠1=∠2
∵
∴∠F=∠2=70°
∵∠1+∠2+∠3=180°
∴
故选:B.
11.
【详解】试题分析:已知直线AB分别交直线EF,CD于点M,N,要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.如∠AME=∠ANC,利用同位角相等,判定两直线平行.
12.
【详解】如图,
∵AB∥CD,
∴∠1=∠3,
而∠1=60°,
∴∠3=60°,
又∵∠2+∠3=180°,
∴∠2=180°-60°=120°.
故答案是:120°.
13.
【详解】解:∵AB∥CD,
∴∠BCD=∠ABC,
∵∠ABC=180°﹣∠ABE=40°,
∴∠BCD=40°,
故答案为40.
14.
【详解】∵,
.
,
.
,
.
故答案为:108.
15.
【详解】解:如图,
直线,,
,
,
故答案为:.
16.
【详解】解:∵∠1=∠2(已知),
∴(内错角相等,两直线平行),
∴∠B=∠EFC(两直线平行,同位角相等),
∵∠B=∠3(已知),
∴∠3=∠EFC(等量代换),
∴(内错角相等,两直线平行).
17.
【详解】证明:∵EF∥AD,∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.∴DG∥AB.
∴∠BAC=∠DGC.
18.
【详解】解:如图,
∵,
∴∠1=∠4,
∵,
∴∠3=∠4,
∴∠3=∠1,
∵,
∴∠3=75 .
一、单选题
1.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次向左拐50°,第二次向左拐120°
2.一座房屋的屋架结构如图,,要使横梁,则的度数为( )
A.a B. C.2a D.
3.如图所示,直线,且被直线所截, ,,则的度数是( )
A. B. C. D.
4.如图,已知∠1 = 40°,∠2=40°,∠3 = 140°,则∠4的度数等于( )
A.40° B.36° C.44° D.100°
5.如图,已知∠1=110°,∠2=70°,∠4=115°,则∠3的度数为( )
A.65 B.70 C.97 D.115
6.已知:如图,直线a,b被直线c所截,且a//b,若∠1=70°,则∠2的度数是( )
A.110° B.130° C.80° D.70°
7.如图,直线l1∥l2,直线l1、l2被直线l3所截,若∠1=54°,则∠2的大小为( )
A.36° B.46° C.126° D.136°
8.如图,若a∥b,c∥d,∠1=72°,则下列结论错误的是( )
A.∠2=108° B.∠3=72°
C.∠4=108° D.∠5=72°
9.如图,直线ab,∠1=65°,那么∠2的度数是( ).
A.85° B.115° C.125° D.135°
10.如图,直线AB与CD相交于点E,EF平分∠CEB,.若∠F=70°,则∠3=( )
A.70° B.40° C.50° D.30°
二、填空题
11.如图直线AB分别交直线EF,CD于点M,N只需添一个条件 _______ 就可得到EF∥CD.
12.如图,已知∥,∠1=,则∠2=_____.
13.如图,AB∥CD,点E在CB的延长线上,若∠ABE=140°,则∠BCD的度数为_____°.
14.如图,,,,则________°.
15.如图,直线,且直线a,b被直线c所截,若,则_________.
三、解答题
16.如图,已知∠1=∠2,∠B=∠3,试说明.
17.已知:如图,EF∥AD,∠1=∠2.
求证:∠BAC=∠DGC.
18.如图,已知,,若,求的度数.
参考答案
1.A
【详解】如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选A.
2.A
【详解】,
,
,
.
故选A.
3.A
【详解】
,即
解得
故选:A.
4.A
【详解】∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴PQMN,
∴∠4=180°﹣∠3=40°,
故选:A.
5.D
【详解】∵∠2=∠5=70°,∠1=110°,
∴∠1+∠5=180°,
∴a∥b(同旁内角互补两直线平行),
∴∠4=∠3,
∵∠4=115°,
∴∠3=115°.
故选D.
6.A
【详解】∵a//b,
∴∠1=∠3=70°,
∴∠2=180°-∠3=180°-70°=110°,
故选A.
7.C
【详解】解:如图.
∵l1∥l2,
∴∠1=∠3=54°.
∴∠2=180°﹣∠3=180°﹣54°=126°.
故选:C.
8.C
【详解】解:a∥b,c∥d,且∠1=72°,
∠2=180°-∠1=180°-72°=108°,故A不符合题意;
∠3=180°-∠2=180°-108°=72°,故B不符合题意;
∠4=∠3=72°, 故C符合题意;
∠5=∠3=72°,故D不符合题意.
故选C.
9.B
【详解】解:如图所示,∵ab
∴∠3=∠1=65°
∵∠2+∠3=180°
∴∠2=180°-∠3=180°-65°=115°
故选:B.
10.B
【详解】∵EF平分∠CEB
∴∠1=∠2
∵
∴∠F=∠2=70°
∵∠1+∠2+∠3=180°
∴
故选:B.
11.
【详解】试题分析:已知直线AB分别交直线EF,CD于点M,N,要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.如∠AME=∠ANC,利用同位角相等,判定两直线平行.
12.
【详解】如图,
∵AB∥CD,
∴∠1=∠3,
而∠1=60°,
∴∠3=60°,
又∵∠2+∠3=180°,
∴∠2=180°-60°=120°.
故答案是:120°.
13.
【详解】解:∵AB∥CD,
∴∠BCD=∠ABC,
∵∠ABC=180°﹣∠ABE=40°,
∴∠BCD=40°,
故答案为40.
14.
【详解】∵,
.
,
.
,
.
故答案为:108.
15.
【详解】解:如图,
直线,,
,
,
故答案为:.
16.
【详解】解:∵∠1=∠2(已知),
∴(内错角相等,两直线平行),
∴∠B=∠EFC(两直线平行,同位角相等),
∵∠B=∠3(已知),
∴∠3=∠EFC(等量代换),
∴(内错角相等,两直线平行).
17.
【详解】证明:∵EF∥AD,∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.∴DG∥AB.
∴∠BAC=∠DGC.
18.
【详解】解:如图,
∵,
∴∠1=∠4,
∵,
∴∠3=∠4,
∴∠3=∠1,
∵,
∴∠3=75 .
