苏科版八年级下册 第四讲 图形的旋转与中心对称图形 复习讲义(无答案)
文档属性
| 名称 | 苏科版八年级下册 第四讲 图形的旋转与中心对称图形 复习讲义(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 968.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 10:44:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第四讲 图形的旋转与中心对称图形
一 知识点梳理
知识点一、 旋转的概念
1.定义:将一个图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.定点称为旋转中心,旋转的角度称为旋转角.
2.旋转的性质
一个图形和它经过旋转所得到的图形中:
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心连线所成的角相等.
3.旋转的作图
在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键点沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.
知识点二、中心对称和中心对称图形
1.中心对称: 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.
2.中心对称图形: 把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
3.中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区别 ①指两个全等图形之间的相互位置关系.
②对称中心不定. ①指一个图形本身成中心对称.
②对称中心是图形自身或内部的点.
联系 如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形. 如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.
知识点三、中心对称、轴对称、旋转对称
1.中心对称图形与旋转对称图形的比较:
2.中心对称图形与轴对称图形比较:
要点诠释:中心对称图形是特殊的旋转对称图形;掌握三种图形的不同点和共同点是灵活运用的前提.
二 例题讲解
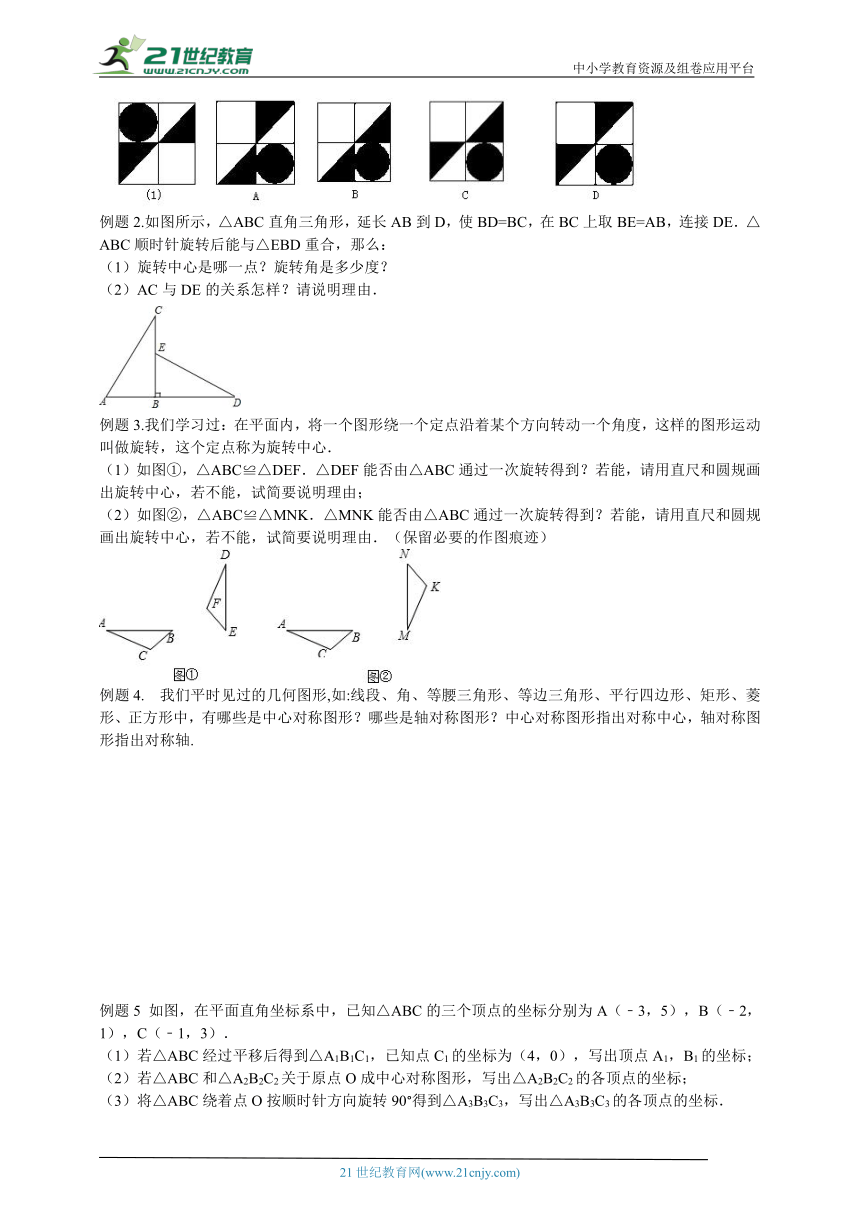
例题1. 如图,将图(1)中的正方形图案绕中心旋转180°后,得到的图案是( )
例题2.如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
例题3.我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心.
(1)如图①,△ABC≌△DEF.△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由;
(2)如图②,△ABC≌△MNK.△MNK能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.(保留必要的作图痕迹)
例题4. 我们平时见过的几何图形,如:线段、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形中,有哪些是中心对称图形?哪些是轴对称图形?中心对称图形指出对称中心,轴对称图形指出对称轴.
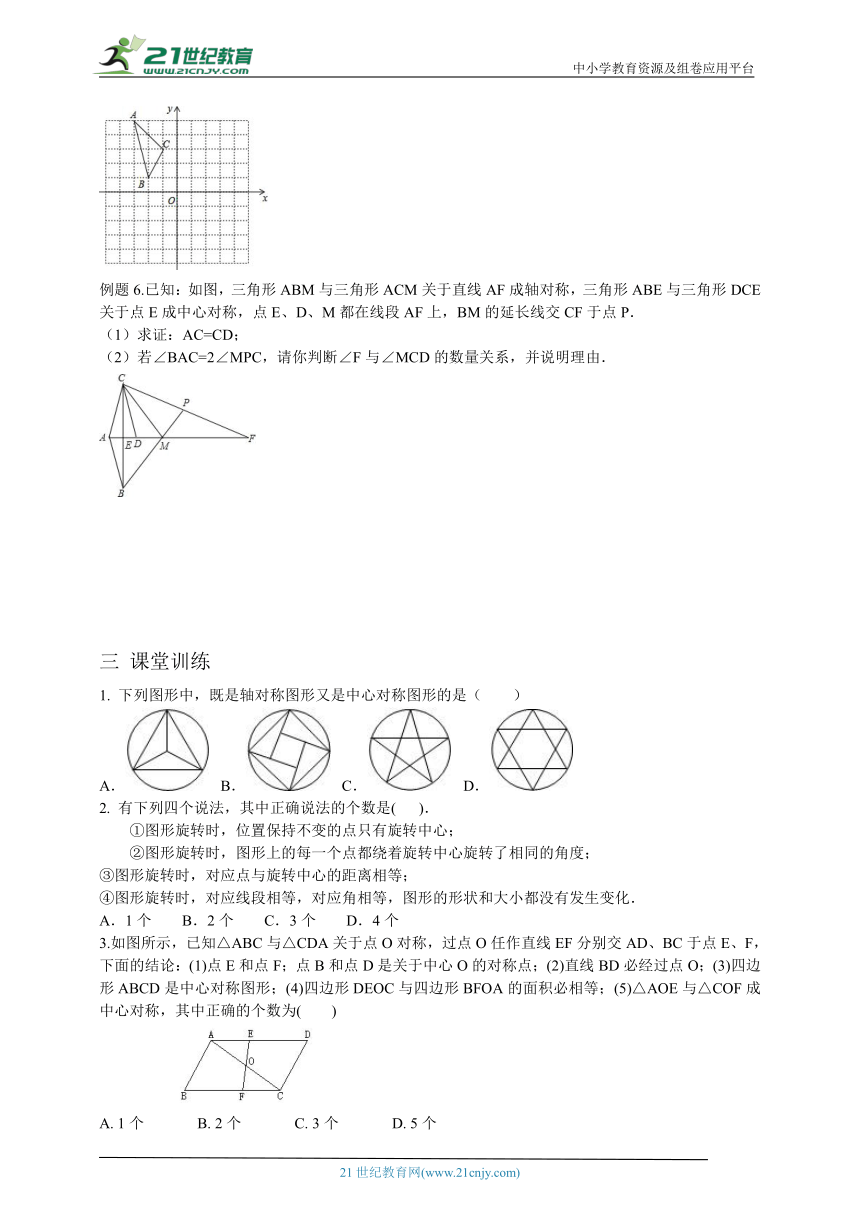
例题5 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
例题6.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
三 课堂训练
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2. 有下列四个说法,其中正确说法的个数是( ).
①图形旋转时,位置保持不变的点只有旋转中心;
②图形旋转时,图形上的每一个点都绕着旋转中心旋转了相同的角度;
③图形旋转时,对应点与旋转中心的距离相等;
④图形旋转时,对应线段相等,对应角相等,图形的形状和大小都没有发生变化.
A.1个 B.2个 C.3个 D.4个
3.如图所示,已知△ABC与△CDA关于点O对称,过点O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;点B和点D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 5个
4.如图,画出绕点逆时针旋转所得到的图形.
5.如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:
①∠BAC=∠B1A1C1;②AC=A1C1; ③OA=OA1;
④△ABC与△A1B1C1的面积相等,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).
四 举一反三
一、选择题
1. 下图中,不是旋转对称图形的是( ).
2.如图,△ADE绕点D的顺时针旋转,旋转的角是∠ADE,得到△CDB,那么下列说法错误的是( ).
A.DE平分∠ADB B.AD=DC C.AE∥BD D.AE=BC
3.下列说法正确的是( )
A.两个会重合的三角形一定成轴对称
B.两个会重合的三角形一定成中心对称
C.成轴对称的两个图形中,对称线段平行且相等
D.成中心对称的两个图形中,对称线段平行(或在同一条直线上)且相等
4.在下列四种图形变换中,本题图案不包含的变换是( )
①中心对称 ②旋转 ③轴对称 ④平移
A.①② B.②③ C.③④ D.①④
5.如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
A.30° B.35° C.40° D.45°
二、 填空题
6.针表的分针匀速旋转一周需要60分钟,则经过15分钟,分针旋转了__________度.
7. 如图,若将△ABC绕点O顺时针旋转180°后得到△,则A点的对应点点的坐标是________.
8.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
9.如图所示,△ABC中,∠BAC=120°,∠DAE=60°,AB=AC,△AEC绕点A旋转到△AFB的位置;∠FAD=__________,∠FBD=__________.
10. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为_____,∠APB=_______°.
三、解答题
11.在如图的正方形网格中,有一个格点三角形ABC(即三角形的顶点都在格点上).
(1)在图中作出三角形ABC关于直线l对称的三角形A1B1C1;
(2)作出三角形ABC的格点P按逆时针方向旋转90°后得到的三角形A2B2C2.
12.阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是 .
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是 .(结果可以不化简)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第四讲 图形的旋转与中心对称图形
一 知识点梳理
知识点一、 旋转的概念
1.定义:将一个图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.定点称为旋转中心,旋转的角度称为旋转角.
2.旋转的性质
一个图形和它经过旋转所得到的图形中:
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心连线所成的角相等.
3.旋转的作图
在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键点沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.
知识点二、中心对称和中心对称图形
1.中心对称: 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.
2.中心对称图形: 把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
3.中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区别 ①指两个全等图形之间的相互位置关系.
②对称中心不定. ①指一个图形本身成中心对称.
②对称中心是图形自身或内部的点.
联系 如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形. 如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.
知识点三、中心对称、轴对称、旋转对称
1.中心对称图形与旋转对称图形的比较:
2.中心对称图形与轴对称图形比较:
要点诠释:中心对称图形是特殊的旋转对称图形;掌握三种图形的不同点和共同点是灵活运用的前提.
二 例题讲解
例题1. 如图,将图(1)中的正方形图案绕中心旋转180°后,得到的图案是( )
例题2.如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
例题3.我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心.
(1)如图①,△ABC≌△DEF.△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由;
(2)如图②,△ABC≌△MNK.△MNK能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.(保留必要的作图痕迹)
例题4. 我们平时见过的几何图形,如:线段、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形中,有哪些是中心对称图形?哪些是轴对称图形?中心对称图形指出对称中心,轴对称图形指出对称轴.
例题5 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
例题6.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
三 课堂训练
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2. 有下列四个说法,其中正确说法的个数是( ).
①图形旋转时,位置保持不变的点只有旋转中心;
②图形旋转时,图形上的每一个点都绕着旋转中心旋转了相同的角度;
③图形旋转时,对应点与旋转中心的距离相等;
④图形旋转时,对应线段相等,对应角相等,图形的形状和大小都没有发生变化.
A.1个 B.2个 C.3个 D.4个
3.如图所示,已知△ABC与△CDA关于点O对称,过点O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;点B和点D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 5个
4.如图,画出绕点逆时针旋转所得到的图形.
5.如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:
①∠BAC=∠B1A1C1;②AC=A1C1; ③OA=OA1;
④△ABC与△A1B1C1的面积相等,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).
四 举一反三
一、选择题
1. 下图中,不是旋转对称图形的是( ).
2.如图,△ADE绕点D的顺时针旋转,旋转的角是∠ADE,得到△CDB,那么下列说法错误的是( ).
A.DE平分∠ADB B.AD=DC C.AE∥BD D.AE=BC
3.下列说法正确的是( )
A.两个会重合的三角形一定成轴对称
B.两个会重合的三角形一定成中心对称
C.成轴对称的两个图形中,对称线段平行且相等
D.成中心对称的两个图形中,对称线段平行(或在同一条直线上)且相等
4.在下列四种图形变换中,本题图案不包含的变换是( )
①中心对称 ②旋转 ③轴对称 ④平移
A.①② B.②③ C.③④ D.①④
5.如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
A.30° B.35° C.40° D.45°
二、 填空题
6.针表的分针匀速旋转一周需要60分钟,则经过15分钟,分针旋转了__________度.
7. 如图,若将△ABC绕点O顺时针旋转180°后得到△,则A点的对应点点的坐标是________.
8.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
9.如图所示,△ABC中,∠BAC=120°,∠DAE=60°,AB=AC,△AEC绕点A旋转到△AFB的位置;∠FAD=__________,∠FBD=__________.
10. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为_____,∠APB=_______°.
三、解答题
11.在如图的正方形网格中,有一个格点三角形ABC(即三角形的顶点都在格点上).
(1)在图中作出三角形ABC关于直线l对称的三角形A1B1C1;
(2)作出三角形ABC的格点P按逆时针方向旋转90°后得到的三角形A2B2C2.
12.阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是 .
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是 .(结果可以不化简)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
