苏科版九年级下册 第3讲:与圆相关的位置关系及计算 复习讲义(无答案)
文档属性
| 名称 | 苏科版九年级下册 第3讲:与圆相关的位置关系及计算 复习讲义(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 333.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 11:13:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第3讲:与圆相关的位置关系及计算
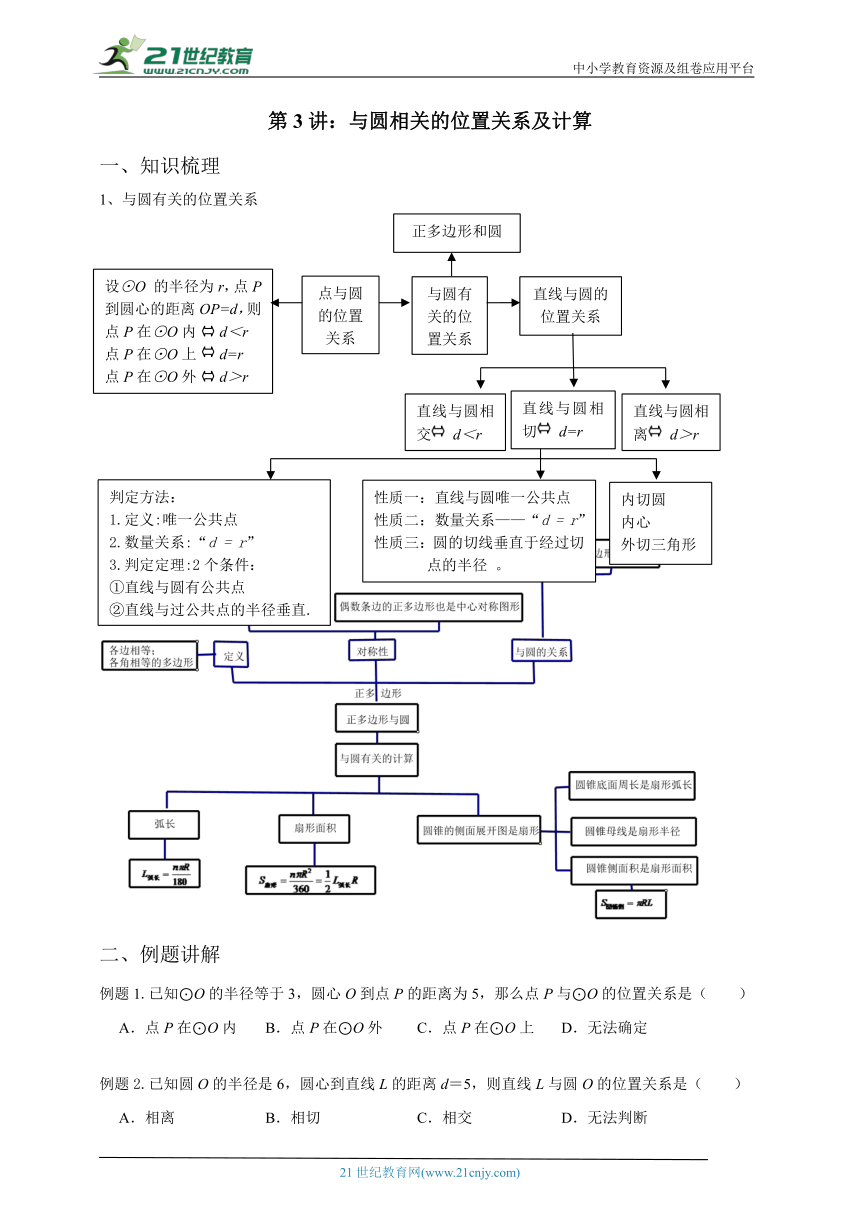
一、知识梳理
1、与圆有关的位置关系
2、与圆有关的计算
二、例题讲解
例题1.已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
例题2.已知圆O的半径是6,圆心到直线L的距离d=5,则直线L与圆O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
例题3.如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作DE⊥AP交AP于E点.
(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
例题4.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
例题5.如图,已知等边△ABC的内切圆⊙O半径为3,则AB的长为( )
A.3 B.3 C.6 D.6
例题6.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A. B. C. D.
例题7.如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,4)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为( )
A.8π B.π C.2π D.48π
例题8.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2 B.100πcm2 C.100πcm2 D.50πcm2
三、课堂训练
1.半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,4)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
2.已知⊙O的半径是10,圆心O到直线l的距离是13,则直线l与⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
3.已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
4.如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连接AD并延长,与BC相交于点E.
(1)若BC=,CD=1,求⊙O的半径;
(2)取BE的中点F,连接DF,求证:DF是⊙O的切线.
5.如图,△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为( )
A.100° B.160° C.80° D.130°
6.如图,菱形OABC的边长为4,且点A、B、C在⊙O上,则劣弧的长度为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ABC=90°,以BC的中点O为圆心,OB的长为半径作半圆交AC于点D,若AD=1,DC=3,则图中阴影部分的面积为( )
A. B. C. D.3π﹣2
8.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是( )
A.30π B.48π C.60π D.80π
四、举一反三
1.圆的直径为10cm,如果点P到圆心O的距离是d,则( )
A.当d=8cm时,点P在⊙O内 B.当d=10cm时,点P在⊙O上
C.当d=5cm时,点P在⊙O上 D.当d=6cm时,点P在⊙O内
2.已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.以上都不对
3.如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,,求AD的长.
4.如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=2,AD=2,求线段BC的长.
5.如图,在△ABC中,∠C=58°,点O为△ABC的内心,则∠AOB的度数为( )
A.119° B.120° C.121° D.122°
6.如图,⊙O的半径为5,AB为弦,若∠ABC=30°,则的长为( )
A.5 B.π C. D.π
7.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,且∠BCD=30°,CD=4.则图中阴影部分的面积S阴影=( )
A.2π B.π C.π D.π
8.若圆锥的母线长为4,底面圆的半径为3,那么该圆锥的高是( )
A.1 B. C.5 D.7
正多边形和圆
点与圆的位置关系
设⊙O 的半径为r,点P到圆心的距离OP=d,则
点P在⊙O内 d<r
点P在⊙O上 d=r
点P在⊙O外 d>r
与圆有关的位置关系
直线与圆的位置关系
直线与圆相交 d<r
直线与圆相切 d=r
直线与圆相离 d>r
判定方法:
1.定义:唯一公共点
2.数量关系:“d = r”
3.判定定理:2个条件:
①直线与圆有公共点
②直线与过公共点的半径垂直.
性质一:直线与圆唯一公共点
性质二:数量关系——“d = r”
性质三:圆的切线垂直于经过切点的半径 。
内切圆
内心
外切三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第3讲:与圆相关的位置关系及计算
一、知识梳理
1、与圆有关的位置关系
2、与圆有关的计算
二、例题讲解
例题1.已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
例题2.已知圆O的半径是6,圆心到直线L的距离d=5,则直线L与圆O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
例题3.如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作DE⊥AP交AP于E点.
(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
例题4.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
例题5.如图,已知等边△ABC的内切圆⊙O半径为3,则AB的长为( )
A.3 B.3 C.6 D.6
例题6.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A. B. C. D.
例题7.如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,4)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为( )
A.8π B.π C.2π D.48π
例题8.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2 B.100πcm2 C.100πcm2 D.50πcm2
三、课堂训练
1.半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,4)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
2.已知⊙O的半径是10,圆心O到直线l的距离是13,则直线l与⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
3.已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
4.如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连接AD并延长,与BC相交于点E.
(1)若BC=,CD=1,求⊙O的半径;
(2)取BE的中点F,连接DF,求证:DF是⊙O的切线.
5.如图,△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为( )
A.100° B.160° C.80° D.130°
6.如图,菱形OABC的边长为4,且点A、B、C在⊙O上,则劣弧的长度为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ABC=90°,以BC的中点O为圆心,OB的长为半径作半圆交AC于点D,若AD=1,DC=3,则图中阴影部分的面积为( )
A. B. C. D.3π﹣2
8.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是( )
A.30π B.48π C.60π D.80π
四、举一反三
1.圆的直径为10cm,如果点P到圆心O的距离是d,则( )
A.当d=8cm时,点P在⊙O内 B.当d=10cm时,点P在⊙O上
C.当d=5cm时,点P在⊙O上 D.当d=6cm时,点P在⊙O内
2.已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.以上都不对
3.如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,,求AD的长.
4.如图,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=2,AD=2,求线段BC的长.
5.如图,在△ABC中,∠C=58°,点O为△ABC的内心,则∠AOB的度数为( )
A.119° B.120° C.121° D.122°
6.如图,⊙O的半径为5,AB为弦,若∠ABC=30°,则的长为( )
A.5 B.π C. D.π
7.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,且∠BCD=30°,CD=4.则图中阴影部分的面积S阴影=( )
A.2π B.π C.π D.π
8.若圆锥的母线长为4,底面圆的半径为3,那么该圆锥的高是( )
A.1 B. C.5 D.7
正多边形和圆
点与圆的位置关系
设⊙O 的半径为r,点P到圆心的距离OP=d,则
点P在⊙O内 d<r
点P在⊙O上 d=r
点P在⊙O外 d>r
与圆有关的位置关系
直线与圆的位置关系
直线与圆相交 d<r
直线与圆相切 d=r
直线与圆相离 d>r
判定方法:
1.定义:唯一公共点
2.数量关系:“d = r”
3.判定定理:2个条件:
①直线与圆有公共点
②直线与过公共点的半径垂直.
性质一:直线与圆唯一公共点
性质二:数量关系——“d = r”
性质三:圆的切线垂直于经过切点的半径 。
内切圆
内心
外切三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
