苏科版九年级下册 第1讲:多边形与特殊四边形 复习讲义(无答案)
文档属性
| 名称 | 苏科版九年级下册 第1讲:多边形与特殊四边形 复习讲义(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 466.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 11:13:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第1讲:多边形与特殊四边形
一、知识梳理
1、平行四边形
2、矩形
3、菱形
4、正方形
二、例题讲解
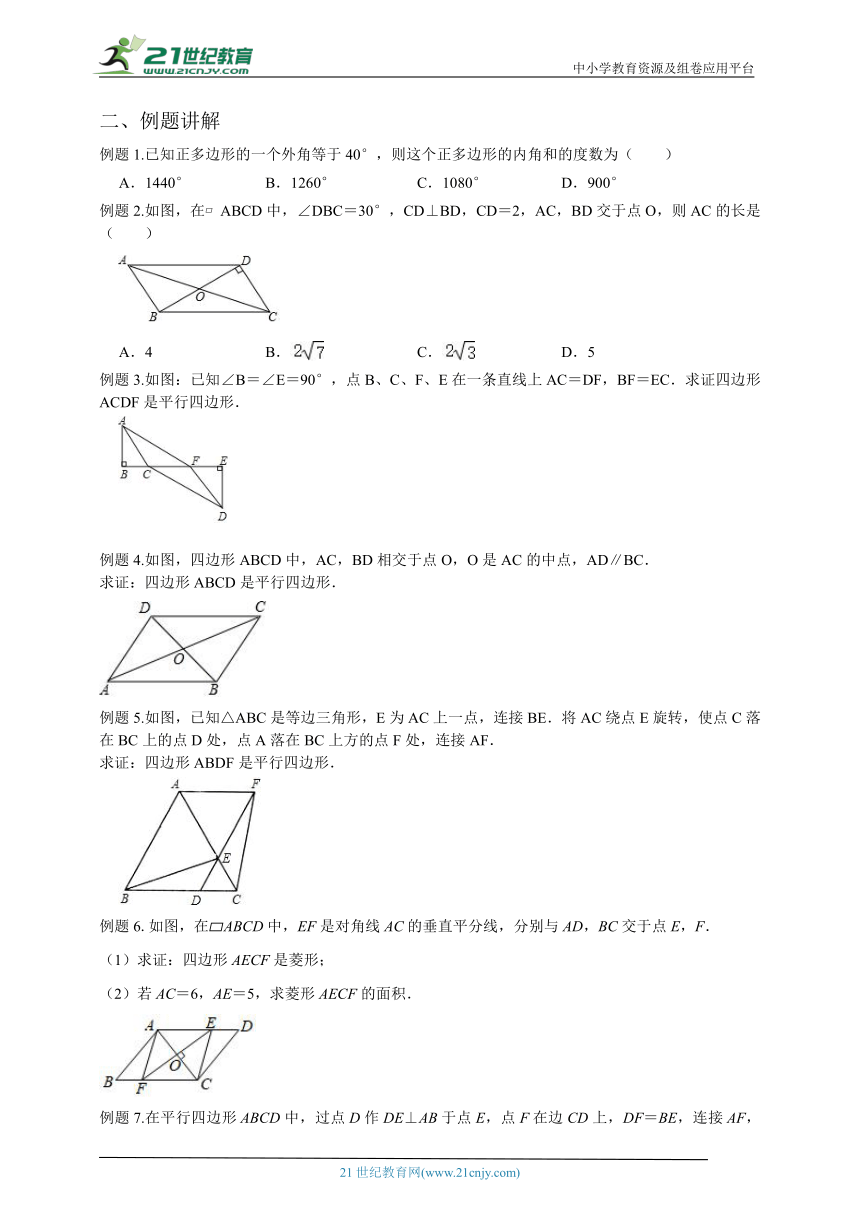
例题1.已知正多边形的一个外角等于40°,则这个正多边形的内角和的度数为( )
A.1440° B.1260° C.1080° D.900°
例题2.如图,在 ABCD中,∠DBC=30°,CD⊥BD,CD=2,AC,BD交于点O,则AC的长是( )
A.4 B. C. D.5
例题3.如图:已知∠B=∠E=90°,点B、C、F、E在一条直线上AC=DF,BF=EC.求证四边形ACDF是平行四边形.
例题4.如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
求证:四边形ABCD是平行四边形.
例题5.如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.
求证:四边形ABDF是平行四边形.
例题6.如图,在 ABCD中,EF是对角线AC的垂直平分线,分别与AD,BC交于点E,F.
(1)求证:四边形AECF是菱形;
(2)若AC=6,AE=5,求菱形AECF的面积.
例题7.在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,tanC=,DC=16,求证:AF平分∠DAB.
例题8.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.
(1)求证:四边形ABCD是正方形;
(2)连结BD,交EF于点Q,求证:DQ BC=CE DF.
三、课堂训练
1.若一个正多边形的外角等于其内角,则这个正多边形的边数为( )
A.3 B.4 C.5 D.6
2.如图,将平行四边形ABCD的一边BC延长至点E,若∠A=125°,则∠1=( )
A.125° B.65° C.55° D.45°
3.已知:如图,A,B,C,D在同一直线上,且AB=CD,AE=DF,AE∥DF.求证:四边形EBFC是平行四边形.
4.如图,点B、E、C、F在一条直线上,AB∥DF,AC∥DE,BE=FC,连接BD、AF.求证:四边形ABDF是平行四边形.
5.如图,Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,点F在BC的延长线上,且∠CEF=∠A;求证:四边形DCFE为平行四边形.
6.如图,在平行四边形ABCD中,AE⊥BC,AF⊥DC,垂足分别为E,F,且BE=DF.
(1)求证:平行四边形ABCD是菱形;
(2)若AB=5,AC=6,求四边形ABCD的面积.
7.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=1,求△OEC的面积.
8.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
四、举一反三
1.一个正多边形的内角和比外角和多360°,则该正多边形的边数是( )
A.5 B.6 C.7 D.8
2.平面直角坐标系中,已知平行四边形ABCD的三个顶点的坐标分别是A(m,n),B(1,﹣3),C(﹣m,﹣n),则点D的坐标是( )
A.(1,﹣3) B.(﹣1,﹣3) C.(﹣1,3) D.(1,3)
3.如图,AB∥CD,AB=CD,BF⊥AC于点F,DE⊥AC于点E求证:四边形DEBF是平行四边形.
4.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形
(2)求四边形ACEB的周长.
5.如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC上,EF=EC.求证:四边形DBFE是平行四边形.
6.如图,在△ABC中,若∠BAC=90°,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,过点C作CG∥AD交BA延长线于G,过点A作AH∥BC交CG于H.
(1)求证:四边形ADCH是菱形;
(2)若DE=6,求四边形ACDE的面积.
7.如图,BD为 ABCD的对角线,BD⊥AD,延长AD到点E,使得DE=AD,连接CE.
(1)求证:四边形BCED是矩形;
(2)若四边形BCED的周长是6,AB=5,求四边形BCED的面积.
8.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
对角线
边
菱形
定义
平行四
边形
性质
判定
对称性
角
面积
边
对角线
对角线
边
菱形
定义
平行四
边形
性质
判定
对称性
角
面积
边
对角线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第1讲:多边形与特殊四边形
一、知识梳理
1、平行四边形
2、矩形
3、菱形
4、正方形
二、例题讲解
例题1.已知正多边形的一个外角等于40°,则这个正多边形的内角和的度数为( )
A.1440° B.1260° C.1080° D.900°
例题2.如图,在 ABCD中,∠DBC=30°,CD⊥BD,CD=2,AC,BD交于点O,则AC的长是( )
A.4 B. C. D.5
例题3.如图:已知∠B=∠E=90°,点B、C、F、E在一条直线上AC=DF,BF=EC.求证四边形ACDF是平行四边形.
例题4.如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
求证:四边形ABCD是平行四边形.
例题5.如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.
求证:四边形ABDF是平行四边形.
例题6.如图,在 ABCD中,EF是对角线AC的垂直平分线,分别与AD,BC交于点E,F.
(1)求证:四边形AECF是菱形;
(2)若AC=6,AE=5,求菱形AECF的面积.
例题7.在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,tanC=,DC=16,求证:AF平分∠DAB.
例题8.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.
(1)求证:四边形ABCD是正方形;
(2)连结BD,交EF于点Q,求证:DQ BC=CE DF.
三、课堂训练
1.若一个正多边形的外角等于其内角,则这个正多边形的边数为( )
A.3 B.4 C.5 D.6
2.如图,将平行四边形ABCD的一边BC延长至点E,若∠A=125°,则∠1=( )
A.125° B.65° C.55° D.45°
3.已知:如图,A,B,C,D在同一直线上,且AB=CD,AE=DF,AE∥DF.求证:四边形EBFC是平行四边形.
4.如图,点B、E、C、F在一条直线上,AB∥DF,AC∥DE,BE=FC,连接BD、AF.求证:四边形ABDF是平行四边形.
5.如图,Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,点F在BC的延长线上,且∠CEF=∠A;求证:四边形DCFE为平行四边形.
6.如图,在平行四边形ABCD中,AE⊥BC,AF⊥DC,垂足分别为E,F,且BE=DF.
(1)求证:平行四边形ABCD是菱形;
(2)若AB=5,AC=6,求四边形ABCD的面积.
7.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=1,求△OEC的面积.
8.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
四、举一反三
1.一个正多边形的内角和比外角和多360°,则该正多边形的边数是( )
A.5 B.6 C.7 D.8
2.平面直角坐标系中,已知平行四边形ABCD的三个顶点的坐标分别是A(m,n),B(1,﹣3),C(﹣m,﹣n),则点D的坐标是( )
A.(1,﹣3) B.(﹣1,﹣3) C.(﹣1,3) D.(1,3)
3.如图,AB∥CD,AB=CD,BF⊥AC于点F,DE⊥AC于点E求证:四边形DEBF是平行四边形.
4.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形
(2)求四边形ACEB的周长.
5.如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC上,EF=EC.求证:四边形DBFE是平行四边形.
6.如图,在△ABC中,若∠BAC=90°,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F,过点C作CG∥AD交BA延长线于G,过点A作AH∥BC交CG于H.
(1)求证:四边形ADCH是菱形;
(2)若DE=6,求四边形ACDE的面积.
7.如图,BD为 ABCD的对角线,BD⊥AD,延长AD到点E,使得DE=AD,连接CE.
(1)求证:四边形BCED是矩形;
(2)若四边形BCED的周长是6,AB=5,求四边形BCED的面积.
8.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
对角线
边
菱形
定义
平行四
边形
性质
判定
对称性
角
面积
边
对角线
对角线
边
菱形
定义
平行四
边形
性质
判定
对称性
角
面积
边
对角线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
