苏科版九年级下册 第12讲:相似与全等之手拉手 复习讲义(无答案)
文档属性
| 名称 | 苏科版九年级下册 第12讲:相似与全等之手拉手 复习讲义(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 11:13:32 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第12讲:相似与全等之手拉手
一、知识梳理
手拉手模型又称共顶点模型,一般指由两个全等图形或相似图形进行旋转可以得到对应的全等三角形或相似三角形。深刻了解,灵活运用此模型可以帮助我们解决很多几何大题。
例题讲解
例题1.如图①,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.则易知四边形CEGF是正方形.
(1)请直接写出的值为 ;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图②所示,(1)中的结论还成立吗?若成立,请给出证明:若不成立,请说明理由.
(3)拓展与运用
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图③所示,延长CG交AD于点H.若AH=,GH=,则BC= .
例题2.【感知】如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
【探究】如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
【应用】如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
三、课堂训练
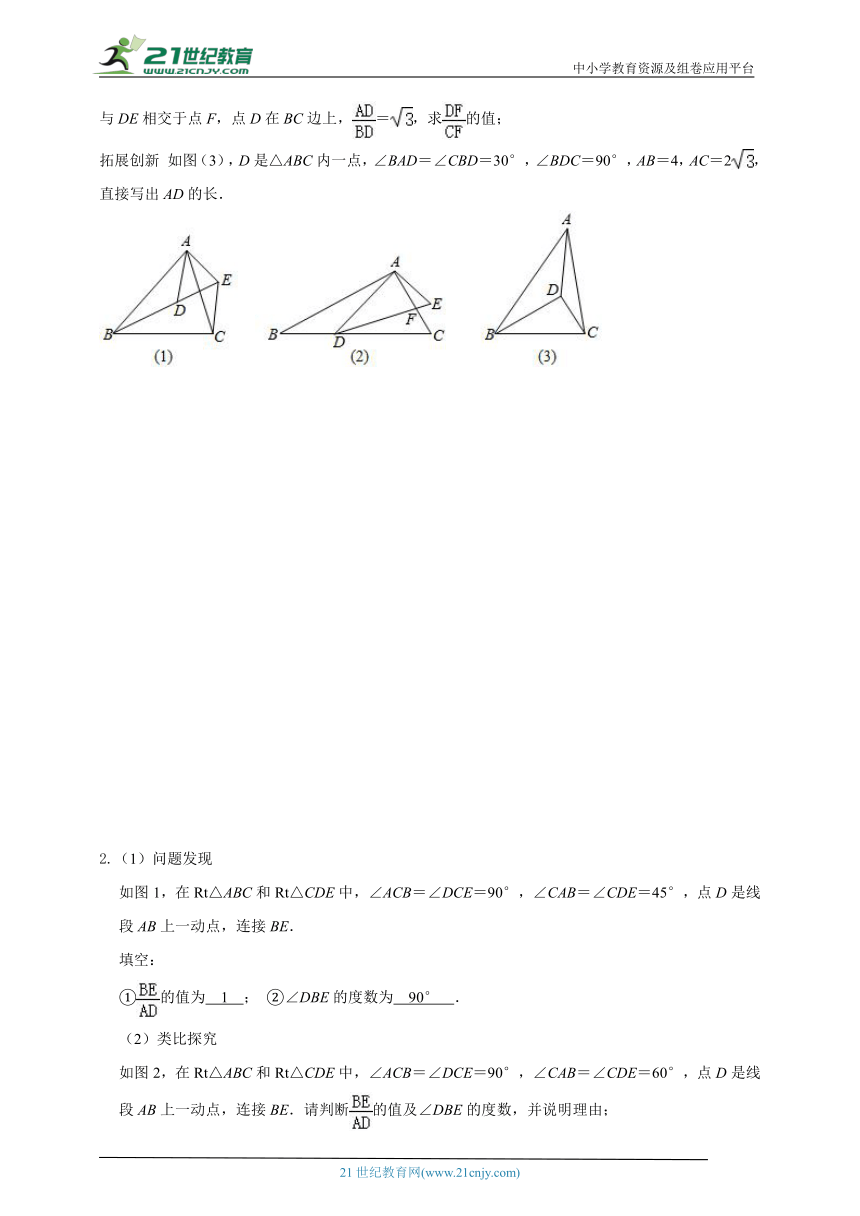
1.问题背景 如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;
尝试应用 如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,求的值;
拓展创新 如图(3),D是△ABC内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB=4,AC=2,直接写出AD的长.
2.(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
填空:
①的值为 1 ; ②∠DBE的度数为 90° .
(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;
(3)拓展延伸
如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.
四、举一反三
1.【操作发现】
(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将ABC绕点A顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,此时∠ABB′= ;
【问题解决】
在某次数学兴趣小组活动中,小明同学遇到了如下问题:
(2)如图2,在等边△ABC中,点P在内部,且PA=3,PC=4,∠APC=150°,求PB的长.
经过同学们的观察、分析、思考、交流、对上述问题形成了如下想法:将△APC绕点A按顺时针方向旋转60°,得到△ABP’,连接PP′,寻找PA、PB、PC三边之间的数量关系……请参考他们的想法,完成该问题的解答过程;
【学以致用】
(3)如图3,在等边△ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°.求△APC的面积;
【思维拓展】
如图4,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),请直接写出BD的长(用含k的式子表示).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第12讲:相似与全等之手拉手
一、知识梳理
手拉手模型又称共顶点模型,一般指由两个全等图形或相似图形进行旋转可以得到对应的全等三角形或相似三角形。深刻了解,灵活运用此模型可以帮助我们解决很多几何大题。
例题讲解
例题1.如图①,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.则易知四边形CEGF是正方形.
(1)请直接写出的值为 ;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图②所示,(1)中的结论还成立吗?若成立,请给出证明:若不成立,请说明理由.
(3)拓展与运用
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图③所示,延长CG交AD于点H.若AH=,GH=,则BC= .
例题2.【感知】如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
【探究】如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
【应用】如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
三、课堂训练
1.问题背景 如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;
尝试应用 如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,求的值;
拓展创新 如图(3),D是△ABC内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB=4,AC=2,直接写出AD的长.
2.(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
填空:
①的值为 1 ; ②∠DBE的度数为 90° .
(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;
(3)拓展延伸
如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.
四、举一反三
1.【操作发现】
(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将ABC绕点A顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,此时∠ABB′= ;
【问题解决】
在某次数学兴趣小组活动中,小明同学遇到了如下问题:
(2)如图2,在等边△ABC中,点P在内部,且PA=3,PC=4,∠APC=150°,求PB的长.
经过同学们的观察、分析、思考、交流、对上述问题形成了如下想法:将△APC绕点A按顺时针方向旋转60°,得到△ABP’,连接PP′,寻找PA、PB、PC三边之间的数量关系……请参考他们的想法,完成该问题的解答过程;
【学以致用】
(3)如图3,在等边△ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°.求△APC的面积;
【思维拓展】
如图4,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),请直接写出BD的长(用含k的式子表示).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
