19.1.2函数的图象(2) 课件(共29张PPT)
文档属性
| 名称 | 19.1.2函数的图象(2) 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 15:48:55 | ||
图片预览





文档简介
(共29张PPT)
19.1.2函数的图象(2)
人教版八年级下册
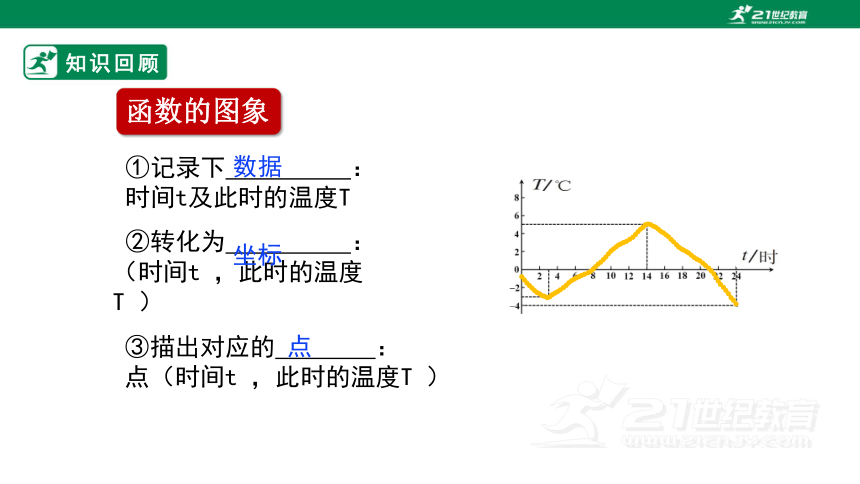
知识回顾
①记录下 :
时间t及此时的温度T
②转化为 :
(时间t ,此时的温度T )
③描出对应的 :
点(时间t ,此时的温度T )
函数的图象
数据
坐标
点
教学目标
1.掌握画函数图象的一般步骤,能画出一些简单的函数图象;
2.能解决相关函数图象问题。
新知导入
通过上节课的学习,我们知道了
函数图象就是把自变量与函数的每对对应值分别作为点的 坐标,在平面直角坐标系内由这些点组成的图形.
横、纵
新知探究
正方形的面积y是边长x的函数,请画出这个函数的图象.
1.函数图象的画法
思考
问题:1.正方形的面积y与边长x的函数解析式为 ,其中x的取值范围是 .
y=x2
x>0
2.怎样获得组成图象的点?
先确定点的坐标.
新知探究
(4)怎样确定满足函数 y= x2( x> 0 )的点的坐标?
取若干自变量x的值,计算出相应的函数y的值,得到若干点的坐标(x,y).
思考
正方形的面积y是边长x的函数,请画出这个函数的图象.
(5)如何将这些点画成函数图象?
将这些点用平滑曲线连接起来
新知小结
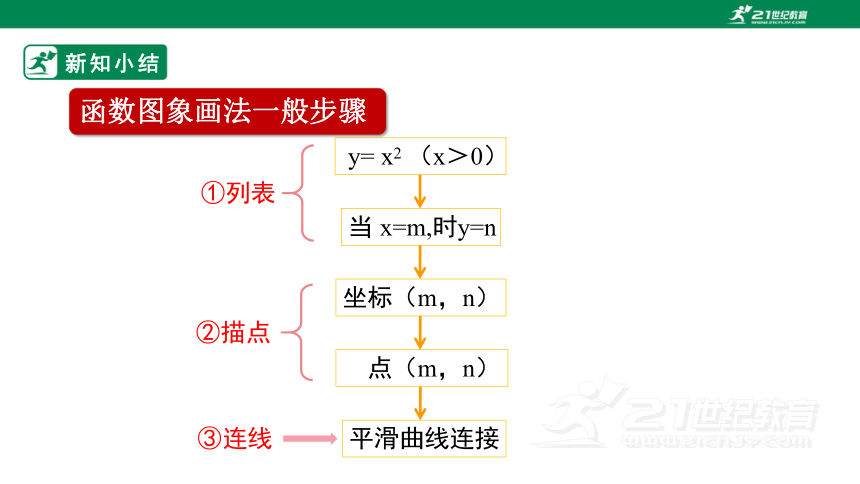
当 x=m,时y=n
坐标(m,n)
点(m,n)
y= x2 (x>0)
函数图象画法一般步骤
平滑曲线连接
①列表
②描点
③连线
新知探究
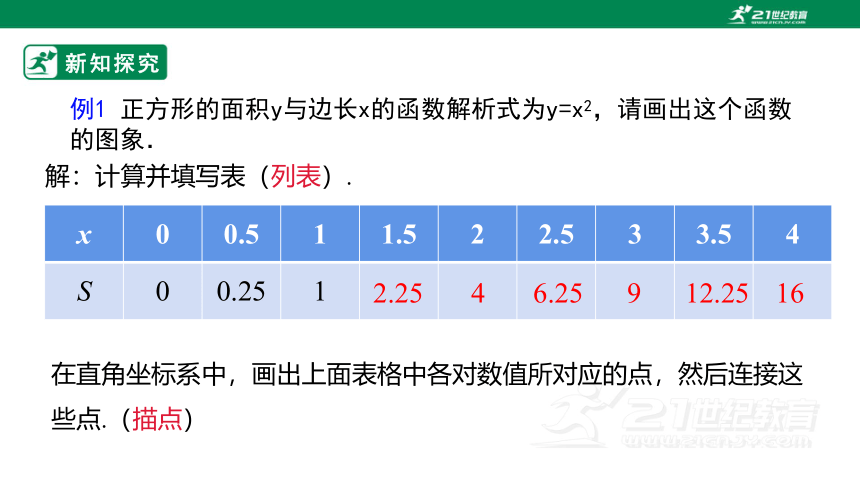
例1 正方形的面积y与边长x的函数解析式为y=x2,请画出这个函数的图象.
解:计算并填写表(列表).
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1
在直角坐标系中,画出上面表格中各对数值所对应的点,然后连接这些点.(描点)
2.25
4
6.25
9
12.25
16
新知探究
O
1
2
3
4
1
4
9
16
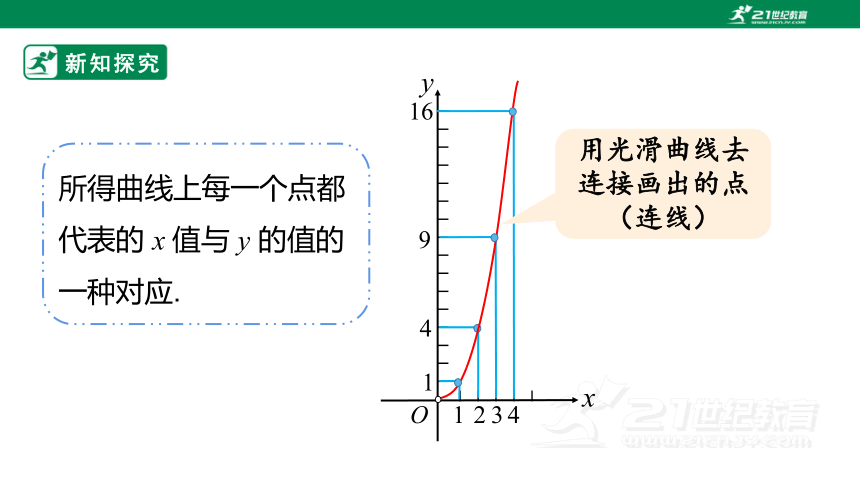
用光滑曲线去连接画出的点
(连线)
所得曲线上每一个点都代表的 x 值与 y 的值的一种对应.
x
y
新知探究
因为该自变量 x 的取值范围是 x>0,所以(0,0)不在曲线上.
用空心圆表示不在曲线的点
用实心圆表示在曲线上的点
新知典例
例2 在式子y = x+0.5中,对于x每一个确定的值,y有唯一的对应值,即y是x的函数,请画出这个函数的图象.
解:自变量x的取值范围为 .
x取全体实数
列表:x取全体实数
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
新知探究
例2 在式子y = x+0.5中,对于x每一个确定的值,y有唯一的对应值,即y是x的函数,请画出这个函数的图象.
②描点
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
③连线
新知练习
练习1:画出函数( x >0 )的图象.
新知练习
x … 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 4 3 2.4 2 1.7 1.5 1.2 1 …
①列表: x取值范围:x>0
练习1:画出函数( x >0 )的图象.
②描点
③连线
图象能与y轴
相交吗?
新知探究
例2 判断下列各点是否在函数y=x+0.5的图象上?
① (-5,-4.5); ②(4,-3.5) .
解: ① ∵x=-5时,y= -5 +0.5= -4.5,
∴ (-5,-4.5)在函数 y=x+0.5的图象上.
② ∵x= 4时,y= 4+0.5= 4.5 ≠- 3.5,
∴(4,-3.5)不在函数y=x+0.5的图象上.
新知练习
练习2.判断下列各点是否在函数的图象上?
①(12,0.5);② (-4.5,-1) .
解: ① ∵x=12时,0.5,
∴ (12,0.5)在函数的图象上.
② ∵x= -4.5时, ≠ -1 ,
∴ (-4.5, -1)不在函数的图象上.
新知典例
y=x+0.5
例3
(1) 观察函数 y=x+0.5的图象,直线从左向右 (上升或下降),x由小变大时,函数y=x+0.5随之 (增大或减小).
上升
增大
新知典例
(2) 观察函数(x>0) 的图象,曲线从左向右 (上升或下降), x由小变大时,函数(x>0) 随之 (增大或减小)
例3
下降
减小
新知练习
练习2
(1)画出函数 y= x2的图象;
(2)判断点A(- 2.5, - 4),B(- 1.6,2.56) 是否在函数 y= x2的图象上.
(3)从函数的图象中观察,当x<0时,y随x增大而增大,还是y 随x 增大而减小?当x>0时呢?
新知练习
练习3
(1)画出函数y= x2的图象;
解:①x取值范围:x取全体实数.
x … -4 -3 -2 -1 0 1 2 3 4 …
y … 16 9 4 1 0 1 4 9 16 …
②列表:
y= x
③描点:
④连线:
新知练习
(2)判断点A(-2.5, -4),B(-1.6,2.56) 是否在
函数y= x2 的图象上.
解:①∵点A(-2.5, -4)在第三象限,
函数y= x2的图象不经过第三象限,
∴点A(-2.5, -4),不在函数y= x 的图象上
②∵x= -1.6时,y= =2.56;
∴ B ( -1.6,2.56)在函数y= x2的图象上.
新知练习
(3)从函数的图象中观察,当x<0时,y随x增大而增大,还是y 随x 增大而减小?当x>0时呢?
解:当x<0时,图象从左向右逐渐下降,y随x增大而减小.
当x > 0时,图象从左向右逐渐上升,y随x增大而增大.
课堂总结
函数的
解析式
函数的
图象
列表
描点
连线
课堂练习
1.摩天轮可以抽象成一个圆,圆上一点离地面的高度 y(m)与旋转时间 x(min)之间的关系如图所示:
课堂练习
(2)变量 y 是 x 的函数吗?为什么?
(1)根据图填表:
x/min …… 0 3 6 8 12 ……
y/m …… ……
y 是 x 的函数,对于每一个确定的 x 的值,都有唯一确定的 y 与之相对应.
5
70
5
54
5
课堂练习
2.已知函数 y = 2x-1.
(1)试判断点A(-1,3)和点B(,)是否在此函数图象上;
(2)已知点(a,a+1)在此函数图象上,求 a 的值.
分析:判断一个点坐标是否在函数图象上,需要将横坐标作为自变量带入函数解析式,看求得的函数值是不是纵坐标.
解:(1)当 x = -1时,y = 2(-1)-1= -33.
所以点 A(-1,3)不在此函数图象上.
当 x = 时,y =2-1= -. 所以点 B(,)在此函数图象上.
课堂练习
解:(2)因为点(a,a+1)在此函数图象上,所以 a+1=2a-1,解得:a=2,即 a 的值为 2.
2.已知函数 y = 2x-1.
(1)试判断点A(-1,3)和点B(,)是否在此函数图象上;
(2)已知点(a,a+1)在此函数图象上,求 a 的值.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
19.1.2函数的图象(2)
人教版八年级下册
知识回顾
①记录下 :
时间t及此时的温度T
②转化为 :
(时间t ,此时的温度T )
③描出对应的 :
点(时间t ,此时的温度T )
函数的图象
数据
坐标
点
教学目标
1.掌握画函数图象的一般步骤,能画出一些简单的函数图象;
2.能解决相关函数图象问题。
新知导入
通过上节课的学习,我们知道了
函数图象就是把自变量与函数的每对对应值分别作为点的 坐标,在平面直角坐标系内由这些点组成的图形.
横、纵
新知探究
正方形的面积y是边长x的函数,请画出这个函数的图象.
1.函数图象的画法
思考
问题:1.正方形的面积y与边长x的函数解析式为 ,其中x的取值范围是 .
y=x2
x>0
2.怎样获得组成图象的点?
先确定点的坐标.
新知探究
(4)怎样确定满足函数 y= x2( x> 0 )的点的坐标?
取若干自变量x的值,计算出相应的函数y的值,得到若干点的坐标(x,y).
思考
正方形的面积y是边长x的函数,请画出这个函数的图象.
(5)如何将这些点画成函数图象?
将这些点用平滑曲线连接起来
新知小结
当 x=m,时y=n
坐标(m,n)
点(m,n)
y= x2 (x>0)
函数图象画法一般步骤
平滑曲线连接
①列表
②描点
③连线
新知探究
例1 正方形的面积y与边长x的函数解析式为y=x2,请画出这个函数的图象.
解:计算并填写表(列表).
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1
在直角坐标系中,画出上面表格中各对数值所对应的点,然后连接这些点.(描点)
2.25
4
6.25
9
12.25
16
新知探究
O
1
2
3
4
1
4
9
16
用光滑曲线去连接画出的点
(连线)
所得曲线上每一个点都代表的 x 值与 y 的值的一种对应.
x
y
新知探究
因为该自变量 x 的取值范围是 x>0,所以(0,0)不在曲线上.
用空心圆表示不在曲线的点
用实心圆表示在曲线上的点
新知典例
例2 在式子y = x+0.5中,对于x每一个确定的值,y有唯一的对应值,即y是x的函数,请画出这个函数的图象.
解:自变量x的取值范围为 .
x取全体实数
列表:x取全体实数
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
新知探究
例2 在式子y = x+0.5中,对于x每一个确定的值,y有唯一的对应值,即y是x的函数,请画出这个函数的图象.
②描点
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
③连线
新知练习
练习1:画出函数( x >0 )的图象.
新知练习
x … 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 4 3 2.4 2 1.7 1.5 1.2 1 …
①列表: x取值范围:x>0
练习1:画出函数( x >0 )的图象.
②描点
③连线
图象能与y轴
相交吗?
新知探究
例2 判断下列各点是否在函数y=x+0.5的图象上?
① (-5,-4.5); ②(4,-3.5) .
解: ① ∵x=-5时,y= -5 +0.5= -4.5,
∴ (-5,-4.5)在函数 y=x+0.5的图象上.
② ∵x= 4时,y= 4+0.5= 4.5 ≠- 3.5,
∴(4,-3.5)不在函数y=x+0.5的图象上.
新知练习
练习2.判断下列各点是否在函数的图象上?
①(12,0.5);② (-4.5,-1) .
解: ① ∵x=12时,0.5,
∴ (12,0.5)在函数的图象上.
② ∵x= -4.5时, ≠ -1 ,
∴ (-4.5, -1)不在函数的图象上.
新知典例
y=x+0.5
例3
(1) 观察函数 y=x+0.5的图象,直线从左向右 (上升或下降),x由小变大时,函数y=x+0.5随之 (增大或减小).
上升
增大
新知典例
(2) 观察函数(x>0) 的图象,曲线从左向右 (上升或下降), x由小变大时,函数(x>0) 随之 (增大或减小)
例3
下降
减小
新知练习
练习2
(1)画出函数 y= x2的图象;
(2)判断点A(- 2.5, - 4),B(- 1.6,2.56) 是否在函数 y= x2的图象上.
(3)从函数的图象中观察,当x<0时,y随x增大而增大,还是y 随x 增大而减小?当x>0时呢?
新知练习
练习3
(1)画出函数y= x2的图象;
解:①x取值范围:x取全体实数.
x … -4 -3 -2 -1 0 1 2 3 4 …
y … 16 9 4 1 0 1 4 9 16 …
②列表:
y= x
③描点:
④连线:
新知练习
(2)判断点A(-2.5, -4),B(-1.6,2.56) 是否在
函数y= x2 的图象上.
解:①∵点A(-2.5, -4)在第三象限,
函数y= x2的图象不经过第三象限,
∴点A(-2.5, -4),不在函数y= x 的图象上
②∵x= -1.6时,y= =2.56;
∴ B ( -1.6,2.56)在函数y= x2的图象上.
新知练习
(3)从函数的图象中观察,当x<0时,y随x增大而增大,还是y 随x 增大而减小?当x>0时呢?
解:当x<0时,图象从左向右逐渐下降,y随x增大而减小.
当x > 0时,图象从左向右逐渐上升,y随x增大而增大.
课堂总结
函数的
解析式
函数的
图象
列表
描点
连线
课堂练习
1.摩天轮可以抽象成一个圆,圆上一点离地面的高度 y(m)与旋转时间 x(min)之间的关系如图所示:
课堂练习
(2)变量 y 是 x 的函数吗?为什么?
(1)根据图填表:
x/min …… 0 3 6 8 12 ……
y/m …… ……
y 是 x 的函数,对于每一个确定的 x 的值,都有唯一确定的 y 与之相对应.
5
70
5
54
5
课堂练习
2.已知函数 y = 2x-1.
(1)试判断点A(-1,3)和点B(,)是否在此函数图象上;
(2)已知点(a,a+1)在此函数图象上,求 a 的值.
分析:判断一个点坐标是否在函数图象上,需要将横坐标作为自变量带入函数解析式,看求得的函数值是不是纵坐标.
解:(1)当 x = -1时,y = 2(-1)-1= -33.
所以点 A(-1,3)不在此函数图象上.
当 x = 时,y =2-1= -. 所以点 B(,)在此函数图象上.
课堂练习
解:(2)因为点(a,a+1)在此函数图象上,所以 a+1=2a-1,解得:a=2,即 a 的值为 2.
2.已知函数 y = 2x-1.
(1)试判断点A(-1,3)和点B(,)是否在此函数图象上;
(2)已知点(a,a+1)在此函数图象上,求 a 的值.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
