2022-2023学年人教版七年级数学下册5.3.1平行线的性质第二课时教学课件课件(共38张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册5.3.1平行线的性质第二课时教学课件课件(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 783.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 12:12:01 | ||
图片预览











文档简介
(共38张PPT)
第五章 相交线平行线
第二课时
5.3.1 平行线的性质
【学习目标】
【学习重点】
【学习难点】
能够综合运用平行线的性质和判定方法解题.
平行线的性质和判定方法的灵活运用.
平行线的性质和判定方法的综合应用.
复习旧知 引入新课
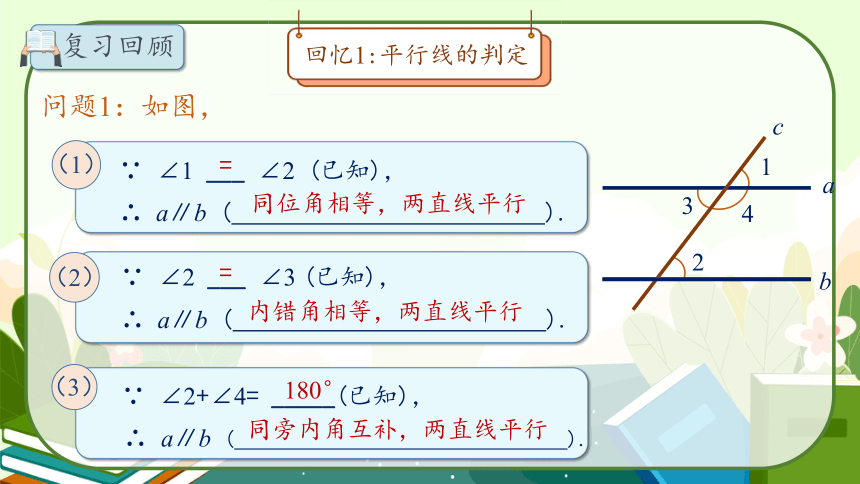
问题1:如图,
∵ ∠2 ___ ∠3 (已知),
∴ a∥b ( ).
∵ ∠2+∠4= _____(已知),
∴ a∥b ( ).
同位角相等,两直线平行
=
内错角相等,两直线平行
180°
同旁内角互补,两直线平行
回忆1:平行线的判定
复习回顾
∵ ∠1 ___ ∠2 (已知),
∴ a∥b ( ).
a
b
c
1
2
3
4
=
(1)
(2)
(3)
(1)
∵ a∥b (已知),
∴ ∠2 ___ ∠3 ( ).
∵ a∥b (已知),
∴ ∠2+∠4= ( ).
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
问题2:如图,
回忆2:平行线的性质
a
b
c
1
2
3
4
复习回顾
(2)
(3)
∵ a∥b (已知),
∴ ∠1 ___ ∠2 ( ).
合作交流 探索新知
平行线的判定与平行线的性质是因果互换的两类不同的定理.
判定是说:满足了什么条件(性质)的两条直线是互相平行的.
性质是说:如果两条直线平行,就应该具有什么性质.
平行线的判定与平行线的性质的比较
(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)同旁内角互补,两直线平行
条件
结论
(3)两直线平行,同旁内角互补
(1)两直线平行,同位角相等
由两个角的相等或互补得到直线的平行
由直线的平行得到两个角的相等或互补
数量
位置
平行线的判定
(2)两直线平行,内错角相等
位置
数量
平行线的性质
条件
结论
条件
结论
同位角相等
内错角相等
同旁内角互补
判定
性质
两直线平行
平行线的性质与平行线的判定什么不同?
结论
条件
应用迁移 巩固提高
如图,已知∠1=∠2,∠B=∠C,说明AB∥CD.
解 :∵ ∠1=∠2(已知),
且 ∠1=∠CGD(对顶角相等),
∴ ∠2=∠CGD(等量代换).
∴ CE∥BF(同位角相等,两直线平行).
∴ ∠BFD=∠C(两直线平行,同位角相等).
又∵ ∠B=∠C(已知),
∴ ∠BFD=∠B(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
A
B
C
D
E
F
H
G
1
2
例1
∴ EF∥CD
(平行于同一直线的两直线相互平行).
A
B
C
D
E
60°
35°
1
2
F
解:过E作EF∥AB,
又∵ AB∥CD,
∴∠1=∠B=60°
(两直线平行,内错角相等).
∴ ∠2=∠D=35°.
∴ ∠BED=∠1+∠2=60°+35°=95°.
已知如图AB∥CD,∠ABE=60°,∠CDE=35°,求∠BED的度数.
例2
已知AB∥CD,要运用平行线的性质,必需构造被第三直
线所截的模型,为此需添加辅助线.
分析
例3
解:∵ CE⊥AB, DF⊥AB,
∴ DF∥EC.
∴ ∠BDF=∠1,∠EDF=∠3.
∵ ED∥AC,
∴ ∠3=∠2.
∴ ∠EDF=∠2.
又 CE平分∠ACB,
∴ ∠1=∠2.
∴ ∠BDF=∠EDF.
如图,在△ABC中,CE⊥AB于点E,DF⊥AB于点F,AC∥ED,CE是∠ACB的平分线,则∠EDF=∠BDF,请说明理由.
A
B
C
D
E
F
1
2
3
显然这两个角没有明显直接的联系,要证明两角相等,
必须分别寻找与∠EDF或∠BDF有等量关系的角.
分析
随堂练习 巩固新知
1.(2019 西湖区校级月考)下列说法中正确的个数有
( )
(1)在同一平面内,不相交的两条直线平行;
(2)垂直于同一直线的两直线平行;
(3)两条直线被第三条直线所截,所得到同位角相等;
(4)两条平行线被第三条直线所截,内错角的角平分线
互相平行.
B
A.1个 B.2个 C.3个 D.4个
2.(2019 普陀区期末)如图,已知∠1=∠2,∠3=65°,那么∠4
的度数是( )
D
3.(2019 霍邱县期末)如图AF平分∠BAC,D在AB上,DE平分
∠BDF且∠1=∠2,则下面四个结论:①DF∥AC;②DE∥AF ;
③∠EDF=∠DFA ; ④∠C+∠DEC=180°,其中成立的有( )
A
A.65° B.95°
C.105° D.115°
A.①②③ B.①②④
C.①③④ D.②③④
1
2
3
4
1
2
B
D
A
C
F
E
证明:∵ ∠BAP+∠APD=180°(已知),
∴ AB∥ ( ).
∴ ∠BAP= ( ).
又∵ ∠1=∠2(已知),
∠3= ﹣∠1,
∠4= ﹣∠2,
∴ AE∥PF( ).
∴ ∠E=∠F( ).
同旁内角互补,两直线平行
CD
∠APC
两直线平行,内错角相等
∠BAP
∠APC
内错角相等两直线平行
两直线平行内错角相等
4.填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
A
B
C
D
E
F
P
1
2
3
4
5.如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交
于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
证明:∵ ∠BHC=∠FHD,∠GFH+∠BHC=180°,
A
B
C
D
G
F
H
1
2
∴ ∠GFH+∠FHD=180°,
∴ FG∥BD,
∴ ∠1=∠ABD,
∵ BD平分∠ABC,
∴ ∠2=∠ABD,
∴ ∠1=∠2.
当堂检测 及时反馈
1.( 2019 鄞州区期中)下列说法正确的有( )
①在同一平面内不相交的两条线段必平行
②过两条直线a,b外一点P,一定可做直线c,使c∥a,
且c∥b
③过直线外一点有且只有一条直线与已知直线平行
④两直线被第三条直线所截得的同旁内角的平分线互
相垂直
B
A.0个 B.1个 C.2个 D.3个
2.(2019 尚志市期末)如图,直线MN分别与直线AB、
CD相交于点E、F,∠MEB与∠CFE互补,∠BEF的
平分线与∠DFE的平分线交于点P,与直线CD交于点
G,GH∥PF交MN于点H,则下列说法中错误的是
( )
D
A.AB∥CD B.∠FGE=∠FEG
C.EG⊥GH D.∠EFC=∠EGD
A
E
B
M
D
G
P
H
N
C
F
3.将一副直角三角尺ABC和CDE按如图方
式放置,其中直角顶点C 重合,∠D=45°,
∠A=30°.若DE∥BC,则∠1的大小为 .
105°
1
A
B
C
D
E
4.已知直线m∥n,将一块含30°角的直角三
角板ABC,按如图方式放置(∠ABC=30°),
其中A,B两点分别落在直线m,n上,若
∠1=18°,则∠2= .
48°
1
2
A
B
C
5.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
解:(1)∵ AC∥DE,
(2)∵ ∠1=68°,DF∥BC,
A
B
C
D
E
F
1
∴ ∠C=∠1,
∵ ∠AFD=∠1,
∴ ∠C=∠AFD,
∴ DF∥BC.
∴ ∠EDF=∠1=68°,
∵ DF平分∠ADE,
∴ ∠ADF=∠EDF=68°,
∵ DF∥BC,
∴ ∠B=∠ADF=68°.
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,AF
平分∠BAD,∠BAD=2∠F.
(1)AD与BC平行吗?请说明理由.
(2)AB与EF的位置关系如何?为什么?
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;
②∠E+∠F=90°.
解:(1)AD∥BC,理由如下:
∵ ∠ADE+∠BCF=180°,∠ADE+∠ADC=180°,
∴ ∠BCF=∠ADC,
∴ AD∥BC.
A
D
E
C
F
B
O
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,
AF平分∠BAD,∠BAD=2∠F.
(2)AB与EF的位置关系如何?为什么?
(2)AB∥EF,理由如下:
∵ AF平分∠BAD,∠BAD=2∠F,
∴ ∠BAF=∠BAD=∠F,
∴ AB∥EF.
A
D
E
C
F
B
O
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,
AF平分∠BAD,∠BAD=2∠F.
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②
∠E+∠F=90°.
(3)①∠ABC=2∠E,理由如下:
A
D
E
C
F
B
O
∵ AB∥EF,
∴ ∠ABE=∠E.
∵ BE平分∠ABC,
∴ ∠ABC=2∠ABE=2∠E.
∵ AD∥BC,
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,
AF平分∠BAD,∠BAD=2∠F.
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②
∠E+∠F=90°.
(3)②∠E+∠F=90°,理由如下:
∴ ∠BAD+∠ABC=180°.
∵ ∠BAD=2∠F,∠ABC=2∠E,
∴ 2∠E+2∠F=180°,
∴ ∠E+∠F=90°.
A
D
E
C
F
B
O
拓展延升 能力提升
1.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点
A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM
于点C,D.
(1)求∠CBD的度数;
A
B
C
D
M
N
P
解:(1)∵ AM∥BN,
∴ ∠ABN=180°-∠A=120°,
又∵ BC,BD分别平分∠ABP和∠PBN,
∴ ∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN )=∠ABN=60°.
1.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点
A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM
于点C,D.
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不
变,请求出这个比值;若变化,请找出变化规律;
(2)不变.理由如下:
∵ AM∥BN,
∴ ∠APB=∠PBN,∠ADB=∠DBN,
又∵ BD平分∠PBN,
∴ ∠ADB=∠DBN=∠PBN=∠APB,
A
B
C
D
M
N
P
即 ∠APB:∠ADB=2:1.
(3)∵ AM∥BN,
1.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点
A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM
于点C,D.
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
A
B
C
D
M
N
P
∴ ∠ACB=∠CBN,
又∵ ∠ACB=∠ABD,
∴ ∠CBN=∠ABD,∴ ∠CBN=∠ABD,
∴ ∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
∴ ∠ABC=∠CBP=∠DBP=∠DBN,
∴ ∠ABC=∠ABN=30°.
2.已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,
∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线
相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,
∠AKC与∠APC有何数量关系?并说明理由.
A
C
D
B
P
图1
A
C
D
B
P
K
图2
A
C
D
B
P
图3
K
∴ ∠APC=∠APE+∠CPE
=∠BAP+∠DCP=60°+20°=80°.
解:(1)如图1,过P作PE∥AB,
A
C
D
B
P
图1
E
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°
∠DCP=20°时,求∠APC.
∵ AB∥CD,
∴ PE∥AB∥CD,
∴ ∠APE=∠BAP,CPE=∠DCP,
C
图2
解: (2)∠AKC=∠APC.
A
D
B
P
K
F
E
理由:过K作KE∥AB,过P作PF∥AB,
∵ AB∥CD,∴ KE∥AB∥CD,
∴ ∠AKE=∠BAK,∠CKE=∠DCK,
∴ ∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
同理可得,∠APC=∠BAP+∠DCP,
∵ ∠BAP与∠DCP的角平分线相交于点K,
∴ ∠BAK+∠DCK=∠BAP+∠DCP=∠APC,
∴ ∠AKC=∠APC.
(3) ∠AKC=∠APC.
A
C
D
B
P
K
E
理由:过K作KE∥AB,过P作PF∥AB,
∵ AB∥CD,
∴ KE∥AB∥CD,
∴ ∠BAK=∠AKE,∠DCK=∠CKE,
∴ ∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,
同理可得,∠APC=∠BAP-∠DCP,
∵ ∠BAP与∠DCP的角平分线相交于点K,
∴ ∠BAK-∠DCK=∠BAP-∠DCP=∠APC,
∴ ∠AKC=∠APC.
F
识记 理解 掌握 应用 综合 评价
平行线的判定与性质的综合应用 练1 例1 练2 练3 测1 例2 练4 测2 测3 测4 例3 练5 测5 测6 拓1 拓2
知识点
能力层次
练习知识双向细目表
总结反思 知识内化
小 结
因果转换
判 定
同位角相等
内错角相等
同旁内角互补
两直线平行
性 质
数量
位置
数量
位置
第五章 相交线平行线
第二课时
5.3.1 平行线的性质
【学习目标】
【学习重点】
【学习难点】
能够综合运用平行线的性质和判定方法解题.
平行线的性质和判定方法的灵活运用.
平行线的性质和判定方法的综合应用.
复习旧知 引入新课
问题1:如图,
∵ ∠2 ___ ∠3 (已知),
∴ a∥b ( ).
∵ ∠2+∠4= _____(已知),
∴ a∥b ( ).
同位角相等,两直线平行
=
内错角相等,两直线平行
180°
同旁内角互补,两直线平行
回忆1:平行线的判定
复习回顾
∵ ∠1 ___ ∠2 (已知),
∴ a∥b ( ).
a
b
c
1
2
3
4
=
(1)
(2)
(3)
(1)
∵ a∥b (已知),
∴ ∠2 ___ ∠3 ( ).
∵ a∥b (已知),
∴ ∠2+∠4= ( ).
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
问题2:如图,
回忆2:平行线的性质
a
b
c
1
2
3
4
复习回顾
(2)
(3)
∵ a∥b (已知),
∴ ∠1 ___ ∠2 ( ).
合作交流 探索新知
平行线的判定与平行线的性质是因果互换的两类不同的定理.
判定是说:满足了什么条件(性质)的两条直线是互相平行的.
性质是说:如果两条直线平行,就应该具有什么性质.
平行线的判定与平行线的性质的比较
(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)同旁内角互补,两直线平行
条件
结论
(3)两直线平行,同旁内角互补
(1)两直线平行,同位角相等
由两个角的相等或互补得到直线的平行
由直线的平行得到两个角的相等或互补
数量
位置
平行线的判定
(2)两直线平行,内错角相等
位置
数量
平行线的性质
条件
结论
条件
结论
同位角相等
内错角相等
同旁内角互补
判定
性质
两直线平行
平行线的性质与平行线的判定什么不同?
结论
条件
应用迁移 巩固提高
如图,已知∠1=∠2,∠B=∠C,说明AB∥CD.
解 :∵ ∠1=∠2(已知),
且 ∠1=∠CGD(对顶角相等),
∴ ∠2=∠CGD(等量代换).
∴ CE∥BF(同位角相等,两直线平行).
∴ ∠BFD=∠C(两直线平行,同位角相等).
又∵ ∠B=∠C(已知),
∴ ∠BFD=∠B(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
A
B
C
D
E
F
H
G
1
2
例1
∴ EF∥CD
(平行于同一直线的两直线相互平行).
A
B
C
D
E
60°
35°
1
2
F
解:过E作EF∥AB,
又∵ AB∥CD,
∴∠1=∠B=60°
(两直线平行,内错角相等).
∴ ∠2=∠D=35°.
∴ ∠BED=∠1+∠2=60°+35°=95°.
已知如图AB∥CD,∠ABE=60°,∠CDE=35°,求∠BED的度数.
例2
已知AB∥CD,要运用平行线的性质,必需构造被第三直
线所截的模型,为此需添加辅助线.
分析
例3
解:∵ CE⊥AB, DF⊥AB,
∴ DF∥EC.
∴ ∠BDF=∠1,∠EDF=∠3.
∵ ED∥AC,
∴ ∠3=∠2.
∴ ∠EDF=∠2.
又 CE平分∠ACB,
∴ ∠1=∠2.
∴ ∠BDF=∠EDF.
如图,在△ABC中,CE⊥AB于点E,DF⊥AB于点F,AC∥ED,CE是∠ACB的平分线,则∠EDF=∠BDF,请说明理由.
A
B
C
D
E
F
1
2
3
显然这两个角没有明显直接的联系,要证明两角相等,
必须分别寻找与∠EDF或∠BDF有等量关系的角.
分析
随堂练习 巩固新知
1.(2019 西湖区校级月考)下列说法中正确的个数有
( )
(1)在同一平面内,不相交的两条直线平行;
(2)垂直于同一直线的两直线平行;
(3)两条直线被第三条直线所截,所得到同位角相等;
(4)两条平行线被第三条直线所截,内错角的角平分线
互相平行.
B
A.1个 B.2个 C.3个 D.4个
2.(2019 普陀区期末)如图,已知∠1=∠2,∠3=65°,那么∠4
的度数是( )
D
3.(2019 霍邱县期末)如图AF平分∠BAC,D在AB上,DE平分
∠BDF且∠1=∠2,则下面四个结论:①DF∥AC;②DE∥AF ;
③∠EDF=∠DFA ; ④∠C+∠DEC=180°,其中成立的有( )
A
A.65° B.95°
C.105° D.115°
A.①②③ B.①②④
C.①③④ D.②③④
1
2
3
4
1
2
B
D
A
C
F
E
证明:∵ ∠BAP+∠APD=180°(已知),
∴ AB∥ ( ).
∴ ∠BAP= ( ).
又∵ ∠1=∠2(已知),
∠3= ﹣∠1,
∠4= ﹣∠2,
∴ AE∥PF( ).
∴ ∠E=∠F( ).
同旁内角互补,两直线平行
CD
∠APC
两直线平行,内错角相等
∠BAP
∠APC
内错角相等两直线平行
两直线平行内错角相等
4.填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
A
B
C
D
E
F
P
1
2
3
4
5.如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交
于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
证明:∵ ∠BHC=∠FHD,∠GFH+∠BHC=180°,
A
B
C
D
G
F
H
1
2
∴ ∠GFH+∠FHD=180°,
∴ FG∥BD,
∴ ∠1=∠ABD,
∵ BD平分∠ABC,
∴ ∠2=∠ABD,
∴ ∠1=∠2.
当堂检测 及时反馈
1.( 2019 鄞州区期中)下列说法正确的有( )
①在同一平面内不相交的两条线段必平行
②过两条直线a,b外一点P,一定可做直线c,使c∥a,
且c∥b
③过直线外一点有且只有一条直线与已知直线平行
④两直线被第三条直线所截得的同旁内角的平分线互
相垂直
B
A.0个 B.1个 C.2个 D.3个
2.(2019 尚志市期末)如图,直线MN分别与直线AB、
CD相交于点E、F,∠MEB与∠CFE互补,∠BEF的
平分线与∠DFE的平分线交于点P,与直线CD交于点
G,GH∥PF交MN于点H,则下列说法中错误的是
( )
D
A.AB∥CD B.∠FGE=∠FEG
C.EG⊥GH D.∠EFC=∠EGD
A
E
B
M
D
G
P
H
N
C
F
3.将一副直角三角尺ABC和CDE按如图方
式放置,其中直角顶点C 重合,∠D=45°,
∠A=30°.若DE∥BC,则∠1的大小为 .
105°
1
A
B
C
D
E
4.已知直线m∥n,将一块含30°角的直角三
角板ABC,按如图方式放置(∠ABC=30°),
其中A,B两点分别落在直线m,n上,若
∠1=18°,则∠2= .
48°
1
2
A
B
C
5.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
解:(1)∵ AC∥DE,
(2)∵ ∠1=68°,DF∥BC,
A
B
C
D
E
F
1
∴ ∠C=∠1,
∵ ∠AFD=∠1,
∴ ∠C=∠AFD,
∴ DF∥BC.
∴ ∠EDF=∠1=68°,
∵ DF平分∠ADE,
∴ ∠ADF=∠EDF=68°,
∵ DF∥BC,
∴ ∠B=∠ADF=68°.
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,AF
平分∠BAD,∠BAD=2∠F.
(1)AD与BC平行吗?请说明理由.
(2)AB与EF的位置关系如何?为什么?
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;
②∠E+∠F=90°.
解:(1)AD∥BC,理由如下:
∵ ∠ADE+∠BCF=180°,∠ADE+∠ADC=180°,
∴ ∠BCF=∠ADC,
∴ AD∥BC.
A
D
E
C
F
B
O
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,
AF平分∠BAD,∠BAD=2∠F.
(2)AB与EF的位置关系如何?为什么?
(2)AB∥EF,理由如下:
∵ AF平分∠BAD,∠BAD=2∠F,
∴ ∠BAF=∠BAD=∠F,
∴ AB∥EF.
A
D
E
C
F
B
O
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,
AF平分∠BAD,∠BAD=2∠F.
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②
∠E+∠F=90°.
(3)①∠ABC=2∠E,理由如下:
A
D
E
C
F
B
O
∵ AB∥EF,
∴ ∠ABE=∠E.
∵ BE平分∠ABC,
∴ ∠ABC=2∠ABE=2∠E.
∵ AD∥BC,
6.(2019 西湖区校级月考)如图,∠ADE+∠BCF=180°,
AF平分∠BAD,∠BAD=2∠F.
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②
∠E+∠F=90°.
(3)②∠E+∠F=90°,理由如下:
∴ ∠BAD+∠ABC=180°.
∵ ∠BAD=2∠F,∠ABC=2∠E,
∴ 2∠E+2∠F=180°,
∴ ∠E+∠F=90°.
A
D
E
C
F
B
O
拓展延升 能力提升
1.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点
A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM
于点C,D.
(1)求∠CBD的度数;
A
B
C
D
M
N
P
解:(1)∵ AM∥BN,
∴ ∠ABN=180°-∠A=120°,
又∵ BC,BD分别平分∠ABP和∠PBN,
∴ ∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN )=∠ABN=60°.
1.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点
A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM
于点C,D.
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不
变,请求出这个比值;若变化,请找出变化规律;
(2)不变.理由如下:
∵ AM∥BN,
∴ ∠APB=∠PBN,∠ADB=∠DBN,
又∵ BD平分∠PBN,
∴ ∠ADB=∠DBN=∠PBN=∠APB,
A
B
C
D
M
N
P
即 ∠APB:∠ADB=2:1.
(3)∵ AM∥BN,
1.如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点
A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM
于点C,D.
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
A
B
C
D
M
N
P
∴ ∠ACB=∠CBN,
又∵ ∠ACB=∠ABD,
∴ ∠CBN=∠ABD,∴ ∠CBN=∠ABD,
∴ ∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
∴ ∠ABC=∠CBP=∠DBP=∠DBN,
∴ ∠ABC=∠ABN=30°.
2.已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,
∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线
相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,
∠AKC与∠APC有何数量关系?并说明理由.
A
C
D
B
P
图1
A
C
D
B
P
K
图2
A
C
D
B
P
图3
K
∴ ∠APC=∠APE+∠CPE
=∠BAP+∠DCP=60°+20°=80°.
解:(1)如图1,过P作PE∥AB,
A
C
D
B
P
图1
E
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°
∠DCP=20°时,求∠APC.
∵ AB∥CD,
∴ PE∥AB∥CD,
∴ ∠APE=∠BAP,CPE=∠DCP,
C
图2
解: (2)∠AKC=∠APC.
A
D
B
P
K
F
E
理由:过K作KE∥AB,过P作PF∥AB,
∵ AB∥CD,∴ KE∥AB∥CD,
∴ ∠AKE=∠BAK,∠CKE=∠DCK,
∴ ∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
同理可得,∠APC=∠BAP+∠DCP,
∵ ∠BAP与∠DCP的角平分线相交于点K,
∴ ∠BAK+∠DCK=∠BAP+∠DCP=∠APC,
∴ ∠AKC=∠APC.
(3) ∠AKC=∠APC.
A
C
D
B
P
K
E
理由:过K作KE∥AB,过P作PF∥AB,
∵ AB∥CD,
∴ KE∥AB∥CD,
∴ ∠BAK=∠AKE,∠DCK=∠CKE,
∴ ∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,
同理可得,∠APC=∠BAP-∠DCP,
∵ ∠BAP与∠DCP的角平分线相交于点K,
∴ ∠BAK-∠DCK=∠BAP-∠DCP=∠APC,
∴ ∠AKC=∠APC.
F
识记 理解 掌握 应用 综合 评价
平行线的判定与性质的综合应用 练1 例1 练2 练3 测1 例2 练4 测2 测3 测4 例3 练5 测5 测6 拓1 拓2
知识点
能力层次
练习知识双向细目表
总结反思 知识内化
小 结
因果转换
判 定
同位角相等
内错角相等
同旁内角互补
两直线平行
性 质
数量
位置
数量
位置
