冀教版数学七年级下册8.4.2 单项式与多项式相乘 导学课件(共38张PPT)
文档属性
| 名称 | 冀教版数学七年级下册8.4.2 单项式与多项式相乘 导学课件(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 13:00:02 | ||
图片预览










文档简介
(共38张PPT)
8.4 整式的乘法
第8章 整式的乘法
第2课时 单项式与多项式
相乘
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
单项式与多项式相乘的法则
单项式与多项式相乘法则的应用
课时导入
旧知回顾
单项式与单项式相乘,只要把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里出现的字母,则连同它的指数一起作为积的一个因式。
课时导入
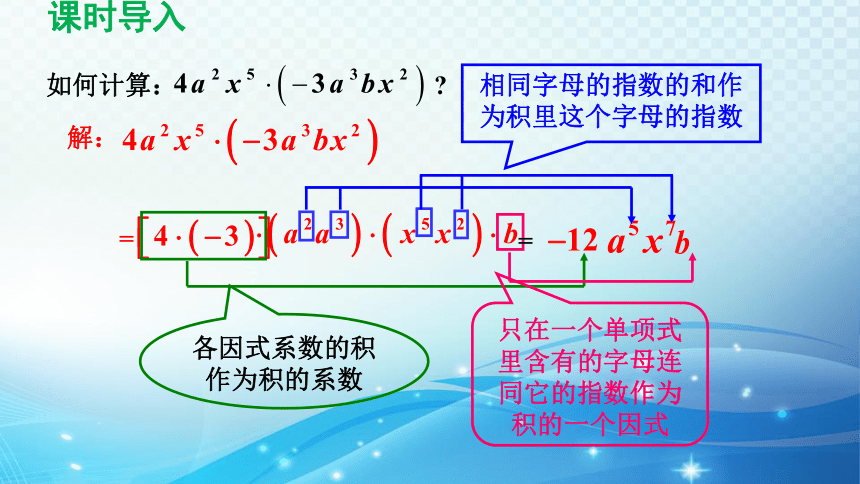
如何计算:
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
课时导入
怎样计算m(a+b)呢?
m是一个单项式,a+b是一个多项式,这是一个单
项式与多项式相乘的问题.
由于字母a,b都代表数,所以可以用分配律进行
计算,即
m(a+b)=ma+mb.
知识点
单项式与多项式相乘的法则
感悟新知
1
如下图,学校有一块长为a米,宽为b米的矩形
操场,现在要割出一块边长分别为2c、b米的矩形
场地作篮球场,试用不同的方法表示余下的场地的
面积。从不同的表示方法中,你能得到什么结论?
b
a
2c
b
(1) s=b(a–2c) (2) s=ba–b·2c
由(1) 、(2) 可知b (a–2c) =ba–b·2c
归 纳
感悟新知
单项式与多项式相乘,用单项式去乘多项式的每
一项,再把积相加.
感悟新知
(1)单项式与多项式相乘,实质上是利用乘法分配律将
其转化为单项式乘以单项式的问题.
(2)单项式与多项式相乘,结果是一个多项式,其项数
与因式中多项式的项数相同.
(3)计算过程要注意符号,单项式乘多项式的每一项时,
要包括它前面的符号,同时还要注意单项式的符号.
(4)对于混合运算,应注意运算顺序;最后有同类项时,
必须合并同类项从而得到最简结果.
感悟新知
例 1
解:
计算:
(1) ab(a2+b2) ;(2) -x(2x-3) .
(1) ab(a2+b2)
=ab·a2+ab·b2
=a3b+ab3.
(2) -x(2x-3)
=(-x)×(2x)+ (-x)×(-3)
=-2x2+3x.
归 纳
感悟新知
单项式与多项式相乘时,依据法则将其转化为
单项式与单项式相乘,相乘每两项的积用“+”号
相连,然后按单项式与单项式相乘的法则逐个计算,
特别要注意符号.
感悟新知
1.
解:
计算:
(1) 8b2(2a2-ab-b2); (2) ab2 (3a -6b).
(1)8b2(2a2-ab-b2)=8b2·2a2-8b2·ab-8b2·b2
=16a2b2-8ab3-8b4.
(2) ab2(3a-6b)= ab2·3a- ab2·6b
=2a2b2-4ab3.
感悟新知
2.
计算:
(1)3x(4x2y-2xy2);
(2)3a(2a2-a+2);
(3)(-2ab)2·(3a+2b-1);
(4) ·(-4x).
感悟新知
解:
(1)3x(4x2y-2xy2)=3x·4x2y-3x·2xy2=12x3y-6x2y2.
(2)3a(2a2-a+2)=3a·2a2-3a·a+3a·2=6a3-3a2+6a.
(3)(-2ab)2·(3a+2b-1)=4a2b2·(3a+2b-1)=4a2b2·3a+4a2b2·2b-4a2b2=12a3b2+8a2b3-4a2b2.
感悟新知
(4) ·(-4x)
= xy·(-4x)- y·(-4x)-y2·(-4x)
=-3x2y+2xy+4xy2.
感悟新知
3.
计算:
(1)a(a-b)+3b(a+4b);
(2)3a(a2+3a-2)-3(a3+2a2-a+1) ;
(3)2x(-xy)2-x2(x2y2-y2).
感悟新知
解:
(1)a(a-b)+3b(a+4b)=a2-ab+3ab+12b2=a2+2ab+12b2.
(2)3a(a2+3a-2)-3(a3+2a2-a+1)=3a3+9a2-6a-3a3-6a2+3a-3=3a2-3a-3.
(3)2x(-xy)2-x2(x2y2-y2)=2x·x2y2-x2(x2y2-y2)=2x3y2-x4y2+x2y2.
感悟新知
4.
计算: 2ab(a2b+ab-ab2)-ab2(a2-2ab+2a)
2ab(a2b+ab-ab2)-ab2(a2-2ab+2a)=2ab·a2b+2ab·ab-2ab·ab2-ab2·a2+ab2·2ab-ab2·2a=2a3b2+2a2b2-2a2b3-a3b2+2a2b3-2a2b2=a3b2.
解:
感悟新知
7.
下列运算错误的是( )
A.-m2·m3=-m5
B.-x2+2x2=x2
C.(-a3b)2=a6b2
D.-2x(x-y)=-2x2-2xy
D
感悟新知
8.
如果一个长方形的周长为10,其中长为a,那么该长方形的面积为( )
A.10a B.5a-a2
C.5a D.10a-a2
B
感悟新知
9.
下列计算错误的是( )
A.-3x(2-x)=-6x+3x2
B.(2m2n-3mn2)(-mn)=-2m3n2+3m2n3
C.xy(x2y-xy2-1)=x3y2-x2y3
D.
C
感悟新知
知识点
单项式与多项式相乘法则的应用
2
例2
先化简,再求值: a2(a+1)-a (a2-1).
其中,a=5.
a2(a+1)-a (a2-1)
=a3+a2-a3+a
=a2+a
当a=5时,原式=52+5=30
解:
归 纳
感悟新知
化简求值得题目,先化简再求值,化简的过程
包括整式的乘法与加减法运算,求值的过程就是直
接代入求值.
感悟新知
1.
解:
先化简,再求值: 2x(x-3y-1)+y(6x-y+2).
其中,x=-3,y=2.
2x(x-3y-1)+y(6x-y+2)=2x·x-2x·3y-2x+6xy-y·y+2y=2x2-2x-y2+2y.
当x=-3,y=2时,原式=2×(-3)2-2×(-3)-22+2×2=18+6-4+4=24.
感悟新知
2.
先化简,再求值:
ab(ab-2a+2)-2b(a2b-2ab+2a).
其中,a=-1,b=-2.
感悟新知
ab(ab-2a+2)-2b(a2b-2ab+2a)=ab·ab-ab·2a+ab·2-2b·a2b+2b·2ab-2b·2a=a2b2-2a2b+2ab-2a2b2+4ab2-4ab=-a2b2-2a2b+4ab2-2ab.
当a=-1,b=-2时,原式=-(-1)2×(-2)2-2×(-1)2×(-2)+4×(-1)×(-2)2-2×(-1) ×(-2)=-4+4-16-4=-20.
解:
感悟新知
3.
解方程: x(x-3)+2x(x+2)=3x2-5.
去括号,得x2-3x+2x2+4x=3x2-5.
移项,得x2-3x+2x2+4x-3x2=-5.
合并同类项,得x=-5.
解:
感悟新知
4.
计算下列物体的体积和表面积:
感悟新知
解:
圆柱:体积V=πr2·(3r+3)=3πr3+3πr2;
表面积S=2πr2+2πr(3r+3)=2πr2+6πr2+6πr=8πr2+6πr.
长方体:体积V=(4a-1)·a·2a=8a3-2a2;
表面积S=2[2a·(4a-1)+2a·a+a·(4a-1)]=2(8a2-2a+2a2+4a2-a)=2(14a2-3a)=28a2-6a.
感悟新知
5.
今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy (4y-2x-1)=-12xy2+6x2y+□,□的地方被钢笔水弄污了,你认为□内应填写( )
A.3xy B.-3xy
C.-1 D.1
A
感悟新知
6.
要使x(x+a)+3x-2b=x2+5x+4成立,则a,b的值分别为( )
A.a=-2,b=-2 B.a=2,b=2
C.a=2,b=-2 D.a=-2,b=2
若计算(x2+ax+5)·(-2x)-6x2的结果中不含有x2项,则a的值为( )
A.-3 B.-
C.0 D.3
C
A
7.
感悟新知
8.
如图,通过计算大长方形的面积可得到的恒等式为________________________.
2a(a+b)=2a2+2ab
感悟新知
9.
化简:
(1)(-2ab)(3a2-2ab-4b2);
(2)3x(2x-3y)-(2x-5y)·4x;
(3)5a(a-b+c)-2b(a+b-c)-4c(-a-b-c).
(1)原式=-6a3b+4a2b2+8ab3.
(2)原式=6x2-9xy-8x2+20xy=-2x2+11xy.
(3)原式=5a2-5ab+5ac-2ab-2b2+2bc+4ac+4bc+4c2=5a2-2b2+4c2-7ab+9ac+6bc.
解:
感悟新知
10.
解:
先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),
其中a=-2.
原式=6a3-12a2+9a-6a3-8a2=-20a2+9a,
当a=-2时,原式=-20×4-9×2=-98.
感悟新知
11.
解:
解方程:2x(x-1)=12+x(2x-5).
去括号,得2x2-2x=12+2x2-5x,
移项、合并同类项,得3x=12,
系数化为1,得x=4.
本节小结
单项式与多项
式相乘
1. 单项式与多项式相乘的依据是:乘法对加法的分配
律.
2. 单项式与多项式相乘,其积仍是多项式,项数与原
多项式的项数 相同,注意不要漏乘项.
3. 积的每一项的符号由原多项式各项符号和单项式的
符号来决定,注意去括号法则.
本节小结
单项式与多项
式相乘
下列运算中,正确的是( )
A.-2x(3x2y-2xy)=-6x3y-4x2y
B.2xy2(-x2+2y2+1)=-4x3y4
C.(3ab2-2ab)·abc=3a2b3-2a2b2
D.(ab)2(2ab2-c)=2a3b4-a2b2c
D
易错点:对单项式与多项式相乘的法则理解不透而出错
本节小结
点拨:
单项式与单项
式相乘
单项式与多项式相乘时,A中多项式的每一项都包括其前面的符号,单项式如果含有负号,运算时容易漏掉单项式的负号,或多项式中每一项的符号而产生错解.B中单项式要与多项式中的每一项相乘,不能漏项.C中单项式与单项式相乘时,对于只在一个单项式里含有的字母,容易漏掉.
请完成教材课后习题
作业提升
8.4 整式的乘法
第8章 整式的乘法
第2课时 单项式与多项式
相乘
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
单项式与多项式相乘的法则
单项式与多项式相乘法则的应用
课时导入
旧知回顾
单项式与单项式相乘,只要把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里出现的字母,则连同它的指数一起作为积的一个因式。
课时导入
如何计算:
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
课时导入
怎样计算m(a+b)呢?
m是一个单项式,a+b是一个多项式,这是一个单
项式与多项式相乘的问题.
由于字母a,b都代表数,所以可以用分配律进行
计算,即
m(a+b)=ma+mb.
知识点
单项式与多项式相乘的法则
感悟新知
1
如下图,学校有一块长为a米,宽为b米的矩形
操场,现在要割出一块边长分别为2c、b米的矩形
场地作篮球场,试用不同的方法表示余下的场地的
面积。从不同的表示方法中,你能得到什么结论?
b
a
2c
b
(1) s=b(a–2c) (2) s=ba–b·2c
由(1) 、(2) 可知b (a–2c) =ba–b·2c
归 纳
感悟新知
单项式与多项式相乘,用单项式去乘多项式的每
一项,再把积相加.
感悟新知
(1)单项式与多项式相乘,实质上是利用乘法分配律将
其转化为单项式乘以单项式的问题.
(2)单项式与多项式相乘,结果是一个多项式,其项数
与因式中多项式的项数相同.
(3)计算过程要注意符号,单项式乘多项式的每一项时,
要包括它前面的符号,同时还要注意单项式的符号.
(4)对于混合运算,应注意运算顺序;最后有同类项时,
必须合并同类项从而得到最简结果.
感悟新知
例 1
解:
计算:
(1) ab(a2+b2) ;(2) -x(2x-3) .
(1) ab(a2+b2)
=ab·a2+ab·b2
=a3b+ab3.
(2) -x(2x-3)
=(-x)×(2x)+ (-x)×(-3)
=-2x2+3x.
归 纳
感悟新知
单项式与多项式相乘时,依据法则将其转化为
单项式与单项式相乘,相乘每两项的积用“+”号
相连,然后按单项式与单项式相乘的法则逐个计算,
特别要注意符号.
感悟新知
1.
解:
计算:
(1) 8b2(2a2-ab-b2); (2) ab2 (3a -6b).
(1)8b2(2a2-ab-b2)=8b2·2a2-8b2·ab-8b2·b2
=16a2b2-8ab3-8b4.
(2) ab2(3a-6b)= ab2·3a- ab2·6b
=2a2b2-4ab3.
感悟新知
2.
计算:
(1)3x(4x2y-2xy2);
(2)3a(2a2-a+2);
(3)(-2ab)2·(3a+2b-1);
(4) ·(-4x).
感悟新知
解:
(1)3x(4x2y-2xy2)=3x·4x2y-3x·2xy2=12x3y-6x2y2.
(2)3a(2a2-a+2)=3a·2a2-3a·a+3a·2=6a3-3a2+6a.
(3)(-2ab)2·(3a+2b-1)=4a2b2·(3a+2b-1)=4a2b2·3a+4a2b2·2b-4a2b2=12a3b2+8a2b3-4a2b2.
感悟新知
(4) ·(-4x)
= xy·(-4x)- y·(-4x)-y2·(-4x)
=-3x2y+2xy+4xy2.
感悟新知
3.
计算:
(1)a(a-b)+3b(a+4b);
(2)3a(a2+3a-2)-3(a3+2a2-a+1) ;
(3)2x(-xy)2-x2(x2y2-y2).
感悟新知
解:
(1)a(a-b)+3b(a+4b)=a2-ab+3ab+12b2=a2+2ab+12b2.
(2)3a(a2+3a-2)-3(a3+2a2-a+1)=3a3+9a2-6a-3a3-6a2+3a-3=3a2-3a-3.
(3)2x(-xy)2-x2(x2y2-y2)=2x·x2y2-x2(x2y2-y2)=2x3y2-x4y2+x2y2.
感悟新知
4.
计算: 2ab(a2b+ab-ab2)-ab2(a2-2ab+2a)
2ab(a2b+ab-ab2)-ab2(a2-2ab+2a)=2ab·a2b+2ab·ab-2ab·ab2-ab2·a2+ab2·2ab-ab2·2a=2a3b2+2a2b2-2a2b3-a3b2+2a2b3-2a2b2=a3b2.
解:
感悟新知
7.
下列运算错误的是( )
A.-m2·m3=-m5
B.-x2+2x2=x2
C.(-a3b)2=a6b2
D.-2x(x-y)=-2x2-2xy
D
感悟新知
8.
如果一个长方形的周长为10,其中长为a,那么该长方形的面积为( )
A.10a B.5a-a2
C.5a D.10a-a2
B
感悟新知
9.
下列计算错误的是( )
A.-3x(2-x)=-6x+3x2
B.(2m2n-3mn2)(-mn)=-2m3n2+3m2n3
C.xy(x2y-xy2-1)=x3y2-x2y3
D.
C
感悟新知
知识点
单项式与多项式相乘法则的应用
2
例2
先化简,再求值: a2(a+1)-a (a2-1).
其中,a=5.
a2(a+1)-a (a2-1)
=a3+a2-a3+a
=a2+a
当a=5时,原式=52+5=30
解:
归 纳
感悟新知
化简求值得题目,先化简再求值,化简的过程
包括整式的乘法与加减法运算,求值的过程就是直
接代入求值.
感悟新知
1.
解:
先化简,再求值: 2x(x-3y-1)+y(6x-y+2).
其中,x=-3,y=2.
2x(x-3y-1)+y(6x-y+2)=2x·x-2x·3y-2x+6xy-y·y+2y=2x2-2x-y2+2y.
当x=-3,y=2时,原式=2×(-3)2-2×(-3)-22+2×2=18+6-4+4=24.
感悟新知
2.
先化简,再求值:
ab(ab-2a+2)-2b(a2b-2ab+2a).
其中,a=-1,b=-2.
感悟新知
ab(ab-2a+2)-2b(a2b-2ab+2a)=ab·ab-ab·2a+ab·2-2b·a2b+2b·2ab-2b·2a=a2b2-2a2b+2ab-2a2b2+4ab2-4ab=-a2b2-2a2b+4ab2-2ab.
当a=-1,b=-2时,原式=-(-1)2×(-2)2-2×(-1)2×(-2)+4×(-1)×(-2)2-2×(-1) ×(-2)=-4+4-16-4=-20.
解:
感悟新知
3.
解方程: x(x-3)+2x(x+2)=3x2-5.
去括号,得x2-3x+2x2+4x=3x2-5.
移项,得x2-3x+2x2+4x-3x2=-5.
合并同类项,得x=-5.
解:
感悟新知
4.
计算下列物体的体积和表面积:
感悟新知
解:
圆柱:体积V=πr2·(3r+3)=3πr3+3πr2;
表面积S=2πr2+2πr(3r+3)=2πr2+6πr2+6πr=8πr2+6πr.
长方体:体积V=(4a-1)·a·2a=8a3-2a2;
表面积S=2[2a·(4a-1)+2a·a+a·(4a-1)]=2(8a2-2a+2a2+4a2-a)=2(14a2-3a)=28a2-6a.
感悟新知
5.
今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy (4y-2x-1)=-12xy2+6x2y+□,□的地方被钢笔水弄污了,你认为□内应填写( )
A.3xy B.-3xy
C.-1 D.1
A
感悟新知
6.
要使x(x+a)+3x-2b=x2+5x+4成立,则a,b的值分别为( )
A.a=-2,b=-2 B.a=2,b=2
C.a=2,b=-2 D.a=-2,b=2
若计算(x2+ax+5)·(-2x)-6x2的结果中不含有x2项,则a的值为( )
A.-3 B.-
C.0 D.3
C
A
7.
感悟新知
8.
如图,通过计算大长方形的面积可得到的恒等式为________________________.
2a(a+b)=2a2+2ab
感悟新知
9.
化简:
(1)(-2ab)(3a2-2ab-4b2);
(2)3x(2x-3y)-(2x-5y)·4x;
(3)5a(a-b+c)-2b(a+b-c)-4c(-a-b-c).
(1)原式=-6a3b+4a2b2+8ab3.
(2)原式=6x2-9xy-8x2+20xy=-2x2+11xy.
(3)原式=5a2-5ab+5ac-2ab-2b2+2bc+4ac+4bc+4c2=5a2-2b2+4c2-7ab+9ac+6bc.
解:
感悟新知
10.
解:
先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),
其中a=-2.
原式=6a3-12a2+9a-6a3-8a2=-20a2+9a,
当a=-2时,原式=-20×4-9×2=-98.
感悟新知
11.
解:
解方程:2x(x-1)=12+x(2x-5).
去括号,得2x2-2x=12+2x2-5x,
移项、合并同类项,得3x=12,
系数化为1,得x=4.
本节小结
单项式与多项
式相乘
1. 单项式与多项式相乘的依据是:乘法对加法的分配
律.
2. 单项式与多项式相乘,其积仍是多项式,项数与原
多项式的项数 相同,注意不要漏乘项.
3. 积的每一项的符号由原多项式各项符号和单项式的
符号来决定,注意去括号法则.
本节小结
单项式与多项
式相乘
下列运算中,正确的是( )
A.-2x(3x2y-2xy)=-6x3y-4x2y
B.2xy2(-x2+2y2+1)=-4x3y4
C.(3ab2-2ab)·abc=3a2b3-2a2b2
D.(ab)2(2ab2-c)=2a3b4-a2b2c
D
易错点:对单项式与多项式相乘的法则理解不透而出错
本节小结
点拨:
单项式与单项
式相乘
单项式与多项式相乘时,A中多项式的每一项都包括其前面的符号,单项式如果含有负号,运算时容易漏掉单项式的负号,或多项式中每一项的符号而产生错解.B中单项式要与多项式中的每一项相乘,不能漏项.C中单项式与单项式相乘时,对于只在一个单项式里含有的字母,容易漏掉.
请完成教材课后习题
作业提升
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
