冀教版数学七年级下册8.5.3 整式的化简 导学课件(共33张PPT)
文档属性
| 名称 | 冀教版数学七年级下册8.5.3 整式的化简 导学课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 13:03:33 | ||
图片预览










文档简介
(共33张PPT)
8.5 乘法公式
第8章 整式的乘法
第3课时 整式的化简
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
整式的化简
整式化简的实际应用
课时导入
一根钢管的横截面积如图,r表示内半径,h表示钢管的厚度. 怎样表示这根钢管的面积?
知识点
整式的化简
感悟新知
1
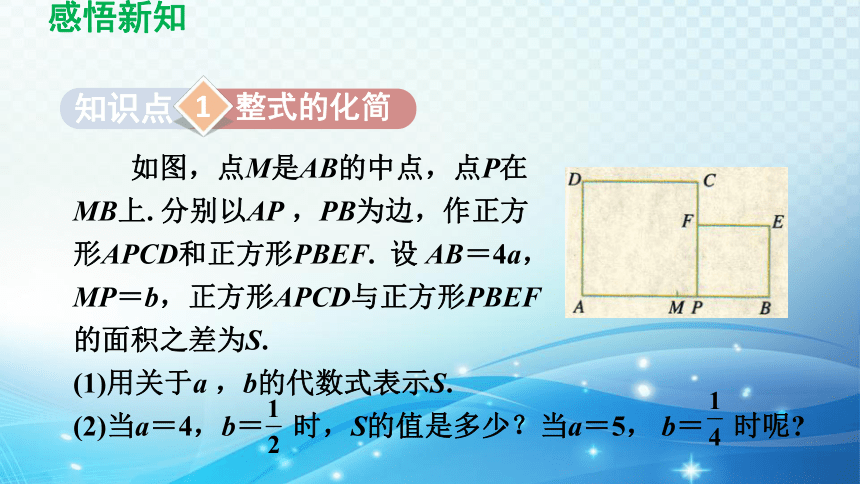
如图,点M是AB的中点,点P在
MB上. 分别以AP ,PB为边,作正方
形APCD和正方形PBEF. 设 AB=4a,
MP=b,正方形APCD与正方形PBEF
的面积之差为S.
(1)用关于a ,b的代数式表示S.
(2)当a=4,b= 时,S的值是多少?当a=5, b= 时呢
归 纳
感悟新知
整式的化简应遵循先乘方、再乘除、最后算加减
的顺序.能运用乘法公式的则运用公式.
感悟新知
1. 在运算中,经常利用整式乘法的运算法则及乘法
公式对较复杂的题目进行化简.整式的化简应遵
循先乘方、再乘除、最后算加减的顺序.能运用
乘法公式的则运用公式.
2. 易错提示:
(1)运用乘法公式时,括号前是负号的要注意变号.
(2)结果中有同类项的一定要合并同类项.
感悟新知
例 1
解:
化简:
(1)(2x-1)(2x+1)-(4x+3)(x-6).
(2)(2a+3b)2-4a(a+3b+1).
(1)(2x-1)(2x+1)-(4x+3)(x-6)
=4x2-1-(4x2-24x+3x-18)
=4x2-1-(4x2-21x-18)
= 4x2-1- 4x2+21x+18
=21x+17.
感悟新知
(2)(2a+3b)2-4a(a+3b+1)
=4a2+12ab+9b2-4a2-12ab-4a
=9b2-4a.
归 纳
感悟新知
灵活运用乘法公式是解题的关键.同时还要注意
符号问题.
感悟新知
1.
解:
计算:
(1)(x+5)2-(x-5)2 ; (2)(a+b+c)(a+b-c) ;
(3)(a+b-c)(a-b+c).
(1)(x+5)2-(x-5)2=[(x+5)+(x-5)][(x+5)-(x-5)]=2x·10=20x.
(2)(a+b+c)(a+b-c)=(a+b)2-c2=a2+2ab+b2-c2.
感悟新知
(3)(a+b-c)(a-b+c)=[a+(b-c)][a-(b-c)]=a2-(b-c)2=a2-b2+2bc-c2.
感悟新知
2.
计算:
(1)(a+b+c)2 ; (2)(a+b)2(a-b)2.
(1)(a+b+c)2=[(a+b)+c]2=(a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2ac+2bc.
(2)(a+b)2(a-b)2=[(a+b)(a-b)]2=(a2-b2)2=a4-2a2b2+b4.
解:
感悟新知
3.
下列计算正确的是( )
A.(-4x)(2x2+3x-1)=8x3-12x2-4x
B.(x+y)(x2+y2)=x3+y3
C.(-4a-1)(4a-1)=1-16a2
D.(x-2y)2=x2-2xy+4y2
C
感悟新知
4.
化简(a-1)(a+1)(a2+1)-(a4+1)的结果是( )
A.0 B.2
C.-2 D.不能确定
若代数式x2+ax+9-(x-3)2的值等于零,则a的值为( )
A.0 B.-3
C.-6 D.9
C
C
5.
感悟新知
6.
7.
已知a2+b2=25,且ab=12,则a+b的值是( )
A.±7 B.7
C.± D.
若x2+4x-4=0,则3(x-2)2-6(x+1)(x-1)的值为( )
A.-6 B.6
C.18 D.30
A
B
感悟新知
8.
当x=1时,ax+b+1的值为-2,则(a+b-1)(1-a-b)的值为( )
A.-16 B.-8
C.8 D.16
A
感悟新知
9.
若x2+ax= +b,则a,b的值是( )
A.a=1,b=
B.a=1,b=
C.a=0,b=
D.a=2,b=
B
感悟新知
知识点
整式化简的实际应用
2
例2
甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减 少x%.
(1)5月份甲超市的销售额比乙超市多多少?
(2)若a=150,x=2,则5月份甲超市的销售额比乙
超市多多少万元?
感悟新知
解:
(1)由题意,5月份甲超市的销售额为a(1+x%)2,
乙超市的销售额为a(1-x% )2,
则甲、乙两超市的销售额的差为
a(1+x%)2- a(1-x% )2
答:甲超市的销售额比乙超市多
感悟新知
(2)当a=150,x=2时,
答:甲超市的销售额比乙超市多12万元.
归 纳
感悟新知
在解答实际问题时,如果题目有字母就注意整式
的化简,化简后再代入数值.
感悟新知
1.
解:
一个正方形,如果边长增加3 m,它的面积就增加39 m2,求这个正方形的边长.
设这个正方形的边长为x m,根据题意,得(x+3)2-x2=39,
x2+6x+9-x2=39,6x=30,x=5.
答:这个正方形的边长为5 m.
感悟新知
2.
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大的圆的直径.求图中阴影部分的面积.
感悟新知
解:
直径是(m+n)的圆的面积S1=π· ,
以m为直径的圆的面积S2=π· ,以n为直径的
圆的面积S3=π· ,
则所求阴影部分的面积S=S1-S2-S3=π·
-π· -π· = - m2
- n2= - m2- n2= πmn.
感悟新知
答:图中阴影部分的面积为 πmn.
感悟新知
3.
计算(a-b)(a+b)(a2+b2)(a4-b4)的结果是( )
A.a8+2a4b4+b8
B.a8-2a4b4+b8
C.a8+b8
D.a8-b8
B
感悟新知
4.
如图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
A.2mn B.(m+n)2
C.(m-n)2 D.m2-n2
C
感悟新知
5.
已知P= m-1,Q=m2- m(m为任意数),
则P,Q的大小关系为( )
A.P<Q B.P=Q
C.P>Q D.由m的值确定
A
感悟新知
6.
某商品原价为a元,因需求量增大,经营者连续两次提价,每次提价10%,后因市场物价调整,又一次性降价20%,则降价后这种商品的价格
是( )
A.1.08a元 B.0.88a元
C.0.968a元 D.a元
C
本节小结
完全平方公式
1. 整式化简的顺序:
整式的化简应遵循先乘方、再乘除、最后算加
减的顺序.能运用乘法公式的则运用公式.
2. 列代数式的步骤:
(1)审题,理解题意;
(2)根据题目中的数量关系列出代数式;
(3)化简代数式.
本节小结
完全平方公式
化简(5x-4y)(-5x+4y)+(5x+4y)2.
(5x-4y)(-5x+4y)+(5x+4y)2
=-(5x-4y)(5x-4y)+(5x+4y)2
=-(5x-4y)2+(5x+4y)2
=-(25x2-40xy+16y2)+(25x2+40xy+16y2)
=80xy.
解:
本节小结
完全平方公式
易错点:在整式的化简中,易用错公式
本题中(5x-4y)与(-5x+4y)不符合平方差公式的特点,不能运用平方差公式化简,在提取“-”后,用完全平方公式进行化简.
易错总结:
请完成教材课后习题
作业提升
8.5 乘法公式
第8章 整式的乘法
第3课时 整式的化简
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
整式的化简
整式化简的实际应用
课时导入
一根钢管的横截面积如图,r表示内半径,h表示钢管的厚度. 怎样表示这根钢管的面积?
知识点
整式的化简
感悟新知
1
如图,点M是AB的中点,点P在
MB上. 分别以AP ,PB为边,作正方
形APCD和正方形PBEF. 设 AB=4a,
MP=b,正方形APCD与正方形PBEF
的面积之差为S.
(1)用关于a ,b的代数式表示S.
(2)当a=4,b= 时,S的值是多少?当a=5, b= 时呢
归 纳
感悟新知
整式的化简应遵循先乘方、再乘除、最后算加减
的顺序.能运用乘法公式的则运用公式.
感悟新知
1. 在运算中,经常利用整式乘法的运算法则及乘法
公式对较复杂的题目进行化简.整式的化简应遵
循先乘方、再乘除、最后算加减的顺序.能运用
乘法公式的则运用公式.
2. 易错提示:
(1)运用乘法公式时,括号前是负号的要注意变号.
(2)结果中有同类项的一定要合并同类项.
感悟新知
例 1
解:
化简:
(1)(2x-1)(2x+1)-(4x+3)(x-6).
(2)(2a+3b)2-4a(a+3b+1).
(1)(2x-1)(2x+1)-(4x+3)(x-6)
=4x2-1-(4x2-24x+3x-18)
=4x2-1-(4x2-21x-18)
= 4x2-1- 4x2+21x+18
=21x+17.
感悟新知
(2)(2a+3b)2-4a(a+3b+1)
=4a2+12ab+9b2-4a2-12ab-4a
=9b2-4a.
归 纳
感悟新知
灵活运用乘法公式是解题的关键.同时还要注意
符号问题.
感悟新知
1.
解:
计算:
(1)(x+5)2-(x-5)2 ; (2)(a+b+c)(a+b-c) ;
(3)(a+b-c)(a-b+c).
(1)(x+5)2-(x-5)2=[(x+5)+(x-5)][(x+5)-(x-5)]=2x·10=20x.
(2)(a+b+c)(a+b-c)=(a+b)2-c2=a2+2ab+b2-c2.
感悟新知
(3)(a+b-c)(a-b+c)=[a+(b-c)][a-(b-c)]=a2-(b-c)2=a2-b2+2bc-c2.
感悟新知
2.
计算:
(1)(a+b+c)2 ; (2)(a+b)2(a-b)2.
(1)(a+b+c)2=[(a+b)+c]2=(a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2ac+2bc.
(2)(a+b)2(a-b)2=[(a+b)(a-b)]2=(a2-b2)2=a4-2a2b2+b4.
解:
感悟新知
3.
下列计算正确的是( )
A.(-4x)(2x2+3x-1)=8x3-12x2-4x
B.(x+y)(x2+y2)=x3+y3
C.(-4a-1)(4a-1)=1-16a2
D.(x-2y)2=x2-2xy+4y2
C
感悟新知
4.
化简(a-1)(a+1)(a2+1)-(a4+1)的结果是( )
A.0 B.2
C.-2 D.不能确定
若代数式x2+ax+9-(x-3)2的值等于零,则a的值为( )
A.0 B.-3
C.-6 D.9
C
C
5.
感悟新知
6.
7.
已知a2+b2=25,且ab=12,则a+b的值是( )
A.±7 B.7
C.± D.
若x2+4x-4=0,则3(x-2)2-6(x+1)(x-1)的值为( )
A.-6 B.6
C.18 D.30
A
B
感悟新知
8.
当x=1时,ax+b+1的值为-2,则(a+b-1)(1-a-b)的值为( )
A.-16 B.-8
C.8 D.16
A
感悟新知
9.
若x2+ax= +b,则a,b的值是( )
A.a=1,b=
B.a=1,b=
C.a=0,b=
D.a=2,b=
B
感悟新知
知识点
整式化简的实际应用
2
例2
甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减 少x%.
(1)5月份甲超市的销售额比乙超市多多少?
(2)若a=150,x=2,则5月份甲超市的销售额比乙
超市多多少万元?
感悟新知
解:
(1)由题意,5月份甲超市的销售额为a(1+x%)2,
乙超市的销售额为a(1-x% )2,
则甲、乙两超市的销售额的差为
a(1+x%)2- a(1-x% )2
答:甲超市的销售额比乙超市多
感悟新知
(2)当a=150,x=2时,
答:甲超市的销售额比乙超市多12万元.
归 纳
感悟新知
在解答实际问题时,如果题目有字母就注意整式
的化简,化简后再代入数值.
感悟新知
1.
解:
一个正方形,如果边长增加3 m,它的面积就增加39 m2,求这个正方形的边长.
设这个正方形的边长为x m,根据题意,得(x+3)2-x2=39,
x2+6x+9-x2=39,6x=30,x=5.
答:这个正方形的边长为5 m.
感悟新知
2.
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大的圆的直径.求图中阴影部分的面积.
感悟新知
解:
直径是(m+n)的圆的面积S1=π· ,
以m为直径的圆的面积S2=π· ,以n为直径的
圆的面积S3=π· ,
则所求阴影部分的面积S=S1-S2-S3=π·
-π· -π· = - m2
- n2= - m2- n2= πmn.
感悟新知
答:图中阴影部分的面积为 πmn.
感悟新知
3.
计算(a-b)(a+b)(a2+b2)(a4-b4)的结果是( )
A.a8+2a4b4+b8
B.a8-2a4b4+b8
C.a8+b8
D.a8-b8
B
感悟新知
4.
如图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
A.2mn B.(m+n)2
C.(m-n)2 D.m2-n2
C
感悟新知
5.
已知P= m-1,Q=m2- m(m为任意数),
则P,Q的大小关系为( )
A.P<Q B.P=Q
C.P>Q D.由m的值确定
A
感悟新知
6.
某商品原价为a元,因需求量增大,经营者连续两次提价,每次提价10%,后因市场物价调整,又一次性降价20%,则降价后这种商品的价格
是( )
A.1.08a元 B.0.88a元
C.0.968a元 D.a元
C
本节小结
完全平方公式
1. 整式化简的顺序:
整式的化简应遵循先乘方、再乘除、最后算加
减的顺序.能运用乘法公式的则运用公式.
2. 列代数式的步骤:
(1)审题,理解题意;
(2)根据题目中的数量关系列出代数式;
(3)化简代数式.
本节小结
完全平方公式
化简(5x-4y)(-5x+4y)+(5x+4y)2.
(5x-4y)(-5x+4y)+(5x+4y)2
=-(5x-4y)(5x-4y)+(5x+4y)2
=-(5x-4y)2+(5x+4y)2
=-(25x2-40xy+16y2)+(25x2+40xy+16y2)
=80xy.
解:
本节小结
完全平方公式
易错点:在整式的化简中,易用错公式
本题中(5x-4y)与(-5x+4y)不符合平方差公式的特点,不能运用平方差公式化简,在提取“-”后,用完全平方公式进行化简.
易错总结:
请完成教材课后习题
作业提升
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
