浙江省余姚市提前招生考试数学试卷(附答案)
文档属性
| 名称 | 浙江省余姚市提前招生考试数学试卷(附答案) | 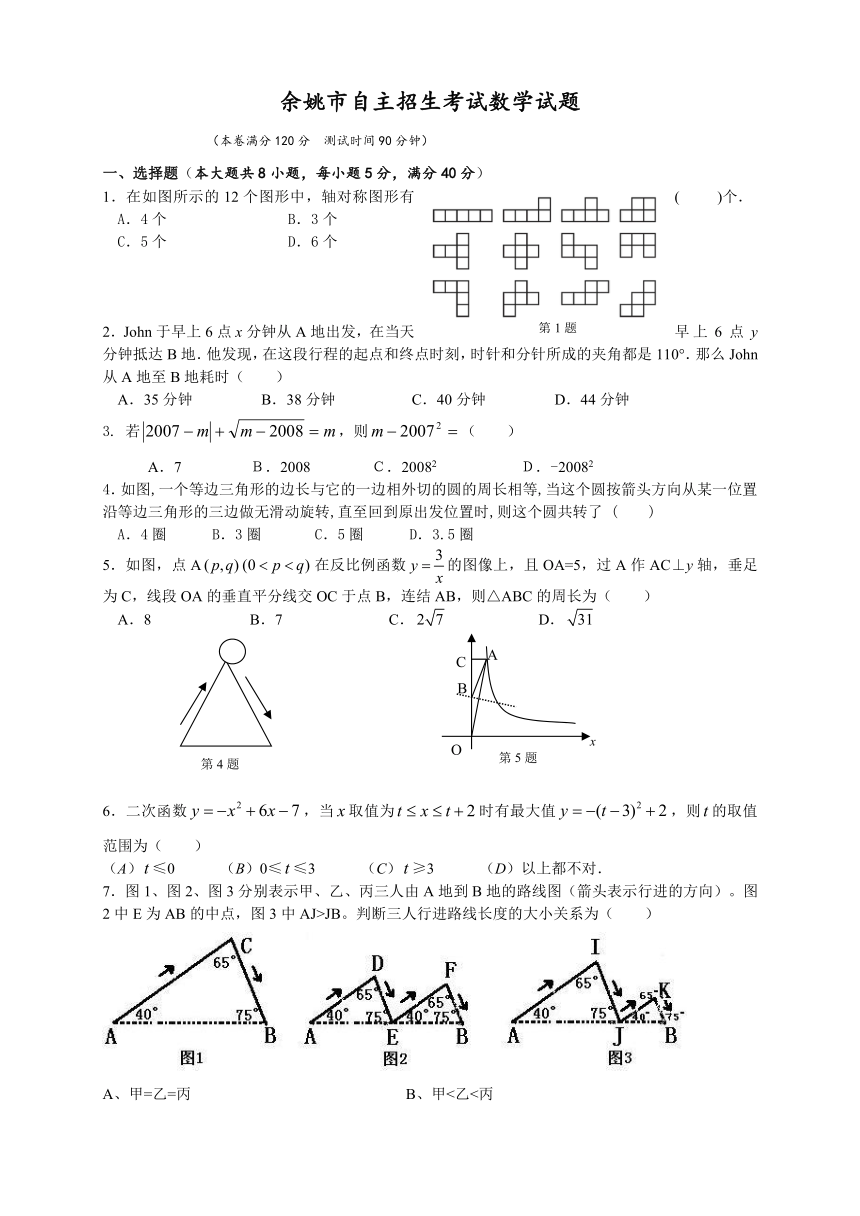 | |
| 格式 | zip | ||
| 文件大小 | 194.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-06 08:20:45 | ||
图片预览




文档简介
余姚市自主招生考试数学试题
(本卷满分120分 测试时间90分钟)
一、选择题(本大题共8小题,每小题5分,满分40分)
1.在如图所示的12个图形中,轴对称图形有( )个.
A.4个 B.3个
C.5个 D.6个
2.John于早上6点x分钟从A地出发, ( http: / / www.21cnjy.com )在当天早上6点y分钟抵达B地.他发现,在这段行程的起点和终点时刻,时针和分针所成的夹角都是110.那么John从A地至B地耗时( )
A.35分钟 B.38分钟 C.40分钟 D.44分钟
3. 若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ( )
A.7 B.2008 C.20082 D.-20082
4.如图,一个等边三角形的边长与它的一边相 ( http: / / www.21cnjy.com )外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了 ( )
A.4圈 B.3圈 C.5圈 D.3.5圈
5.如图,点A HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在反比例函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图像上,且OA=5,过A作AC⊥y轴,垂足为C,线段OA的垂直平分线交OC于点B,连结AB,则△ABC的周长为( )
A.8 B.7 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
6.二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 取值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时有最大值 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围为( )
(A) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤0 (B)0≤ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤3 (C) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≥3 (D)以上都不对.
7.图1、图2、图3分别表示甲、乙、丙三人 ( http: / / www.21cnjy.com )由A地到B地的路线图(箭头表示行进的方向)。图2中E为AB的中点,图3中AJ>JB。判断三人行进路线长度的大小关系为( )
( http: / / www.21cnjy.com )
A、甲=乙=丙 B、甲<乙<丙
C、乙<丙<甲 D、丙<乙<甲
8.P是△ABC内一点,AD、BE、CF过点P并且交边BC、CA、AB于D、E、F,则 HYPERLINK "http://www.21cnjy.com"
A 1 B 2 C 3 D 4
二、填空题(本大题共7小题,每小题4分,共28分)
9.若2x+5y-5=0,则4x×32y=______________
10.记 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
11.圆内接四边形四条边长顺次为5、10、11、14;则这个四边形的面积为
12.如图, HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 分别是 HYPERLINK "http://www.21cnjy.com" 的边 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 上的点, HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 相交于点 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 相交于点 HYPERLINK "http://www.21cnjy.com" ,若 HYPERLINK "http://www.21cnjy.com" △APD HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" △BQC HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" ,则阴影部分的面积为 HYPERLINK "http://www.21cnjy.com" .
13若ax2+(a+2)x+9a=0有两个不同实根,x1,x2,且x1<214.如图,正方形 HYPERLINK "http://www.21cnjy.com" 的边长为1, HYPERLINK "http://www.21cnjy.com" 为 HYPERLINK "http://www.21cnjy.com" 所在直线上的两点,且 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,则四边形 HYPERLINK "http://www.21cnjy.com" 的面积为___________
15.方程x2+2x-1= ( http: / / www.21cnjy.com )0的解可视为函数y=x+2的图象与函数y=的图象交点的横坐标,那么方程kx2+x-4=0的两个解其实就是直线 ▲ 与双曲线 ▲ 图象交点的横坐标,若这两个交点均在直线y=x的同侧,则实数k的取值范围是 .
三、解答题(本大题共5小题,第16-19题各10分,第20题12分,共52分)
16.(1)已知非零实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
(2)已知实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
17.如图,在等腰三角形ABC中,AB=1,∠A=900,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积。
18.在代数学中,为了表述的简洁,常用记号 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,… 来表示以x为自变量的函数.例如,若用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 来表示二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;而 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示自变量x取值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时的函数值,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
另外,我们把形如 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
(其中 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为系数,x为变量)的函数称为关于x的一元n次多项式.
已知关于x的实系数多项式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足:对任意实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,以下两式恒成立.
(ⅰ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ; (ⅱ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
试解答如下两个问题:
(1)证明:函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是一次函数; (2)求函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的表达式.
19.设抛物线 HYPERLINK "http://www.21cnjy.com" 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线 HYPERLINK "http://www.21cnjy.com" 交抛物线于另一点E. 若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BD ( http: / / www.21cnjy.com )P的外接圆半径等于________________.
HYPERLINK "http://www.21cnjy.com"
20.在ΔABC中,AB=AC,BC=6,sinB= HYPERLINK "http://www.21cnjy.com" ,点P从点B出发沿射线BA移动,同时点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图(1),当点P为AB的中点时,求CD的长;
(2)如图(2),过点P作直线BC ( http: / / www.21cnjy.com )的垂线,垂足为点E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段 请说明理由;
(3)如图(3),当PQ经过ΔABC的重心G时,求BP的长.
2012年
余姚市自主招生考试数学答题卷
(本卷满分120分 测试时间90分钟) 姓名 学号
一、选择题(本大题共8小题,每小题5分,满分40分)
题号 1 2 3 4 5 6 7 8
答案
二、填空题(本大题共7小题,每小题4分,共28分)
9. 10.
11. 12.
13. 14.
15.
三、解答题(本大题共5小题,第16、17、18、19题各10分,第20题12分,共52分)
16.(1)已知非零实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
(2)已知实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
17.如图,在等腰三角形ABC中,AB=1,∠A=900,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积。
18.在代数学中,为了表述的简洁,常用记号 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,… 来表示以x为自变量的函数.例如,若用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 来表示二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;而 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示自变量x取值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时的函数值,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
另外,我们把形如 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
(其中 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为系数,x为变量)的函数称为关于x的一元n次多项式.
已知关于x的实系数多项式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足:对任意实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,以下两式恒成立.
(ⅰ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ; (ⅱ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
试解答如下两个问题:
(1)证明:函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是一次函数; (2)求函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的表达式.
19. 设抛物线 HYPERLINK "http://www.21cnjy.com" 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线 HYPERLINK "http://www.21cnjy.com" 交抛物线于另一点E. 若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△ ( http: / / www.21cnjy.com )BDP的外接圆半径等于________________.
HYPERLINK "http://www.21cnjy.com"
20. (本题满分12分)在ΔABC中,AB=AC,BC=6,sinB= HYPERLINK "http://www.21cnjy.com" ,点P从点B出发沿射线BA移动,同时点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图(1),当点P为AB的中点时,求CD的长;
(2)如图(2),过点P作直线BC的垂线,垂 ( http: / / www.21cnjy.com )足为点E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段 请说明理由;
(3)如图(3),当PQ经过ΔABC的重心G时,求BP的长.
余姚市自主招生考试数学参考答案
(本卷满分120分 测试时间90分钟)
一、选择题(本大题共8小题,每小题5分,满分40分)
题号 1 2 3 4 5 6 7 8
答案 D C B A D C A
二、填空题(本大题共7小题,每小题4分,共28分)
9. 32 10. HYPERLINK "http://www.21cnjy.com"
11. 90 12. 40
13. -4/15小于a小于0 14. HYPERLINK "http://www.21cnjy.com"
15. HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
三、解答题(本大题共5小题,第16、17、18、19题各10分,第20题12分,共52分)
16.解:
(1)由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , ………………2分
将b消去可得, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………4分
HYPERLINK "http://www.21cnjy.com" ………………5分
(2)依题意得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………7分
对等式两端分别平方可得
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
将两式的左右对应相加可得
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………9分
即知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………10分
17. 解法1:如图,过C作CD⊥CE与EF的延长线交于D.因为∠ABE+∠AEB=90°,
∠CED+∠AEB=90°,所以 ∠ABE=∠CED.于是Rt△ABE∽Rt△CED,所以
HYPERLINK "http://www.21cnjy.com" ………………4分
又∠ECF=∠DCF=45°,所以CF是∠DCE的平分线,点F到CE和CD的距离相等,所以
HYPERLINK "http://www.21cnjy.com" ………………8分 HYPERLINK "http://www.21cnjy.com" …………10分
(解法2: 如图3-278,作FH⊥CE于H)
18. 解:(1)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (c为常数),则在(ⅰ)式中令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 可得,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………4分
以x代y,即知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .所以函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是一次函数. ………………5分
(2)由(ⅰ)式知, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ……6分
代入(ⅱ)式得到, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
对任意实数恒成立. ………………8分
因此, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
但同时注意到 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,经检验符合题意. ………………10分
19.解答:21、(1).M=4,y=1/2x -3/2x-2………………2分
(2)p1(13/7,0) p2(-22/5,0) ………………6分
(3)3 HYPERLINK "http://www.21cnjy.com" /14或3 HYPERLINK "http://www.21cnjy.com" /5………………10分
20.(1)过点P作PF∥AC交BC于F,∵P为AB的中点, F为BC的中点,∴FC=3,可证ΔPFD≌ΔQCD得DC=FD= HYPERLINK "http://www.21cnjy.com" ------2分.
(2) 当点P、Q在移动的过程中,线段DE的长度保持不变.-----3分
①如果点P在线段AB上时,过点P作PF∥AC交BC于F,由AB=AC,可证PB=PF,
∵PE⊥BC,∴BE=FE,再证ΔPFD≌ΔQCD得DC=FD,∴ED= HYPERLINK "http://www.21cnjy.com" BC=3-----5分.
②如果点P在线段BA的延长线上时,同理可得ED=3------6分.
∴当点P、Q在移动的过程中,线段DE的长度保持不变-------7分.
(3)作PE⊥BC于点E,连结AG并延长交BC于点H,∵AB=AC,G为ΔABC的重心,∴AH⊥BC,BH=CH=3,由sinB= HYPERLINK "http://www.21cnjy.com" ,得AH=4,GH= HYPERLINK "http://www.21cnjy.com" ---9分
设BP= HYPERLINK "http://www.21cnjy.com" ,则PE= HYPERLINK "http://www.21cnjy.com" ,BE= HYPERLINK "http://www.21cnjy.com" ,∵ BH= ED=3,∴HD=BE= HYPERLINK "http://www.21cnjy.com" ---10分,
由ΔDGH∽ΔDPE得 HYPERLINK "http://www.21cnjy.com" ,即 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" ,BP= HYPERLINK "http://www.21cnjy.com" .
………………12分
第1题
x
O
A
C
B
第5题
第4题
(第14题)
P
A
B
C
D
E
F
Q
(第12题)
(本卷满分120分 测试时间90分钟)
一、选择题(本大题共8小题,每小题5分,满分40分)
1.在如图所示的12个图形中,轴对称图形有( )个.
A.4个 B.3个
C.5个 D.6个
2.John于早上6点x分钟从A地出发, ( http: / / www.21cnjy.com )在当天早上6点y分钟抵达B地.他发现,在这段行程的起点和终点时刻,时针和分针所成的夹角都是110.那么John从A地至B地耗时( )
A.35分钟 B.38分钟 C.40分钟 D.44分钟
3. 若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 ( )
A.7 B.2008 C.20082 D.-20082
4.如图,一个等边三角形的边长与它的一边相 ( http: / / www.21cnjy.com )外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了 ( )
A.4圈 B.3圈 C.5圈 D.3.5圈
5.如图,点A HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在反比例函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图像上,且OA=5,过A作AC⊥y轴,垂足为C,线段OA的垂直平分线交OC于点B,连结AB,则△ABC的周长为( )
A.8 B.7 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
6.二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 取值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时有最大值 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围为( )
(A) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤0 (B)0≤ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤3 (C) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≥3 (D)以上都不对.
7.图1、图2、图3分别表示甲、乙、丙三人 ( http: / / www.21cnjy.com )由A地到B地的路线图(箭头表示行进的方向)。图2中E为AB的中点,图3中AJ>JB。判断三人行进路线长度的大小关系为( )
( http: / / www.21cnjy.com )
A、甲=乙=丙 B、甲<乙<丙
C、乙<丙<甲 D、丙<乙<甲
8.P是△ABC内一点,AD、BE、CF过点P并且交边BC、CA、AB于D、E、F,则 HYPERLINK "http://www.21cnjy.com"
A 1 B 2 C 3 D 4
二、填空题(本大题共7小题,每小题4分,共28分)
9.若2x+5y-5=0,则4x×32y=______________
10.记 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
11.圆内接四边形四条边长顺次为5、10、11、14;则这个四边形的面积为
12.如图, HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 分别是 HYPERLINK "http://www.21cnjy.com" 的边 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 上的点, HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 相交于点 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 相交于点 HYPERLINK "http://www.21cnjy.com" ,若 HYPERLINK "http://www.21cnjy.com" △APD HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" △BQC HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" ,则阴影部分的面积为 HYPERLINK "http://www.21cnjy.com" .
13若ax2+(a+2)x+9a=0有两个不同实根,x1,x2,且x1<2
15.方程x2+2x-1= ( http: / / www.21cnjy.com )0的解可视为函数y=x+2的图象与函数y=的图象交点的横坐标,那么方程kx2+x-4=0的两个解其实就是直线 ▲ 与双曲线 ▲ 图象交点的横坐标,若这两个交点均在直线y=x的同侧,则实数k的取值范围是 .
三、解答题(本大题共5小题,第16-19题各10分,第20题12分,共52分)
16.(1)已知非零实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
(2)已知实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
17.如图,在等腰三角形ABC中,AB=1,∠A=900,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积。
18.在代数学中,为了表述的简洁,常用记号 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,… 来表示以x为自变量的函数.例如,若用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 来表示二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;而 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示自变量x取值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时的函数值,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
另外,我们把形如 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
(其中 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为系数,x为变量)的函数称为关于x的一元n次多项式.
已知关于x的实系数多项式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足:对任意实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,以下两式恒成立.
(ⅰ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ; (ⅱ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
试解答如下两个问题:
(1)证明:函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是一次函数; (2)求函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的表达式.
19.设抛物线 HYPERLINK "http://www.21cnjy.com" 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线 HYPERLINK "http://www.21cnjy.com" 交抛物线于另一点E. 若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BD ( http: / / www.21cnjy.com )P的外接圆半径等于________________.
HYPERLINK "http://www.21cnjy.com"
20.在ΔABC中,AB=AC,BC=6,sinB= HYPERLINK "http://www.21cnjy.com" ,点P从点B出发沿射线BA移动,同时点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图(1),当点P为AB的中点时,求CD的长;
(2)如图(2),过点P作直线BC ( http: / / www.21cnjy.com )的垂线,垂足为点E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段 请说明理由;
(3)如图(3),当PQ经过ΔABC的重心G时,求BP的长.
2012年
余姚市自主招生考试数学答题卷
(本卷满分120分 测试时间90分钟) 姓名 学号
一、选择题(本大题共8小题,每小题5分,满分40分)
题号 1 2 3 4 5 6 7 8
答案
二、填空题(本大题共7小题,每小题4分,共28分)
9. 10.
11. 12.
13. 14.
15.
三、解答题(本大题共5小题,第16、17、18、19题各10分,第20题12分,共52分)
16.(1)已知非零实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
(2)已知实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
17.如图,在等腰三角形ABC中,AB=1,∠A=900,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积。
18.在代数学中,为了表述的简洁,常用记号 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,… 来表示以x为自变量的函数.例如,若用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 来表示二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;而 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示自变量x取值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时的函数值,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
另外,我们把形如 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
(其中 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为系数,x为变量)的函数称为关于x的一元n次多项式.
已知关于x的实系数多项式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 满足:对任意实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,以下两式恒成立.
(ⅰ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ; (ⅱ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
试解答如下两个问题:
(1)证明:函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是一次函数; (2)求函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的表达式.
19. 设抛物线 HYPERLINK "http://www.21cnjy.com" 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线 HYPERLINK "http://www.21cnjy.com" 交抛物线于另一点E. 若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△ ( http: / / www.21cnjy.com )BDP的外接圆半径等于________________.
HYPERLINK "http://www.21cnjy.com"
20. (本题满分12分)在ΔABC中,AB=AC,BC=6,sinB= HYPERLINK "http://www.21cnjy.com" ,点P从点B出发沿射线BA移动,同时点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图(1),当点P为AB的中点时,求CD的长;
(2)如图(2),过点P作直线BC的垂线,垂 ( http: / / www.21cnjy.com )足为点E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段 请说明理由;
(3)如图(3),当PQ经过ΔABC的重心G时,求BP的长.
余姚市自主招生考试数学参考答案
(本卷满分120分 测试时间90分钟)
一、选择题(本大题共8小题,每小题5分,满分40分)
题号 1 2 3 4 5 6 7 8
答案 D C B A D C A
二、填空题(本大题共7小题,每小题4分,共28分)
9. 32 10. HYPERLINK "http://www.21cnjy.com"
11. 90 12. 40
13. -4/15小于a小于0 14. HYPERLINK "http://www.21cnjy.com"
15. HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
三、解答题(本大题共5小题,第16、17、18、19题各10分,第20题12分,共52分)
16.解:
(1)由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , ………………2分
将b消去可得, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………4分
HYPERLINK "http://www.21cnjy.com" ………………5分
(2)依题意得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………7分
对等式两端分别平方可得
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
将两式的左右对应相加可得
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………9分
即知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………10分
17. 解法1:如图,过C作CD⊥CE与EF的延长线交于D.因为∠ABE+∠AEB=90°,
∠CED+∠AEB=90°,所以 ∠ABE=∠CED.于是Rt△ABE∽Rt△CED,所以
HYPERLINK "http://www.21cnjy.com" ………………4分
又∠ECF=∠DCF=45°,所以CF是∠DCE的平分线,点F到CE和CD的距离相等,所以
HYPERLINK "http://www.21cnjy.com" ………………8分 HYPERLINK "http://www.21cnjy.com" …………10分
(解法2: 如图3-278,作FH⊥CE于H)
18. 解:(1)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (c为常数),则在(ⅰ)式中令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 可得,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ………………4分
以x代y,即知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .所以函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是一次函数. ………………5分
(2)由(ⅰ)式知, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ……6分
代入(ⅱ)式得到, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
对任意实数恒成立. ………………8分
因此, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
但同时注意到 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,经检验符合题意. ………………10分
19.解答:21、(1).M=4,y=1/2x -3/2x-2………………2分
(2)p1(13/7,0) p2(-22/5,0) ………………6分
(3)3 HYPERLINK "http://www.21cnjy.com" /14或3 HYPERLINK "http://www.21cnjy.com" /5………………10分
20.(1)过点P作PF∥AC交BC于F,∵P为AB的中点, F为BC的中点,∴FC=3,可证ΔPFD≌ΔQCD得DC=FD= HYPERLINK "http://www.21cnjy.com" ------2分.
(2) 当点P、Q在移动的过程中,线段DE的长度保持不变.-----3分
①如果点P在线段AB上时,过点P作PF∥AC交BC于F,由AB=AC,可证PB=PF,
∵PE⊥BC,∴BE=FE,再证ΔPFD≌ΔQCD得DC=FD,∴ED= HYPERLINK "http://www.21cnjy.com" BC=3-----5分.
②如果点P在线段BA的延长线上时,同理可得ED=3------6分.
∴当点P、Q在移动的过程中,线段DE的长度保持不变-------7分.
(3)作PE⊥BC于点E,连结AG并延长交BC于点H,∵AB=AC,G为ΔABC的重心,∴AH⊥BC,BH=CH=3,由sinB= HYPERLINK "http://www.21cnjy.com" ,得AH=4,GH= HYPERLINK "http://www.21cnjy.com" ---9分
设BP= HYPERLINK "http://www.21cnjy.com" ,则PE= HYPERLINK "http://www.21cnjy.com" ,BE= HYPERLINK "http://www.21cnjy.com" ,∵ BH= ED=3,∴HD=BE= HYPERLINK "http://www.21cnjy.com" ---10分,
由ΔDGH∽ΔDPE得 HYPERLINK "http://www.21cnjy.com" ,即 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" ,BP= HYPERLINK "http://www.21cnjy.com" .
………………12分
第1题
x
O
A
C
B
第5题
第4题
(第14题)
P
A
B
C
D
E
F
Q
(第12题)
同课章节目录
