-2022-2023学年人教版七年级数学下册5.3.1平行线的性质第一课时 教学课件(共37张PPT)
文档属性
| 名称 | -2022-2023学年人教版七年级数学下册5.3.1平行线的性质第一课时 教学课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 722.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
第五章 相交线平行线
第一课时
5.3.1 平行线的性质
【学习目标】
【学习重点】
1.掌握平行线的三条性质.
2.能初步利用平行线的性质进行有关角的计算和证明.
能区分平行线的性质和判定方法以及它们的混合应用.
平行线的三个性质和应用.
【学习难点】
复习旧知 引入新课
方法4:如果两条直线都与第三
条直线平行,那么这两
条直线也互相平行.
平行线的判定方法有哪三种?
它们是先知道什么……
后得到什么?
两直线平行
1.同位角
3.同旁内角
复习回顾
相等
互补
相等
还有其他方法吗?
2.内错角
利用同位角相等,或者内错角相等,或者同旁内角互补可以判定两条直线平行.反过来如果两条直线平行,同位角、内错角、同旁内角的数量关系又该如何表达呢?
反过来说也对吗?
合作交流 探索新知
117°
a
b
1
2
58°
82°
117°
∠1=∠2
c
58°
82°
1
2
1
2
探索新知
已知直线a,画直线b,使b∥a.
1
任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?
2
旋转截线c,同位角∠1与∠2的大小关系又如何?
3
1
两条平行线被第三条直线所截,同位角相等.
2
a
b
简单说成:
两直线平行,同位角相等.
c
通过上面的实验测量,可以得到性质1(公理):
平行线的性质一
∵ a∥b (已知),
∴ ∠1=∠2 (两直线平行,同位角相等).
符号表达:
∠1=∠2,理由如下:
a
b
c
1
2
3
∵ a∥b(已知),
如果直线a∥b,那么内错角∠2与∠3有什么关系?为什么?
又∵ ∠1=∠3(对顶角相等),
探索新知
∴ ∠2=∠3(等量代换).
∴ ∠1=∠2(两直线平行,同位角相等).
∵ a∥b (已知),
由此得到性质二
简单说成:两直线平行,内错角相等.
两条平行线被第三条直线所截,内错角相等.
3
2
a
b
c
符号表达:
∴ ∠2=∠3(两直线平行,内错角相等).
a
b
c
1
2
3
4
∠2+∠4=180°理由如下:
∵ a∥b(已知),
又∵ ∠1+∠4=180°(邻补角定义),
如果直线a∥b,那么同旁内角∠2与∠4有什么关系?为什么?
探索新知
∴ ∠1=∠2(两直线平行,同位角相等).
∴ ∠2+∠4=180°(等量代换).
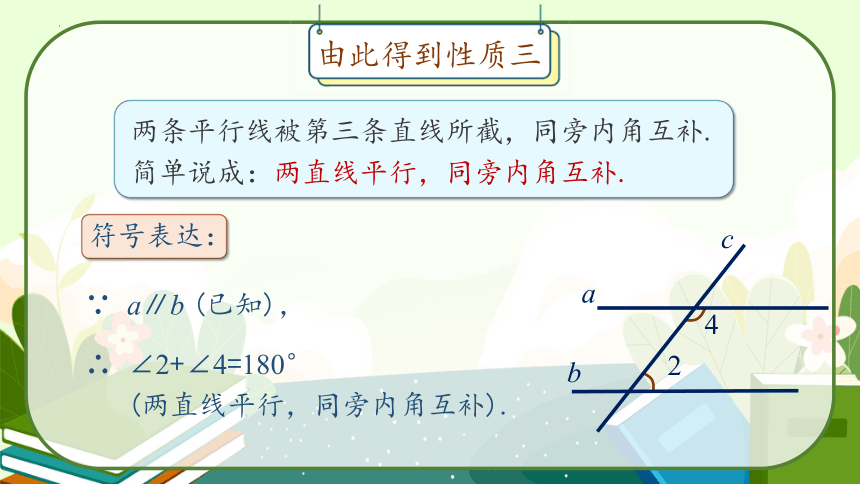
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∵ a∥b (已知),
由此得到性质三
4
2
a
b
c
符号表达:
∴ ∠2+∠4=180°
(两直线平行,同旁内角互补).
d
平行线的性质一(公理)
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
平行线的性质二
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
精彩回放
平行线的性质三
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
应用迁移 巩固提高
如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵∠2=∠1
(对顶角相等),
∴∠2=54°
∵a∥b (已知),
∴∠4=∠1=54°
∴∠2+∠3=180°
∴∠3=180°-∠2=180°-54°=126°.
(两直线平行,同位角相等).
(两直线平行,同旁内角互补).
∠1=54°(已知),
1
2
3
4
a
b
∵a∥b(已知),
(等量代换).
例1
A
B
C
D
解:∵AD∥BC (已知),
∴ A+ B=180°
(两直线平行,同旁内角互补).
即 ∠B=180°- A=180°-115°=65°.
∵AD∥BC(已知),
∴ D+ C=180°(两直线平行,同旁内角互补).
即 C=180°- D=180°-100°=80°.
∴梯形的另外两个角分别为65°、80°.
例2
如图有一块梯形的玻璃,已知量得∠A=115°,∠D=100°, 请你想一想,梯形的另外两个角各是多少度
例3
如图,已知AD⊥BC于点D,EG⊥BC于点G,且∠E=∠3,
试说明:AD平分∠BAC.
∵ AD⊥BC, EG⊥BC(已知),
证明:
∴ AD∥EG(垂直于同一条直线的两条直线平行).
∴ ∠1=∠3(两直线平行,内错角相等).
∠2=∠E(两直线平行,同位角相等).
∵ ∠E=∠3(已知),
∴ ∠1=∠2(等量代换).
即AD平分∠BAC.
A
B
C
D
F
E
1
2
3
G
随堂练习 巩固新知
① 两直线被第三条直线所截,同位角相等.
1.判断下列语句是否正确
练一练
② 两直线平行,同旁内角相等.
③“内错角相等,两直线平行”是平行线的性质.
④“两直线平行,同旁内角互补”是平行线的性质.
2.(2019 新抚区期末)如图,a∥b,a,b被直线c
所截,若∠1=140°,则∠2=( )
A.40° B.50°
C.60° D.70°
A
3.(2019 天心区校级期中)如图所示,AB∥CD ,
DB⊥BC于点B,若∠2=50°,则∠1=( )
A.40° B.50°
C.45° D.60°
A
a
b
c
1
2
A
B
C
D
1
2
4.如图,直线AB∥CD,BE平分∠ABC,交CD于
点D,∠CDB=30°,那么∠C的度数为 .
120°
5.如图,将一张长方形纸片ABCD沿BE折叠,若
∠CBA′ =40°,则∠BEA′ = .
65°
A
B
C
D
E
A'
A
B
C
D
E
由折叠的性质知,折叠后形成的图形全等,因此∠ABE=∠A′BE.再根据平行线的性质即可求得此题.
分析
6.如图,如果AB∥CD,那么 .(至少填三种)
B
1
4
3
2
6
5
F
E
D
C
A
8
7
从同位角的角度考虑
∠1=∠3、∠2=∠4、∠5=∠7、∠6=∠8.
从内错角的角度考虑
∠2=∠7、∠3=∠6.
从同旁内角的角度考虑
∠2+∠3=180°、∠6+∠7=180°.
B
C
A
D
解:∵ AB∥CD(已知),
∴ ∠B=∠C(两直线平行,内错角相等).
又∵ ∠B= 140 °(已知),
∴ ∠C=∠B= 140 °(等量代换).
7.一自行车运动员在一条公路上骑车,两次拐弯后,和原
来的方向相同(即拐弯前后的两条路互相平行),若测
得第一次拐弯的∠B是140°,则第二次拐弯的∠C应是
多少度才合理?为什么?
∴ ∠EFB=∠C=125°
(两直线平行,同位角相等).
8.如图,已知AB∥CD,∠C=125°,
∠A=45°,求∠E的度数.
解:∵ AB∥CD,∠C=125°(已知),
∵ ∠EFA =180°-∠EFB=180°-(∠A+∠E ),
∴ ∠EFB=∠A+∠E(等量代换).
由∵ ∠A=45°,
∴ ∠E=125°-45°=80°.
A
B
C
D
E
F
当堂检测 及时反馈
1.如图,一个含有30°角的直角三角
板的两个顶点分别放在一个长方形的对边上,如果
∠1=25°,那么∠2的度数是( )
A.100° B.105°
C.115° D.120°
C
2.如图,直线a∥b,若∠1是∠2
的2倍,则∠2的度数是( )
A.30° B.60°
C.90° D.120°
B
1
2
1
2
a
b
c
3.一副三角板按如下图放置,下列结论:①∠1=∠3;②若BC∥AD,则
∠4=∠3;③若∠2=15°必有∠4=2∠D;④若
∠2=30°,则有AC∥DE,其中正确的有( )
A.②④ B.①④
C.①②④ D.①③④
D
1
B
2
3
4
A
C
D
E
4.(2019 东西湖区期中)如图1,∠DEF=20°,将长方形纸
片ABCD沿直线EF折叠成图2,再沿折痕为BF折叠成图3,
则∠CFE的度数为( )
A.100° B.120° C.140° D.160°
B
A
E
D
A
E
A
E
D
C
F
B
C
B
C
F
B
G
D
F
G
图1
图2
图3
根据两直线平行,同旁内角互补可得∠CFE =180°-∠DEF,然后得出图2中∠CFE度数;再根据两直线平行,内错角相等可得∠BFE=∠DEF ,然后求出图2中∠BFC ,再根据翻折的性质可得∠CFE +∠BFE=∠BFC ,然后代入数据计算即可得解.
【分析】
5.把一块直尺与一块三角板如图
放置,若∠1=44°,则∠2的
度数是 .
134°
6.(2018·昆明禄劝期末)如图,∠1=∠2=∠3=50°。
则∠4 的度数是 .
130°
【易错提醒】利用平行线的性质和判定时,一定要清楚由角的关系推出平性关系是平行线的判定,由平行关系得到角的关系是平行线的性质.
4
3
1
2
1
4
3
2
①DE、BC平行吗?为什么?
②∠C等于多少度?为什么?
A
C
B
E
D
解:① DE∥BC.
∴ ∠C=∠AED(两直线平行,同位角相等).
∴ ∠ADE=∠B.
∴ DE∥BC(同位角相等,两直线平行).
② 由①得DE∥BC ,
又∵∠AED=80°(已知),
∴∠C=80°(等量代换).
7.如图,已知D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=80°.
∵ ∠ADE=60°,∠B=60°,
拓展提升 能力提升
1.如图所示,已知∠1=∠2,∠C=∠D, 试说明∠A=∠F.
∴ ∠4=∠C (两直线平行,同位角相等).
∵ ∠C=∠D (已知),
A
B
C
D
E
F
1
4
3
2
解:∵ ∠1=∠2 (已知),∠3=∠2(对顶角相等),
∴ ∠1=∠3 (等量代换).
∴ DB∥EC(同位角相等,两直线平行).
∴ ∠4=∠D(等量代换).
∴ DF∥AC(内错角相等,两直线平行).
∴ ∠A=∠F (两直线平行,内错角相等).
2.(2019 义安区期末)已知:如图,点C在∠AOB的一边OA上,
过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.
解:(1)∵ 直线DE∥OB,CF平分∠ACD,
∠O=40°,
∴ ∠ECF=∠ECA+∠ACF=40°+70°=110°;
∴ ∠ACE=40°,
∴ ∠ACD=140°,
∴ ∠ACF=70°,
∴ ∠ACE=∠O,∠ACF=∠FCD,
A
E
O
G
D
F
C
B
2.(2019 义安区期末)已知:如图,点C在∠AOB的一边OA上,
过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.
(2)证明:∵ CF平分∠ACD,CG⊥CF,
∠ACD+∠OCD=180°,
∴∠FCD+∠DCG=90°,∠ACF+∠OCG=90°,
∴∠DCG=∠OCG,
∴CG平分∠OCD.
∴∠ACF=∠FCD,∠FCG=90°,
A
E
O
G
D
F
C
B
总结反思 知识内化
图形
已知
结果
结论
同位角
内错角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
a
b
c
c
c
a//b
同位角相等.
两直线平行,
a//b
两直线平行,
内错角相等.
同旁内角互补.
a//b
两直线平行,
同旁内角
∠1=∠2
∠3=∠2
∠2=∠4=180°
∠2与∠4互补
平行线的性质
2.由 得到 的结论是 .
1.由 得到 的结论是 .
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
判定
请注意:
角的关系
两直线平行
用途:
证平行
两直线平行
角相等或互补
用途:
证角相等或互补
平行线的判定
平行线的性质
小结
性质
第五章 相交线平行线
第一课时
5.3.1 平行线的性质
【学习目标】
【学习重点】
1.掌握平行线的三条性质.
2.能初步利用平行线的性质进行有关角的计算和证明.
能区分平行线的性质和判定方法以及它们的混合应用.
平行线的三个性质和应用.
【学习难点】
复习旧知 引入新课
方法4:如果两条直线都与第三
条直线平行,那么这两
条直线也互相平行.
平行线的判定方法有哪三种?
它们是先知道什么……
后得到什么?
两直线平行
1.同位角
3.同旁内角
复习回顾
相等
互补
相等
还有其他方法吗?
2.内错角
利用同位角相等,或者内错角相等,或者同旁内角互补可以判定两条直线平行.反过来如果两条直线平行,同位角、内错角、同旁内角的数量关系又该如何表达呢?
反过来说也对吗?
合作交流 探索新知
117°
a
b
1
2
58°
82°
117°
∠1=∠2
c
58°
82°
1
2
1
2
探索新知
已知直线a,画直线b,使b∥a.
1
任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?
2
旋转截线c,同位角∠1与∠2的大小关系又如何?
3
1
两条平行线被第三条直线所截,同位角相等.
2
a
b
简单说成:
两直线平行,同位角相等.
c
通过上面的实验测量,可以得到性质1(公理):
平行线的性质一
∵ a∥b (已知),
∴ ∠1=∠2 (两直线平行,同位角相等).
符号表达:
∠1=∠2,理由如下:
a
b
c
1
2
3
∵ a∥b(已知),
如果直线a∥b,那么内错角∠2与∠3有什么关系?为什么?
又∵ ∠1=∠3(对顶角相等),
探索新知
∴ ∠2=∠3(等量代换).
∴ ∠1=∠2(两直线平行,同位角相等).
∵ a∥b (已知),
由此得到性质二
简单说成:两直线平行,内错角相等.
两条平行线被第三条直线所截,内错角相等.
3
2
a
b
c
符号表达:
∴ ∠2=∠3(两直线平行,内错角相等).
a
b
c
1
2
3
4
∠2+∠4=180°理由如下:
∵ a∥b(已知),
又∵ ∠1+∠4=180°(邻补角定义),
如果直线a∥b,那么同旁内角∠2与∠4有什么关系?为什么?
探索新知
∴ ∠1=∠2(两直线平行,同位角相等).
∴ ∠2+∠4=180°(等量代换).
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∵ a∥b (已知),
由此得到性质三
4
2
a
b
c
符号表达:
∴ ∠2+∠4=180°
(两直线平行,同旁内角互补).
d
平行线的性质一(公理)
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
平行线的性质二
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
精彩回放
平行线的性质三
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
应用迁移 巩固提高
如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵∠2=∠1
(对顶角相等),
∴∠2=54°
∵a∥b (已知),
∴∠4=∠1=54°
∴∠2+∠3=180°
∴∠3=180°-∠2=180°-54°=126°.
(两直线平行,同位角相等).
(两直线平行,同旁内角互补).
∠1=54°(已知),
1
2
3
4
a
b
∵a∥b(已知),
(等量代换).
例1
A
B
C
D
解:∵AD∥BC (已知),
∴ A+ B=180°
(两直线平行,同旁内角互补).
即 ∠B=180°- A=180°-115°=65°.
∵AD∥BC(已知),
∴ D+ C=180°(两直线平行,同旁内角互补).
即 C=180°- D=180°-100°=80°.
∴梯形的另外两个角分别为65°、80°.
例2
如图有一块梯形的玻璃,已知量得∠A=115°,∠D=100°, 请你想一想,梯形的另外两个角各是多少度
例3
如图,已知AD⊥BC于点D,EG⊥BC于点G,且∠E=∠3,
试说明:AD平分∠BAC.
∵ AD⊥BC, EG⊥BC(已知),
证明:
∴ AD∥EG(垂直于同一条直线的两条直线平行).
∴ ∠1=∠3(两直线平行,内错角相等).
∠2=∠E(两直线平行,同位角相等).
∵ ∠E=∠3(已知),
∴ ∠1=∠2(等量代换).
即AD平分∠BAC.
A
B
C
D
F
E
1
2
3
G
随堂练习 巩固新知
① 两直线被第三条直线所截,同位角相等.
1.判断下列语句是否正确
练一练
② 两直线平行,同旁内角相等.
③“内错角相等,两直线平行”是平行线的性质.
④“两直线平行,同旁内角互补”是平行线的性质.
2.(2019 新抚区期末)如图,a∥b,a,b被直线c
所截,若∠1=140°,则∠2=( )
A.40° B.50°
C.60° D.70°
A
3.(2019 天心区校级期中)如图所示,AB∥CD ,
DB⊥BC于点B,若∠2=50°,则∠1=( )
A.40° B.50°
C.45° D.60°
A
a
b
c
1
2
A
B
C
D
1
2
4.如图,直线AB∥CD,BE平分∠ABC,交CD于
点D,∠CDB=30°,那么∠C的度数为 .
120°
5.如图,将一张长方形纸片ABCD沿BE折叠,若
∠CBA′ =40°,则∠BEA′ = .
65°
A
B
C
D
E
A'
A
B
C
D
E
由折叠的性质知,折叠后形成的图形全等,因此∠ABE=∠A′BE.再根据平行线的性质即可求得此题.
分析
6.如图,如果AB∥CD,那么 .(至少填三种)
B
1
4
3
2
6
5
F
E
D
C
A
8
7
从同位角的角度考虑
∠1=∠3、∠2=∠4、∠5=∠7、∠6=∠8.
从内错角的角度考虑
∠2=∠7、∠3=∠6.
从同旁内角的角度考虑
∠2+∠3=180°、∠6+∠7=180°.
B
C
A
D
解:∵ AB∥CD(已知),
∴ ∠B=∠C(两直线平行,内错角相等).
又∵ ∠B= 140 °(已知),
∴ ∠C=∠B= 140 °(等量代换).
7.一自行车运动员在一条公路上骑车,两次拐弯后,和原
来的方向相同(即拐弯前后的两条路互相平行),若测
得第一次拐弯的∠B是140°,则第二次拐弯的∠C应是
多少度才合理?为什么?
∴ ∠EFB=∠C=125°
(两直线平行,同位角相等).
8.如图,已知AB∥CD,∠C=125°,
∠A=45°,求∠E的度数.
解:∵ AB∥CD,∠C=125°(已知),
∵ ∠EFA =180°-∠EFB=180°-(∠A+∠E ),
∴ ∠EFB=∠A+∠E(等量代换).
由∵ ∠A=45°,
∴ ∠E=125°-45°=80°.
A
B
C
D
E
F
当堂检测 及时反馈
1.如图,一个含有30°角的直角三角
板的两个顶点分别放在一个长方形的对边上,如果
∠1=25°,那么∠2的度数是( )
A.100° B.105°
C.115° D.120°
C
2.如图,直线a∥b,若∠1是∠2
的2倍,则∠2的度数是( )
A.30° B.60°
C.90° D.120°
B
1
2
1
2
a
b
c
3.一副三角板按如下图放置,下列结论:①∠1=∠3;②若BC∥AD,则
∠4=∠3;③若∠2=15°必有∠4=2∠D;④若
∠2=30°,则有AC∥DE,其中正确的有( )
A.②④ B.①④
C.①②④ D.①③④
D
1
B
2
3
4
A
C
D
E
4.(2019 东西湖区期中)如图1,∠DEF=20°,将长方形纸
片ABCD沿直线EF折叠成图2,再沿折痕为BF折叠成图3,
则∠CFE的度数为( )
A.100° B.120° C.140° D.160°
B
A
E
D
A
E
A
E
D
C
F
B
C
B
C
F
B
G
D
F
G
图1
图2
图3
根据两直线平行,同旁内角互补可得∠CFE =180°-∠DEF,然后得出图2中∠CFE度数;再根据两直线平行,内错角相等可得∠BFE=∠DEF ,然后求出图2中∠BFC ,再根据翻折的性质可得∠CFE +∠BFE=∠BFC ,然后代入数据计算即可得解.
【分析】
5.把一块直尺与一块三角板如图
放置,若∠1=44°,则∠2的
度数是 .
134°
6.(2018·昆明禄劝期末)如图,∠1=∠2=∠3=50°。
则∠4 的度数是 .
130°
【易错提醒】利用平行线的性质和判定时,一定要清楚由角的关系推出平性关系是平行线的判定,由平行关系得到角的关系是平行线的性质.
4
3
1
2
1
4
3
2
①DE、BC平行吗?为什么?
②∠C等于多少度?为什么?
A
C
B
E
D
解:① DE∥BC.
∴ ∠C=∠AED(两直线平行,同位角相等).
∴ ∠ADE=∠B.
∴ DE∥BC(同位角相等,两直线平行).
② 由①得DE∥BC ,
又∵∠AED=80°(已知),
∴∠C=80°(等量代换).
7.如图,已知D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=80°.
∵ ∠ADE=60°,∠B=60°,
拓展提升 能力提升
1.如图所示,已知∠1=∠2,∠C=∠D, 试说明∠A=∠F.
∴ ∠4=∠C (两直线平行,同位角相等).
∵ ∠C=∠D (已知),
A
B
C
D
E
F
1
4
3
2
解:∵ ∠1=∠2 (已知),∠3=∠2(对顶角相等),
∴ ∠1=∠3 (等量代换).
∴ DB∥EC(同位角相等,两直线平行).
∴ ∠4=∠D(等量代换).
∴ DF∥AC(内错角相等,两直线平行).
∴ ∠A=∠F (两直线平行,内错角相等).
2.(2019 义安区期末)已知:如图,点C在∠AOB的一边OA上,
过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.
解:(1)∵ 直线DE∥OB,CF平分∠ACD,
∠O=40°,
∴ ∠ECF=∠ECA+∠ACF=40°+70°=110°;
∴ ∠ACE=40°,
∴ ∠ACD=140°,
∴ ∠ACF=70°,
∴ ∠ACE=∠O,∠ACF=∠FCD,
A
E
O
G
D
F
C
B
2.(2019 义安区期末)已知:如图,点C在∠AOB的一边OA上,
过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.
(2)证明:∵ CF平分∠ACD,CG⊥CF,
∠ACD+∠OCD=180°,
∴∠FCD+∠DCG=90°,∠ACF+∠OCG=90°,
∴∠DCG=∠OCG,
∴CG平分∠OCD.
∴∠ACF=∠FCD,∠FCG=90°,
A
E
O
G
D
F
C
B
总结反思 知识内化
图形
已知
结果
结论
同位角
内错角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
a
b
c
c
c
a//b
同位角相等.
两直线平行,
a//b
两直线平行,
内错角相等.
同旁内角互补.
a//b
两直线平行,
同旁内角
∠1=∠2
∠3=∠2
∠2=∠4=180°
∠2与∠4互补
平行线的性质
2.由 得到 的结论是 .
1.由 得到 的结论是 .
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
判定
请注意:
角的关系
两直线平行
用途:
证平行
两直线平行
角相等或互补
用途:
证角相等或互补
平行线的判定
平行线的性质
小结
性质
