6.3.1二项式定理 课件(共23张PPT)
文档属性
| 名称 | 6.3.1二项式定理 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 929.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 15:22:18 | ||
图片预览






文档简介
(共23张PPT)
6.3.1 二项式定理
学习目标:
1.能用计数原理和组合数证明二项式定理并了解相关概念及其特征.
(重点:掌握二项式定理和二项展开式的通项公式)
2.能解决与二项式定理有关的简单问题(会求二项式的展开式,二项展开式某一项)
难点:会求某一项的二项式系数与某一项的系数及区别)。
一.复习回顾,知根知底
1.初中学过的二项式还记得是什么?
比如:(a+b), (a+b) ,(a+b) , (a+b) ,(a+b) ..........等代数式,数学上我们统称为二项式,其一般形式为:(a+b) , (n∈N )
3.什么是组合及其组合数?
一般地,从n个不同元素中取出m(m≤n)个不同元素,没有顺序区别的合成一组,就叫作从n个不同元素中取出m个不同元素的一个组合。相应地,所有不同组合的个数,叫做从n个不同元素中取出m(m≤n)个不同元素的组合数。表示为C。
2.我们学过的计数原理有哪些?最重要的区别在于什么?
分类加法计数原理(每一类都可以完成)
分步乘法计数原理(每一步缺一不可)。
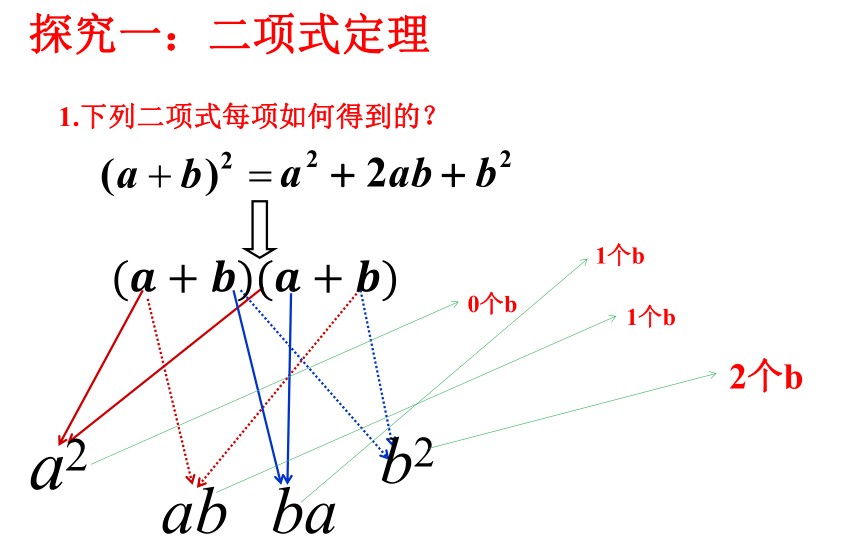
a2
ab
ba
b2
探究一:二项式定理
0个b
1个b
1个b
2个b
1.下列二项式每项如何得到的?
不要盲目运算,
要寻找展开式规律
探究一:二项式定理
二. 二项式定理
0个b
1个b
2个b
0个b
2个b
1个b
3个b
问题1:通过预习,观察规律,联系我们之前学过的计数原理,组合数。你能想到如何得到二项式展开式的每一项呢?
探究一:二项式定理
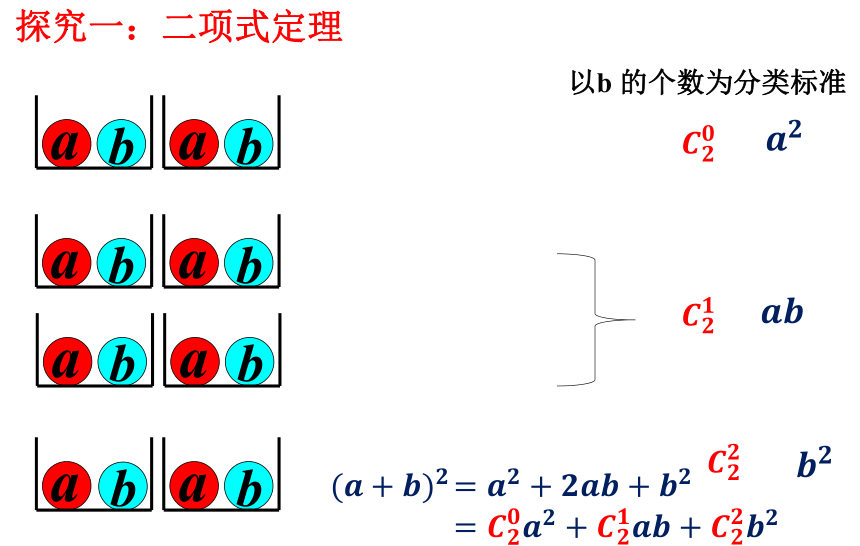
可以b 的个数为分类标准
探究一:二项式定理
以b 的个数为分类标准
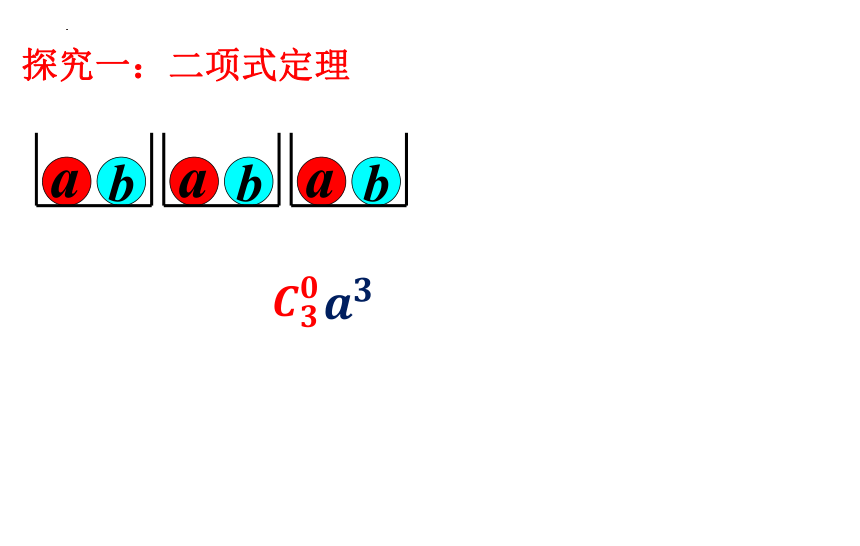
探究一:二项式定理
探究一:二项式定理
探究一:二项式定理
探究一:二项式定理
探究一:二项式定理
=
探究一:二项式定理
探究一:二项式定理
牛顿在1664-1665年间发现了二项式定理
二项式定理相关概念
3.二项展开式中,系数 叫作二项式系数, 即
2.二项展开式的通项:
1.
2.特征:
(1)项数:共有n+1项.
(3)字母按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
(2)次数:各项的次数都等于二项式的次数n;
的展开式
例1(1)
三.练习巩固,学会运用
例2:①求 (1+2x)7 的展开式的第4项;
②求 (1+2x)7 的展开式的第4项的系数;
③求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
系数与二项式系数区别
重难点应用:
重难点:二项式系数与项的系数的区别
1).注意对二项式定理的灵活应用.
2).注意区别二项式系数与项的系数的概念.
二项式系数:C
项的系数:二项式系数与数字系数的积
3).求二项式系数或项的系数的一种方法是将二项式展开.
变式 ①求 (1-2x)7 的展开式中第4项
②第4项的系数
③求 (1-2x)7 的展开式中第4项的二项式系数.
(2)-280
重难点应用:
四.作业布置:
1.教材课本31页练习题:1.2.4.
2.同步练习册学生版第25页题型一(1)(2)
3.题型二(1)
1.二项式定理:
2.通项:
3.二项式系数:C
第(k+1)项
注意:项的系数与二项式系数是两个不同的概念
五.课堂小结
6.3.1 二项式定理
学习目标:
1.能用计数原理和组合数证明二项式定理并了解相关概念及其特征.
(重点:掌握二项式定理和二项展开式的通项公式)
2.能解决与二项式定理有关的简单问题(会求二项式的展开式,二项展开式某一项)
难点:会求某一项的二项式系数与某一项的系数及区别)。
一.复习回顾,知根知底
1.初中学过的二项式还记得是什么?
比如:(a+b), (a+b) ,(a+b) , (a+b) ,(a+b) ..........等代数式,数学上我们统称为二项式,其一般形式为:(a+b) , (n∈N )
3.什么是组合及其组合数?
一般地,从n个不同元素中取出m(m≤n)个不同元素,没有顺序区别的合成一组,就叫作从n个不同元素中取出m个不同元素的一个组合。相应地,所有不同组合的个数,叫做从n个不同元素中取出m(m≤n)个不同元素的组合数。表示为C。
2.我们学过的计数原理有哪些?最重要的区别在于什么?
分类加法计数原理(每一类都可以完成)
分步乘法计数原理(每一步缺一不可)。
a2
ab
ba
b2
探究一:二项式定理
0个b
1个b
1个b
2个b
1.下列二项式每项如何得到的?
不要盲目运算,
要寻找展开式规律
探究一:二项式定理
二. 二项式定理
0个b
1个b
2个b
0个b
2个b
1个b
3个b
问题1:通过预习,观察规律,联系我们之前学过的计数原理,组合数。你能想到如何得到二项式展开式的每一项呢?
探究一:二项式定理
可以b 的个数为分类标准
探究一:二项式定理
以b 的个数为分类标准
探究一:二项式定理
探究一:二项式定理
探究一:二项式定理
探究一:二项式定理
探究一:二项式定理
=
探究一:二项式定理
探究一:二项式定理
牛顿在1664-1665年间发现了二项式定理
二项式定理相关概念
3.二项展开式中,系数 叫作二项式系数, 即
2.二项展开式的通项:
1.
2.特征:
(1)项数:共有n+1项.
(3)字母按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
(2)次数:各项的次数都等于二项式的次数n;
的展开式
例1(1)
三.练习巩固,学会运用
例2:①求 (1+2x)7 的展开式的第4项;
②求 (1+2x)7 的展开式的第4项的系数;
③求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
系数与二项式系数区别
重难点应用:
重难点:二项式系数与项的系数的区别
1).注意对二项式定理的灵活应用.
2).注意区别二项式系数与项的系数的概念.
二项式系数:C
项的系数:二项式系数与数字系数的积
3).求二项式系数或项的系数的一种方法是将二项式展开.
变式 ①求 (1-2x)7 的展开式中第4项
②第4项的系数
③求 (1-2x)7 的展开式中第4项的二项式系数.
(2)-280
重难点应用:
四.作业布置:
1.教材课本31页练习题:1.2.4.
2.同步练习册学生版第25页题型一(1)(2)
3.题型二(1)
1.二项式定理:
2.通项:
3.二项式系数:C
第(k+1)项
注意:项的系数与二项式系数是两个不同的概念
五.课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
