8.3解不等式组 课件(13张PPT)
文档属性
| 名称 | 8.3解不等式组 课件(13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 231.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
8.3
一元一次不等式组的解法
复习引入
1: 什么叫做一元一次不等式?
含有一个未知数,且含未知数的式子是整式,未知数的次数是1的不等式.
2: 解一元一次不等式的步骤有哪些?
(1)去分母 (2)去括号
(3)移项 (4)合并同类项
( 5) 系数化为1
小试身手
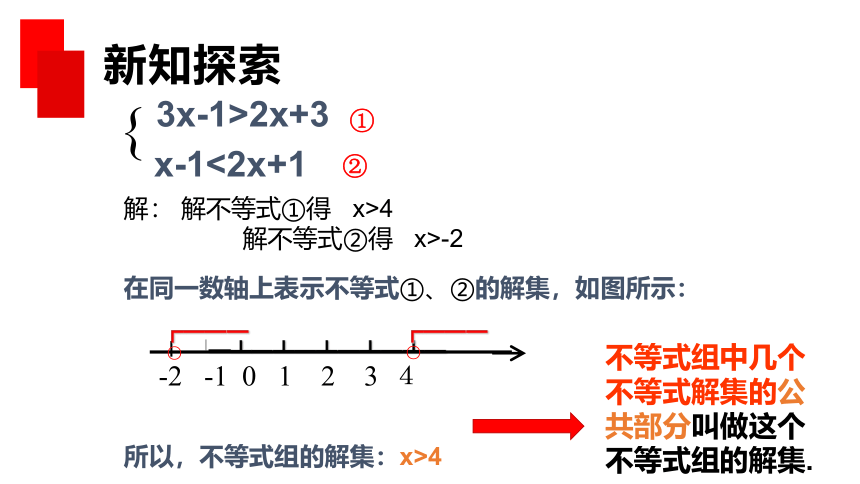
解不等式1: 3x-1>2x+3 2: x-1<2x+1
把以上两个不等式合在一起,就得到一个一元一次 不等式组
3x-1>2x+3
x-1<2x+1
{
新知探索
{
x-1<2x+1
3x-1>2x+3
①
②
解: 解不等式①得 x>4
解不等式②得 x>-2
在同一数轴上表示不等式①、②的解集,如图所示:
所以,不等式组的解集:x>4
━┻━┻━┻━┻━┻━
-2 -1 0 1 2 3 4
○
┏━━━
○
┏━━━
不等式组中几个不等式解集的公共部分叫做这个不等式组的解集.
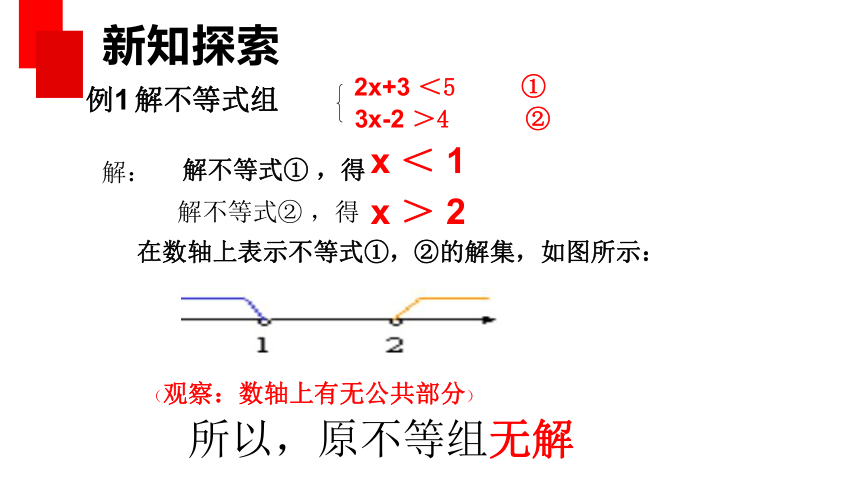
例1 解不等式组
2x+3 <5
3x-2 >4 ②
①
解:
解不等式① ,得
解不等式② ,得
x < 1
x > 2
在数轴上表示不等式①,②的解集,如图所示:
所以,原不等组无解
(观察:数轴上有无公共部分)
新知探索
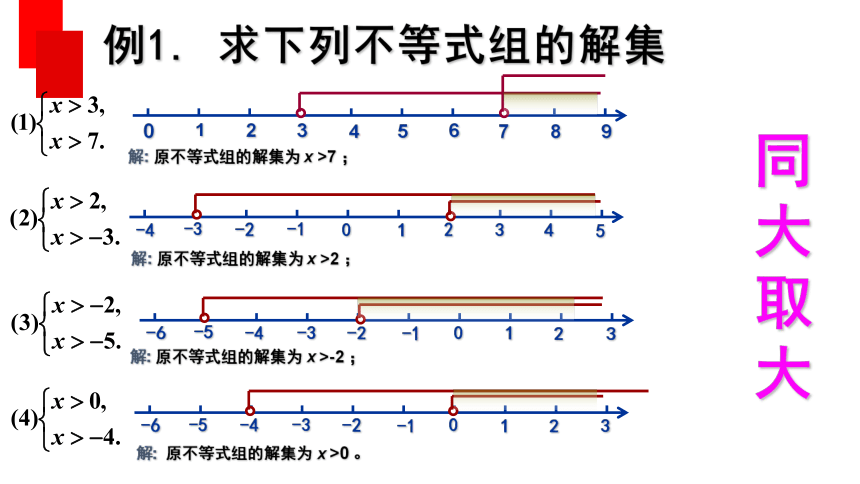
例1. 求下列不等式组的解集
:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 x >0 。
-6
1
0
-1
-2
-4
-5
-3
2
3
同大取大
. 求下列不等式组的解集
:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组的解集为 x ≤-4 。
-7
0
-1
-2
-3
-5
-6
-4
1
2
同小取小
. 求下列不等式组的解集
:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 -4大小,小大,中间找
. 求下列不等式组的解集
解: 原不等式组无解 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
大大,小小, 无解集
. 总结
一元一次不等式组的解集巧记
1 .皆大取大
2 .皆小取小
3 .介于其间,端点定好
4. 大大小小,无解
小试身手
x 2
x>3
{
x<2
x<3
{
x>2
x 3
{
x<2
x>3
{
④
①
②
③
(x>3)
(x<2)
(2(无解)
≥
≤
能力提升
5x < 0
3x-2 > 4
{
①
2x+3 ≥ -1
4x-2 < 2(x+3)
{
②
解下列不等式组
小结
解集:1在通过数轴确定不等式解集时,解集为几个不等式解集的公共部分
2不等式组的解集都能使组成该不等式组的每一个不等式成立,但是每个不等式的解集不一定能使其组成的不等式组成立。
3不等式的解集判定口诀:大大取最大、小小取最小、大小小大取中间、大大小小无解
8.3
一元一次不等式组的解法
复习引入
1: 什么叫做一元一次不等式?
含有一个未知数,且含未知数的式子是整式,未知数的次数是1的不等式.
2: 解一元一次不等式的步骤有哪些?
(1)去分母 (2)去括号
(3)移项 (4)合并同类项
( 5) 系数化为1
小试身手
解不等式1: 3x-1>2x+3 2: x-1<2x+1
把以上两个不等式合在一起,就得到一个一元一次 不等式组
3x-1>2x+3
x-1<2x+1
{
新知探索
{
x-1<2x+1
3x-1>2x+3
①
②
解: 解不等式①得 x>4
解不等式②得 x>-2
在同一数轴上表示不等式①、②的解集,如图所示:
所以,不等式组的解集:x>4
━┻━┻━┻━┻━┻━
-2 -1 0 1 2 3 4
○
┏━━━
○
┏━━━
不等式组中几个不等式解集的公共部分叫做这个不等式组的解集.
例1 解不等式组
2x+3 <5
3x-2 >4 ②
①
解:
解不等式① ,得
解不等式② ,得
x < 1
x > 2
在数轴上表示不等式①,②的解集,如图所示:
所以,原不等组无解
(观察:数轴上有无公共部分)
新知探索
例1. 求下列不等式组的解集
:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 x >0 。
-6
1
0
-1
-2
-4
-5
-3
2
3
同大取大
. 求下列不等式组的解集
:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组的解集为 x ≤-4 。
-7
0
-1
-2
-3
-5
-6
-4
1
2
同小取小
. 求下列不等式组的解集
:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组的解集为 -4
. 求下列不等式组的解集
解: 原不等式组无解 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解: 原不等式组无解 ;
解: 原不等式组无解 ;
解: 原不等式组无解 ;
大大,小小, 无解集
. 总结
一元一次不等式组的解集巧记
1 .皆大取大
2 .皆小取小
3 .介于其间,端点定好
4. 大大小小,无解
小试身手
x 2
x>3
{
x<2
x<3
{
x>2
x 3
{
x<2
x>3
{
④
①
②
③
(x>3)
(x<2)
(2
≥
≤
能力提升
5x < 0
3x-2 > 4
{
①
2x+3 ≥ -1
4x-2 < 2(x+3)
{
②
解下列不等式组
小结
解集:1在通过数轴确定不等式解集时,解集为几个不等式解集的公共部分
2不等式组的解集都能使组成该不等式组的每一个不等式成立,但是每个不等式的解集不一定能使其组成的不等式组成立。
3不等式的解集判定口诀:大大取最大、小小取最小、大小小大取中间、大大小小无解
