6.2.4+向量的数量积(2)(人教A版2019必修第二册课件)(共24张PPT)
文档属性
| 名称 | 6.2.4+向量的数量积(2)(人教A版2019必修第二册课件)(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-27 18:54:17 | ||
图片预览







文档简介
(共24张PPT)
学习目标
1.掌握平面向量数量积的运算律及常用的公式.
2.会利用向量数量积的有关运算律进行计算或证明.
核心素养:逻辑推理、直观想象、数学运算
一、温故知新:
1、数量积的定义:
其中:
特别地:
是向量
和
的夹角,范围是:
≤
≤
注意:
平面向量的数量积与向量的和、向量的差本质区别是什么?
平面向量的数量积是一个数量,而向量的和、向量的差分别是一个向量。
O
B
A
θ
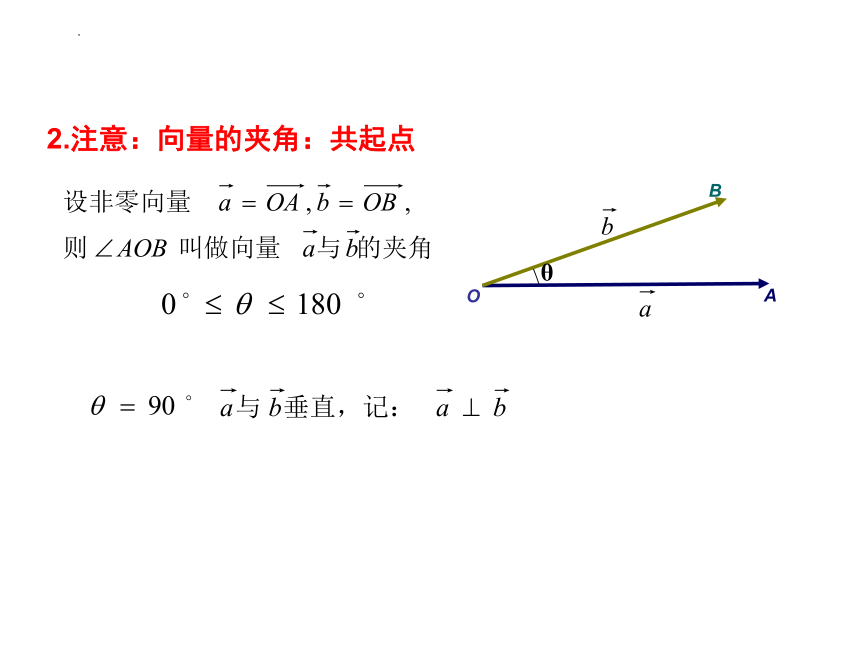
2.注意:向量的夹角:共起点
3、数量积的物理意义:
数量积的几何意义:
等于
的长度
与
在
的方向上的投影
的乘积。
θ
s
F
即
B1
4.投影向量的求法
(1)向量 a 在向量b 上的投影向量为|a |cos θ e (其中e
为与b同向的单位向量)
(2)向量 b 在向量a 上的投影向量为|b |cos θ e (其中e
为与a同向的单位向量)
5、数量积的主要性质:
(2)
(3)
与
同向
与
反向
特别地:
即
,
(4)
(5)
≤
(1)
6、平面向量数量积的运算律:
O
B
A
θ
O
B
A
θ
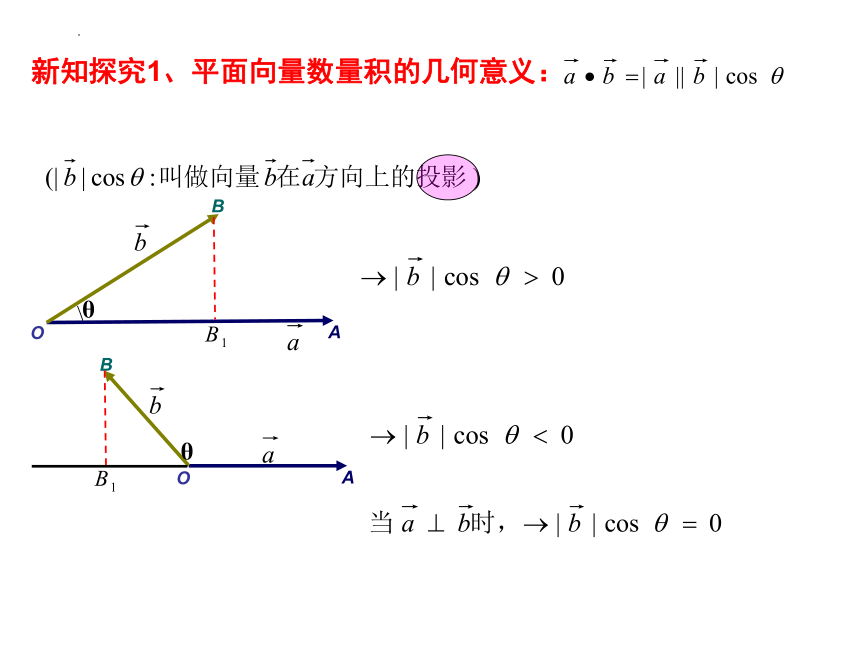
新知探究1、平面向量数量积的几何意义:
探究1、平面向量数量积的几何意义:
例1、已知e是单位向量,判断下列数量积的大小关系:
技巧:只需比较投影的大小
你学会了求数量积的两个技巧吗 (1)定义法(2)投影法
二、情境诱导,探求新知
利用向量线性运算可以解决平行、三点共线等问题,能解决垂直、角度、长度、距离等问题吗?
阅读课本17-21页,思考并完成以下问题
数量积运算中常用到哪些公式?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
例2. 我们知道,对任意a ,b∈R,恒有
对任意向量 是否也有下面类似的结论?
解:
因此,结论是成立的.
探究2:类比代数运算探究内积常用公式
常用公式
(1)(a+b)2=a2+2a·b+b2;
(2)(a-b)2=a2-2a·b+b2;
(3)(a+b)(a-b)=a2-b2;
(4)(a+b+c)2=a2+b2+c2+2a·b+2a·c+2b·c.
探究3:数量积、模的计算
解题技巧(求向量模的常见方法和思路)
(1)求模问题一般转化为求模的平方,与向量数量积联系要灵活应用a2=|a|2,勿忘记开方.
(2)a·a=a2=|a|2,此性质可用来求向量的模,可以实现实数运算与向量运算的相互转化.
探究4:垂直问题
探究5:夹角问题
深度探究:题设中,夹角改为锐角,如何求λ的范围
已 知 是非零向量,且 与
垂直,
与 垂直,
求 的夹角。
①
②
例6.
代入①得
解:
探究6:综合应用问题
例1.已知向量a,b的夹角为45°,且|a|=1,|2a-b|= ,则|b|=________.
解析:∵a,b的夹角为45°,|a|=1,
|2a-b|2=4-4×|b|+|b|2=10,
∴|b|=3.
∴a·b=|a||b|cos 45°=|b|,
备选例题
作业:练习T1-3+P23T12,P24T
作业:教材P2218-20,T24
1.“四基”清单:(1)向量数量积的运算律.
(2)利用数量积求向量的模和夹角. (3)向量垂直的应用.
2.方法归纳:类比法.
课堂小结
学习目标
1.掌握平面向量数量积的运算律及常用的公式.
2.会利用向量数量积的有关运算律进行计算或证明.
核心素养:逻辑推理、直观想象、数学运算
一、温故知新:
1、数量积的定义:
其中:
特别地:
是向量
和
的夹角,范围是:
≤
≤
注意:
平面向量的数量积与向量的和、向量的差本质区别是什么?
平面向量的数量积是一个数量,而向量的和、向量的差分别是一个向量。
O
B
A
θ
2.注意:向量的夹角:共起点
3、数量积的物理意义:
数量积的几何意义:
等于
的长度
与
在
的方向上的投影
的乘积。
θ
s
F
即
B1
4.投影向量的求法
(1)向量 a 在向量b 上的投影向量为|a |cos θ e (其中e
为与b同向的单位向量)
(2)向量 b 在向量a 上的投影向量为|b |cos θ e (其中e
为与a同向的单位向量)
5、数量积的主要性质:
(2)
(3)
与
同向
与
反向
特别地:
即
,
(4)
(5)
≤
(1)
6、平面向量数量积的运算律:
O
B
A
θ
O
B
A
θ
新知探究1、平面向量数量积的几何意义:
探究1、平面向量数量积的几何意义:
例1、已知e是单位向量,判断下列数量积的大小关系:
技巧:只需比较投影的大小
你学会了求数量积的两个技巧吗 (1)定义法(2)投影法
二、情境诱导,探求新知
利用向量线性运算可以解决平行、三点共线等问题,能解决垂直、角度、长度、距离等问题吗?
阅读课本17-21页,思考并完成以下问题
数量积运算中常用到哪些公式?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
例2. 我们知道,对任意a ,b∈R,恒有
对任意向量 是否也有下面类似的结论?
解:
因此,结论是成立的.
探究2:类比代数运算探究内积常用公式
常用公式
(1)(a+b)2=a2+2a·b+b2;
(2)(a-b)2=a2-2a·b+b2;
(3)(a+b)(a-b)=a2-b2;
(4)(a+b+c)2=a2+b2+c2+2a·b+2a·c+2b·c.
探究3:数量积、模的计算
解题技巧(求向量模的常见方法和思路)
(1)求模问题一般转化为求模的平方,与向量数量积联系要灵活应用a2=|a|2,勿忘记开方.
(2)a·a=a2=|a|2,此性质可用来求向量的模,可以实现实数运算与向量运算的相互转化.
探究4:垂直问题
探究5:夹角问题
深度探究:题设中,夹角改为锐角,如何求λ的范围
已 知 是非零向量,且 与
垂直,
与 垂直,
求 的夹角。
①
②
例6.
代入①得
解:
探究6:综合应用问题
例1.已知向量a,b的夹角为45°,且|a|=1,|2a-b|= ,则|b|=________.
解析:∵a,b的夹角为45°,|a|=1,
|2a-b|2=4-4×|b|+|b|2=10,
∴|b|=3.
∴a·b=|a||b|cos 45°=|b|,
备选例题
作业:练习T1-3+P23T12,P24T
作业:教材P2218-20,T24
1.“四基”清单:(1)向量数量积的运算律.
(2)利用数量积求向量的模和夹角. (3)向量垂直的应用.
2.方法归纳:类比法.
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
