【备考2023】浙教版科学中考核心考点训练(十):简单机械的计算【word,含解析】
文档属性
| 名称 | 【备考2023】浙教版科学中考核心考点训练(十):简单机械的计算【word,含解析】 |  | |
| 格式 | docx | ||
| 文件大小 | 162.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-03-28 12:51:35 | ||
图片预览



文档简介
简单机械的计算
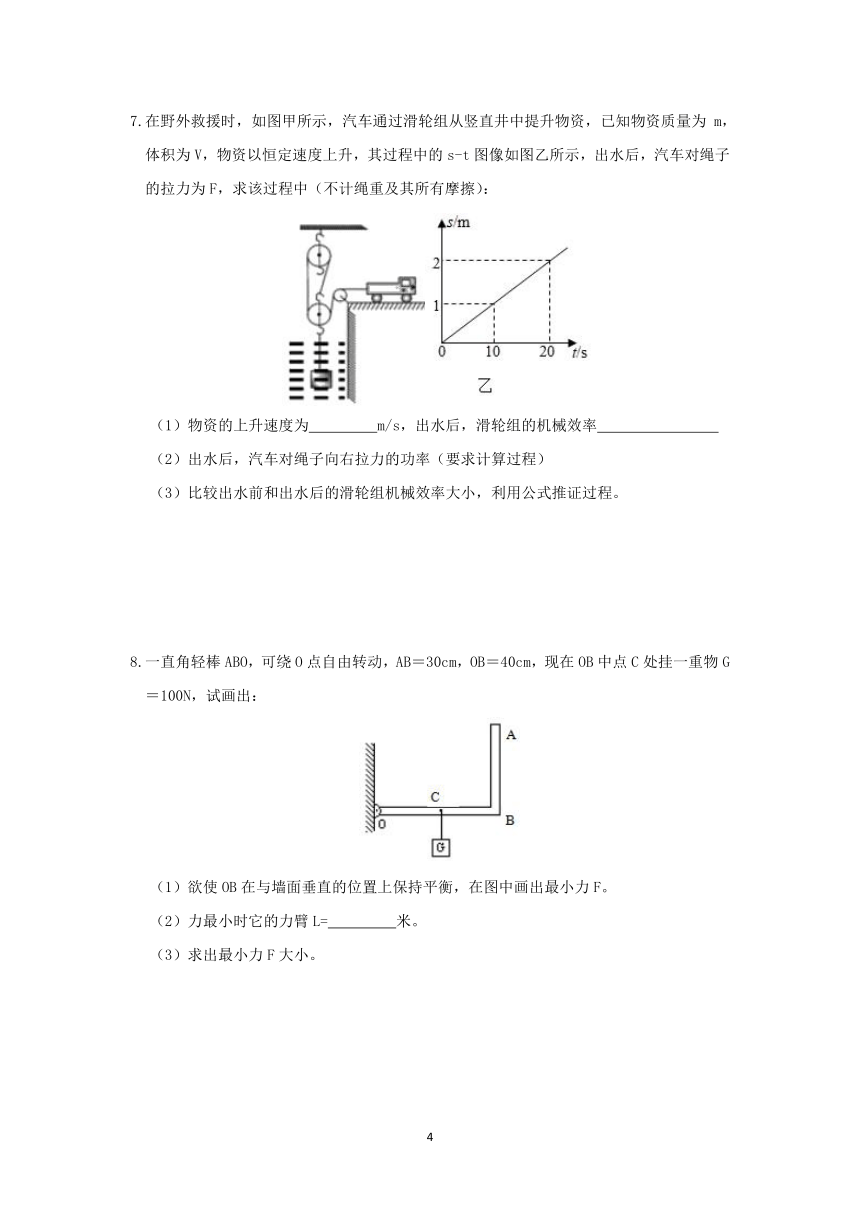
1.如图是搬运泥土的独轮车,设车箱和泥土的总重G=1800N,运泥土时从A点提起独轮车把手的力是F,问:
(1)独轮车属于 杠杆(选填“省力”或“费力”)。
(2)F的大小多少N?
(3)用同一辆车搬运相同的材料,若想更省力,手应向何处移动,请证明。
2.如图, 某工人用100的水平拉力F,抓紧绳子的一端,沿水平方向匀速向右运动10s内将矿井里重为160N的物体提升4m。若不计摩擦和绳重,求:
(1)动滑轮的重力;
(2)拉力F移动的速度为多少
3.小和尚甲、乙将总质量30kg的水桶(含水)用轻绳悬于轻质木棍的O点,分别在A、B点以竖直向上的力共同抬起木棍,如图,已知AO:BO=3:2,忽略手对木棍的作用力。
(1)将水桶从地面缓缓抬起50cm,至少需克服水桶(包括水)的重力做功多少 (g=10N/kg)
(2)若抬起水桶后木棍保持水平,小和尚乙肩部所受压力为多大?
4.如图静止在水平地面上一张左右对称的桌子,质量均匀分布。其大小为m,重心在O点(O点在整个桌子的中心),C点距地面高度CD=60cm,AD=80cm,BD=16cm,请回答:
(1)此时地面对桌子的支持力为
(2)若在小桌的C点用力F把桌腿B抬离地面,在图中画出最小的力F和重力臂并,求出最小力F大小。
5.如图,小型牵引机通过滑轮组匀速打捞起井中的物体。已知物体质量为120kg,密度为1.6×103kg/m3.物体在被拉出水面前后,牵引车作用在绳子上的拉力之比为1:2.不计摩擦、绳重及水的阻力。
(1)物体的体积多大?
(2)物体浸没在水中时所受的浮力是多少?
(3)物体出水面前,滑轮组的机械效率是多少?
6.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使 挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦不计)问:
(1)重为10N的钩码挂在A点时,拉力F为8N,钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m。问:人的拉力F与第一次相比 (选 填“变大”“变小”或“不变”)。
(3)比较此时的机械效率η2与η1的大小并用学过的知识给以推导。
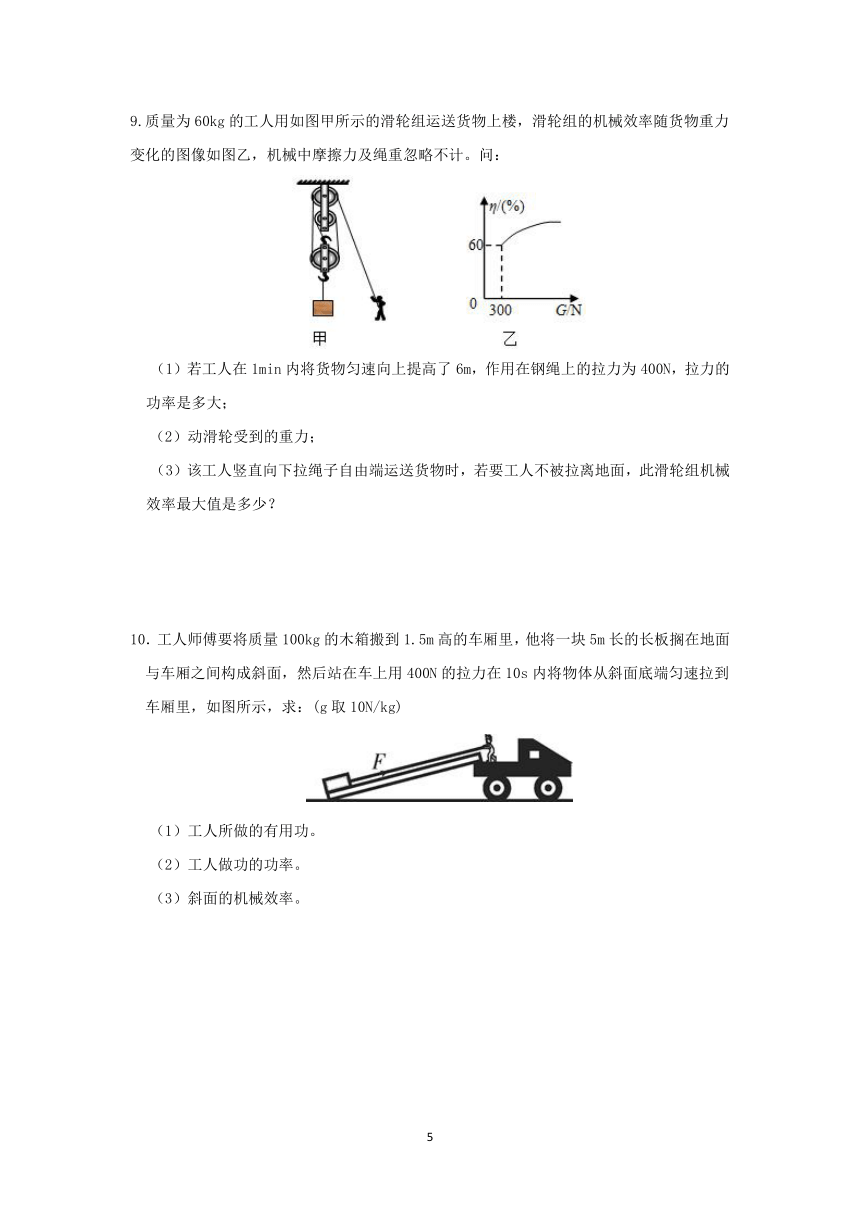
7.在野外救援时,如图甲所示,汽车通过滑轮组从竖直井中提升物资,已知物资质量为 m,体积为V,物资以恒定速度上升,其过程中的s-t图像如图乙所示,出水后,汽车对绳子的拉力为F,求该过程中(不计绳重及其所有摩擦):
(1)物资的上升速度为 m/s,出水后,滑轮组的机械效率
(2)出水后,汽车对绳子向右拉力的功率(要求计算过程)
(3)比较出水前和出水后的滑轮组机械效率大小,利用公式推证过程。
8.一直角轻棒ABO,可绕O点自由转动,AB=30cm,OB=40cm,现在OB中点C处挂一重物G=100N,试画出:
(1)欲使OB在与墙面垂直的位置上保持平衡,在图中画出最小力F。
(2)力最小时它的力臂L= 米。
(3)求出最小力F大小。
9.质量为60kg的工人用如图甲所示的滑轮组运送货物上楼,滑轮组的机械效率随货物重力变化的图像如图乙,机械中摩擦力及绳重忽略不计。问:
(1)若工人在1min内将货物匀速向上提高了6m,作用在钢绳上的拉力为400N,拉力的功率是多大;
(2)动滑轮受到的重力;
(3)该工人竖直向下拉绳子自由端运送货物时,若要工人不被拉离地面,此滑轮组机械效率最大值是多少?
10.工人师傅要将质量100kg的木箱搬到1.5m高的车厢里,他将一块5m长的长板搁在地面与车厢之间构成斜面,然后站在车上用400N的拉力在10s内将物体从斜面底端匀速拉到车厢里,如图所示,求:(g取10N/kg)
(1)工人所做的有用功。
(2)工人做功的功率。
(3)斜面的机械效率。
11.用图示装置探究“斜面机械效率”,实验记录如下表。
实验次数 物体种类 物重G/N 斜面高h/cm 沿斜面的拉力F/N 斜面长s/cm 机械效率η/%
1 木块 4 15 1.1 90 60.6
2 小车 4 15 90
(1)沿斜面拉动物体时,应使其做 运动。
(2)根据图中测力计的示数,可知第2次实验的机械效率为 %。由实验可得初步结论:斜面倾斜程度相同时, 越小,机械效率越大。
(3)第1次实验中,木块所受摩擦力为 N。
参考答案
1.(1)省力
(2)根据杠杆的平衡条件F1L1=F2L2得到:F×(0.4m+1.4m)=1800N×0.4m;
解得:F=400N。
(3)根据杠杆的平衡条件F1L1=F2L2得到:
动力 ;
在上面的式子中,F2和L2不变,则L1越大,F1越小;
因此手应该向右移动。
【解析】(1)比较动力臂和阻力臂的大小,从而确定杠杆的分类;
(2)根据杠杆的平衡条件F1L1=F2L2计算即可;
(3)当使用杠杆时,动力臂越长越省力,根据杠杆的平衡条件F1L1=F2L2分析解答。
2.(1)由图知,n=2,不计摩擦和绳重,
根据拉力可知,动滑轮重力:
G动=2F-G=2×100N-160N=40N;
(2)拉力端移动的距离s=2h=2×4m=8m,
拉力端移动的速度:。
3.(1)解:W=Gh=30kg×10N/kg×0.5m=150J
(2)解:以甲的肩膀为支点,动力为乙对杠杆的力F1,动力臂为l1为AB,阻力为绳子对杠杆的拉力F2=G水桶,阻力臂l2为OB,
由F1l1=F2l2得
F1= =300N× =120N,根据力的作用是相互的,小和尚乙肩膀所受的压力为120N。
4.(1)mg
(2)解:根据图片可知,在C点用力抬起桌腿,那么A点为支点,将AC为动力臂时最长,动力最小,如下图所示:
A点为杠杆的支点,桌子的重力G为阻力,阻力臂为:L2=;
动力臂L2=AC=;
根据杠杆的平衡条件F1L1=F2L2得到:mg×0.32m=F×1m;
解得:F=0.32mg。
【解析】(1)根据二力平衡的知识计算地面对桌子的支持力;
(2)当动力臂最长时动力最小,且以杠杆支点到力的作用点之间的线段为动力臂时最长。根据图片确定动力臂和阻力臂,根据杠杆的平衡条件F1L1=F2L2计算即可。
5.(1)由 可得,
物体的体积:;
(2)物体浸没在水中时所受的浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.075m3=750N;
(3)物体的重力:G=mg=120kg×10N/kg=1200N,
设物体在水中受到的拉力为F1,
因F1+F浮=G,
所以F1=G-F浮=1200N-750N=450N,
设出水面前、后牵引力作用在绳端的拉力为F、F′,动滑轮的重力为G1,
因不计摩擦、绳重及水的阻力
所以,物体出水面前:①
物体出水面后:②
由①②两式相比可得: ,
解得:G1=300N
根据①式得:,
物体出水面前的机械效率:。
6.(1)解:有用功:W有用=Gh=10N×0.3m=3J;
总功:W总=Fs=8N×0.5m=4J,
机械效率:η1= ×100%= ×100%=75%
(2)变小
(3)解:杠杆的机械效率:η= = = ;
从上面η的表达式可知:W有用减小、W额不变,所以 变大,分母变大,η就减小;
即:η2<η1
【解析】(1)根据 W有用=Gh 计算有用功,根据 W总=Fs 计算出总功,根据 计算机械效率;
(2)根据杠杆的平衡条件F1L1=F2L2分析解答;
(3)当拉力作用点向上移动的距离相同时,将钩码从A点移动到B点,根据相似三角形的特点可知,重物上升的高度h减小,根据W有=Gh可知,做的有用功减小。而杠杆上升的高度与原来相同,根据W额=G杠杆h可知,克服杠杆重力做的额外功相等,最后根据“ η= = = ”比较机械效率的变化即可。
7.(1)0.1; ×100%
(2)解:拉力移动的速度v'=nv=0.1m/s×3=0.3m/s;
拉力的功率:P=Fv'=F×0.3m/s=0.3F。
(3)解:出水之前,作用在动滑轮上的拉力等于物体的重力与浮力的差,
此时的机械效率为:;
出水后的机械效率为:;
比较可知,出水前η'小于出水后的η。
【解析】(1)根据乙图可知,物资上升的速度:;
出水后的机械效率:。
8.(1)解:由杠杆平衡条件F1 L1=F2 L2可知,在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小;图中支点在O点,因此OA作为动力臂最长,由图知动力的方向应该向上,如下图所示:
(2)0.5
(3)设在A点需加最小的力为F,并使F的方向垂直于OA,
由勾股定理可得,OA= = =50cm,
根据杠杆的平衡条件F OA=G OC,
得:F= =40N
9.(1)由图可知,承担重力的绳子段数n=3,
则绳端移动的距离:s=nh=3×6m=18m,
拉力做的功:W=Fs=400N×18m=7200J,
拉力的功率:;
答: 拉力的功率为120W。
(2)由图乙可知,物重G=300N时,滑轮组的机械效率η=60%,
则滑轮组的机械效率:;
即,
解得:G动=200N;
答:动滑轮受到的重力为200N
(3)已知工人的质量为60kg,
则该工人竖直向下拉绳子自由端运送货物时,绳子的最大拉力:
F大=G人=m人g=60kg×10N/kg=600N,
提升的最大物重:G大=nF大-G动=3×600N-200N=1600N,
则滑轮组的最大机械效率:。
答:滑轮组的机械效率最大值是88.9%。
【解析】(1)根据图片确定承担重力的绳子段数n,根据s=nh求出绳端移动的距离,根据W=Fs求出拉力做的功,利用 求出拉力的功率;
(2)由图乙可知,物重G=300N时,滑轮组的机械效率η=60%,根据求出动滑轮受到的重力;
(3)该工人竖直向下拉绳子自由端运送货物时,绳子的最大拉力等于人的重力,根据求出提升的最大物重,求出滑轮组的最大机械效率。
10.(1)解:木箱的重力G=mg=100kg×10N/kg=1000N,
工人师傅对木箱做的有用功W有用=Gh=1000N×1.5m=1500J。
(2)解:工人做的总功W总=Fs=400N×5m=2000J,
工人做功的功率P总= = =200W。
(3)解:斜面的机械效率η= ×100%= ×100%=75%。
11.(1)匀速直线(2)95.2(95也可以);摩擦力(3)0.43
【解析】(1)沿斜面拉动物体时,应使其做匀速直线运动。
(2)实验2中拉力为0.7N,那么它的机械效率为:;
根据公式F=f+FG可知,重力的分力FG不变,拉力越大,则摩擦力越大;因为实验2中的拉力小于实验1,且实验2的机械效率大,因此得到结论:斜面倾斜程度相同时,摩擦力越小,机械效率越大。
(3)第1次实验中:总功W总=Fs=1.1N×0.9m=0.99J;
有用功W有=Gh=4N×0.15m=0.6J;
额外功:W额=W总-W有=0.99J-0.6J=0.39J;
摩擦力为:。
(
1
)
1.如图是搬运泥土的独轮车,设车箱和泥土的总重G=1800N,运泥土时从A点提起独轮车把手的力是F,问:
(1)独轮车属于 杠杆(选填“省力”或“费力”)。
(2)F的大小多少N?
(3)用同一辆车搬运相同的材料,若想更省力,手应向何处移动,请证明。
2.如图, 某工人用100的水平拉力F,抓紧绳子的一端,沿水平方向匀速向右运动10s内将矿井里重为160N的物体提升4m。若不计摩擦和绳重,求:
(1)动滑轮的重力;
(2)拉力F移动的速度为多少
3.小和尚甲、乙将总质量30kg的水桶(含水)用轻绳悬于轻质木棍的O点,分别在A、B点以竖直向上的力共同抬起木棍,如图,已知AO:BO=3:2,忽略手对木棍的作用力。
(1)将水桶从地面缓缓抬起50cm,至少需克服水桶(包括水)的重力做功多少 (g=10N/kg)
(2)若抬起水桶后木棍保持水平,小和尚乙肩部所受压力为多大?
4.如图静止在水平地面上一张左右对称的桌子,质量均匀分布。其大小为m,重心在O点(O点在整个桌子的中心),C点距地面高度CD=60cm,AD=80cm,BD=16cm,请回答:
(1)此时地面对桌子的支持力为
(2)若在小桌的C点用力F把桌腿B抬离地面,在图中画出最小的力F和重力臂并,求出最小力F大小。
5.如图,小型牵引机通过滑轮组匀速打捞起井中的物体。已知物体质量为120kg,密度为1.6×103kg/m3.物体在被拉出水面前后,牵引车作用在绳子上的拉力之比为1:2.不计摩擦、绳重及水的阻力。
(1)物体的体积多大?
(2)物体浸没在水中时所受的浮力是多少?
(3)物体出水面前,滑轮组的机械效率是多少?
6.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使 挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦不计)问:
(1)重为10N的钩码挂在A点时,拉力F为8N,钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m。问:人的拉力F与第一次相比 (选 填“变大”“变小”或“不变”)。
(3)比较此时的机械效率η2与η1的大小并用学过的知识给以推导。
7.在野外救援时,如图甲所示,汽车通过滑轮组从竖直井中提升物资,已知物资质量为 m,体积为V,物资以恒定速度上升,其过程中的s-t图像如图乙所示,出水后,汽车对绳子的拉力为F,求该过程中(不计绳重及其所有摩擦):
(1)物资的上升速度为 m/s,出水后,滑轮组的机械效率
(2)出水后,汽车对绳子向右拉力的功率(要求计算过程)
(3)比较出水前和出水后的滑轮组机械效率大小,利用公式推证过程。
8.一直角轻棒ABO,可绕O点自由转动,AB=30cm,OB=40cm,现在OB中点C处挂一重物G=100N,试画出:
(1)欲使OB在与墙面垂直的位置上保持平衡,在图中画出最小力F。
(2)力最小时它的力臂L= 米。
(3)求出最小力F大小。
9.质量为60kg的工人用如图甲所示的滑轮组运送货物上楼,滑轮组的机械效率随货物重力变化的图像如图乙,机械中摩擦力及绳重忽略不计。问:
(1)若工人在1min内将货物匀速向上提高了6m,作用在钢绳上的拉力为400N,拉力的功率是多大;
(2)动滑轮受到的重力;
(3)该工人竖直向下拉绳子自由端运送货物时,若要工人不被拉离地面,此滑轮组机械效率最大值是多少?
10.工人师傅要将质量100kg的木箱搬到1.5m高的车厢里,他将一块5m长的长板搁在地面与车厢之间构成斜面,然后站在车上用400N的拉力在10s内将物体从斜面底端匀速拉到车厢里,如图所示,求:(g取10N/kg)
(1)工人所做的有用功。
(2)工人做功的功率。
(3)斜面的机械效率。
11.用图示装置探究“斜面机械效率”,实验记录如下表。
实验次数 物体种类 物重G/N 斜面高h/cm 沿斜面的拉力F/N 斜面长s/cm 机械效率η/%
1 木块 4 15 1.1 90 60.6
2 小车 4 15 90
(1)沿斜面拉动物体时,应使其做 运动。
(2)根据图中测力计的示数,可知第2次实验的机械效率为 %。由实验可得初步结论:斜面倾斜程度相同时, 越小,机械效率越大。
(3)第1次实验中,木块所受摩擦力为 N。
参考答案
1.(1)省力
(2)根据杠杆的平衡条件F1L1=F2L2得到:F×(0.4m+1.4m)=1800N×0.4m;
解得:F=400N。
(3)根据杠杆的平衡条件F1L1=F2L2得到:
动力 ;
在上面的式子中,F2和L2不变,则L1越大,F1越小;
因此手应该向右移动。
【解析】(1)比较动力臂和阻力臂的大小,从而确定杠杆的分类;
(2)根据杠杆的平衡条件F1L1=F2L2计算即可;
(3)当使用杠杆时,动力臂越长越省力,根据杠杆的平衡条件F1L1=F2L2分析解答。
2.(1)由图知,n=2,不计摩擦和绳重,
根据拉力可知,动滑轮重力:
G动=2F-G=2×100N-160N=40N;
(2)拉力端移动的距离s=2h=2×4m=8m,
拉力端移动的速度:。
3.(1)解:W=Gh=30kg×10N/kg×0.5m=150J
(2)解:以甲的肩膀为支点,动力为乙对杠杆的力F1,动力臂为l1为AB,阻力为绳子对杠杆的拉力F2=G水桶,阻力臂l2为OB,
由F1l1=F2l2得
F1= =300N× =120N,根据力的作用是相互的,小和尚乙肩膀所受的压力为120N。
4.(1)mg
(2)解:根据图片可知,在C点用力抬起桌腿,那么A点为支点,将AC为动力臂时最长,动力最小,如下图所示:
A点为杠杆的支点,桌子的重力G为阻力,阻力臂为:L2=;
动力臂L2=AC=;
根据杠杆的平衡条件F1L1=F2L2得到:mg×0.32m=F×1m;
解得:F=0.32mg。
【解析】(1)根据二力平衡的知识计算地面对桌子的支持力;
(2)当动力臂最长时动力最小,且以杠杆支点到力的作用点之间的线段为动力臂时最长。根据图片确定动力臂和阻力臂,根据杠杆的平衡条件F1L1=F2L2计算即可。
5.(1)由 可得,
物体的体积:;
(2)物体浸没在水中时所受的浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.075m3=750N;
(3)物体的重力:G=mg=120kg×10N/kg=1200N,
设物体在水中受到的拉力为F1,
因F1+F浮=G,
所以F1=G-F浮=1200N-750N=450N,
设出水面前、后牵引力作用在绳端的拉力为F、F′,动滑轮的重力为G1,
因不计摩擦、绳重及水的阻力
所以,物体出水面前:①
物体出水面后:②
由①②两式相比可得: ,
解得:G1=300N
根据①式得:,
物体出水面前的机械效率:。
6.(1)解:有用功:W有用=Gh=10N×0.3m=3J;
总功:W总=Fs=8N×0.5m=4J,
机械效率:η1= ×100%= ×100%=75%
(2)变小
(3)解:杠杆的机械效率:η= = = ;
从上面η的表达式可知:W有用减小、W额不变,所以 变大,分母变大,η就减小;
即:η2<η1
【解析】(1)根据 W有用=Gh 计算有用功,根据 W总=Fs 计算出总功,根据 计算机械效率;
(2)根据杠杆的平衡条件F1L1=F2L2分析解答;
(3)当拉力作用点向上移动的距离相同时,将钩码从A点移动到B点,根据相似三角形的特点可知,重物上升的高度h减小,根据W有=Gh可知,做的有用功减小。而杠杆上升的高度与原来相同,根据W额=G杠杆h可知,克服杠杆重力做的额外功相等,最后根据“ η= = = ”比较机械效率的变化即可。
7.(1)0.1; ×100%
(2)解:拉力移动的速度v'=nv=0.1m/s×3=0.3m/s;
拉力的功率:P=Fv'=F×0.3m/s=0.3F。
(3)解:出水之前,作用在动滑轮上的拉力等于物体的重力与浮力的差,
此时的机械效率为:;
出水后的机械效率为:;
比较可知,出水前η'小于出水后的η。
【解析】(1)根据乙图可知,物资上升的速度:;
出水后的机械效率:。
8.(1)解:由杠杆平衡条件F1 L1=F2 L2可知,在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小;图中支点在O点,因此OA作为动力臂最长,由图知动力的方向应该向上,如下图所示:
(2)0.5
(3)设在A点需加最小的力为F,并使F的方向垂直于OA,
由勾股定理可得,OA= = =50cm,
根据杠杆的平衡条件F OA=G OC,
得:F= =40N
9.(1)由图可知,承担重力的绳子段数n=3,
则绳端移动的距离:s=nh=3×6m=18m,
拉力做的功:W=Fs=400N×18m=7200J,
拉力的功率:;
答: 拉力的功率为120W。
(2)由图乙可知,物重G=300N时,滑轮组的机械效率η=60%,
则滑轮组的机械效率:;
即,
解得:G动=200N;
答:动滑轮受到的重力为200N
(3)已知工人的质量为60kg,
则该工人竖直向下拉绳子自由端运送货物时,绳子的最大拉力:
F大=G人=m人g=60kg×10N/kg=600N,
提升的最大物重:G大=nF大-G动=3×600N-200N=1600N,
则滑轮组的最大机械效率:。
答:滑轮组的机械效率最大值是88.9%。
【解析】(1)根据图片确定承担重力的绳子段数n,根据s=nh求出绳端移动的距离,根据W=Fs求出拉力做的功,利用 求出拉力的功率;
(2)由图乙可知,物重G=300N时,滑轮组的机械效率η=60%,根据求出动滑轮受到的重力;
(3)该工人竖直向下拉绳子自由端运送货物时,绳子的最大拉力等于人的重力,根据求出提升的最大物重,求出滑轮组的最大机械效率。
10.(1)解:木箱的重力G=mg=100kg×10N/kg=1000N,
工人师傅对木箱做的有用功W有用=Gh=1000N×1.5m=1500J。
(2)解:工人做的总功W总=Fs=400N×5m=2000J,
工人做功的功率P总= = =200W。
(3)解:斜面的机械效率η= ×100%= ×100%=75%。
11.(1)匀速直线(2)95.2(95也可以);摩擦力(3)0.43
【解析】(1)沿斜面拉动物体时,应使其做匀速直线运动。
(2)实验2中拉力为0.7N,那么它的机械效率为:;
根据公式F=f+FG可知,重力的分力FG不变,拉力越大,则摩擦力越大;因为实验2中的拉力小于实验1,且实验2的机械效率大,因此得到结论:斜面倾斜程度相同时,摩擦力越小,机械效率越大。
(3)第1次实验中:总功W总=Fs=1.1N×0.9m=0.99J;
有用功W有=Gh=4N×0.15m=0.6J;
额外功:W额=W总-W有=0.99J-0.6J=0.39J;
摩擦力为:。
(
1
)
同课章节目录
