九年级上数学第五章教案.doc[上学期]
文档属性
| 名称 | 九年级上数学第五章教案.doc[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 54.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-31 00:00:00 | ||
图片预览




文档简介
教 师 备 课 笔 记
上课日期 月 日 星期
课 题 5.1 反比例函数 课型 新授课
教学目标 1.从现实情境和已有知识经验出发,讨论两个变量之间的相依关系,加深对函数概念的理解。2.经历抽象反比例函数概念的进程,领会反比例函数的意义,理解反比例函数的概念。
教学重点 理解和领会反比例函数的概念。
教学难点 领悟反比例函数的概念。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
一.创设问题情境,引入新课 [师]我们在前面学过一次函数和正比例函数,知道一次函数的表达式为y=kx+b其中k,b为常数且k≠0,正比例函数的表达式为y=kx,其中k为不为零的常数,但是在现实生活中,并不是只有这两种类型的表达式,如从A地到B地的路程为1200 km,某人开车要从A地到月地,汽车的速度v(km/h)和时间t(h)之间的关系式为vt=1200,则t=中,t和v之间的关系式肯定不是正比例函数和一次函数的关系式,那么它们之间的关系式究竟是什么关系式呢 这就是本节课我们要揭开的奥秘. [师]我们今天要学习的是反比例函数,它是函数中的一种,首先我们先来回忆一下什么叫函数 1.复习函数的定义 [师]大家还记得函数的定义吗 在某变化过程中有两个变量x,y.若给定其中一个变量x的值,y都有唯一确定的值与它对应,则称y是x的函数.问题提出:电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)你能用含有R的代数式表示I吗?(2)利用写出的关系式完成下表:R/Ω20406080100I/A当R越来越大时,I怎样变化?当R越来越小呢?(3)变量I是R的函数吗?为什么?学生小组合作讨论。京沪高速公路全长约为1262 km,汽车沿京沪高速公路从上海驶往北京,汽车行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间有怎样的关系 变量t是v的函数吗 为什么 [师]经过刚才的例题讲解,大家可以独立完成此题.如有困难再进行交流. [生]由路程等于速度乘以时间可知1262=vt,则有t=.当给定一个v的值时,相应地就确定了一个t值,根据函数的定义可知t是v的函数. [师]从上面的两个例题得出关系式 I=和t=. 它们是函数吗 它们是正比例函数吗 是一次函数吗 [生]因为给定一个R的值,相应地就确定了一个I的值,所以I是R的函数;同理可知t是v的函数.但是从表达式来看,它们既不是正比例函数,也不是一次函数. [师]我们知道正比例函数的关系式为y=kx(k≠0),一次函数的关系式为y=kx+b(k,b为常数且k≠0).大家能否根据两个例题归纳出这一类函数的表达式呢 [生]可以.由I=与t=可知关系式为y= (k为常数且k≠0). 一般地,如果两个变量x、y之间的关系可以表示成y= (k为常数,k≠0)的形式,那么称y是x的反比例函数. 从y=中可知x作为分母,所以x不能为零.学生探究反比例函数变量的相依关系,领会其概念。二.、联系生活、丰富联想1.一个矩形的面积为20,相邻的两条边长分别为xcm和ycm。那么变量y是变量x的函数吗?为什么?学生先独立思考,再进行全班交流。2.某村有耕地346.2公顷,人数数量n逐年发生变化,那么该村人均占有耕地面积m(公顷/人)是全村人口数n的函数吗?为什么?学生先独立思考,再同桌交流,而后大组发言。3.y是x的反比例函数,下表给出了x与y的一些值:x-2-113…y2-1……(1)写出这个反比例函数的表达式;(2)根据函数表达式完成上表。学生先独立练习,而后再同桌交流,上讲台演示。三、随堂练习课本随堂练习 1、2四、课堂总结 本节课我们学习了反比例函数的定义,并归纳总结出反比例函数的表达式为y= (k为常数.k≠0),自变量x不能为零.还能根据定义和表达式判断某两个变最之间的关系是否是函数,是什么函数.五、布置作业 课本习题5.1 1、2
教 师 备 课 笔 记
上课日期 月 日 星期
课 题 5.2 反比例函数的图象与性质(一) 课型 新授课
教学目标 1.进一步熟悉作函数图象的主要步骤,会作反比例函数的图象。2.体会函数的三种表示方法的相互转换,对函数进行认识上的整合。3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质。
教学重点 掌握反比例函数的作图。
教学难点 反比例函数的三种表示方法的相互转换。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
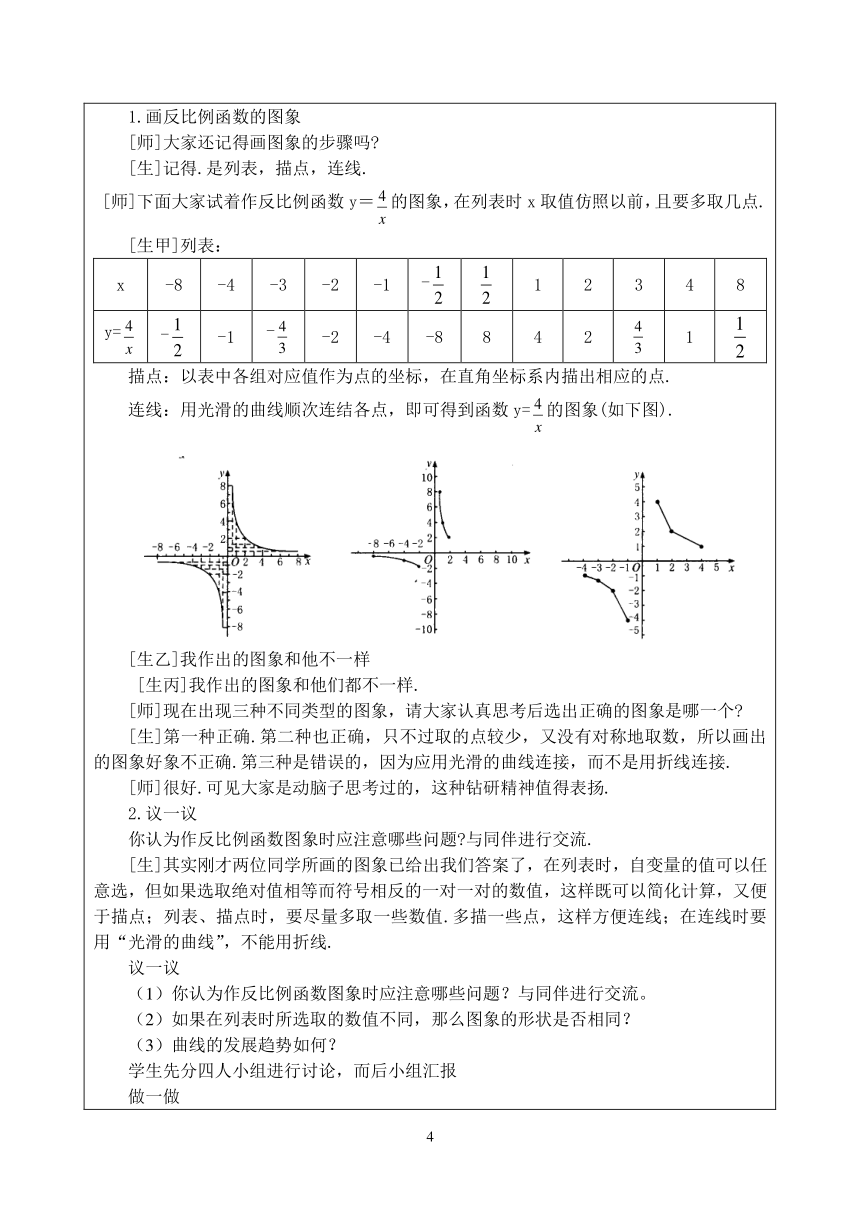
Ⅰ.创设问题情境,引入新课 [师]我们在前面学习了正比例函数和一次函数的图象,知道它们的图象都是一条直线,正比例函数的图象是过原点的一条直线,在画图象时需找(1,k)点即可,一次函数的图象也是一条直线,是不过原点的一条直线.画图象时只需找(0,b)和(-,0),过这两点作直线即可.那么反比例y= (k≠0)的图象是直线呢 还是曲线,这就需要我们动手去做一做,才能得出结论.本节课就让我们一齐来实践吧. Ⅱ.新课讲解 1.画反比例函数的图象 [师]大家还记得画图象的步骤吗 [生]记得.是列表,描点,连线. [师]下面大家试着作反比例函数y=的图象,在列表时x取值仿照以前,且要多取几点. [生甲]列表:x-8-4-3-2-1-12348y=--1--2-4-88421描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.连线:用光滑的曲线顺次连结各点,即可得到函数y=的图象(如下图). [生乙]我作出的图象和他不一样 [生丙]我作出的图象和他们都不一样. [师]现在出现三种不同类型的图象,请大家认真思考后选出正确的图象是哪一个 [生]第一种正确.第二种也正确,只不过取的点较少,又没有对称地取数,所以画出的图象好象不正确.第三种是错误的,因为应用光滑的曲线连接,而不是用折线连接. [师]很好.可见大家是动脑子思考过的,这种钻研精神值得表扬. 2.议一议 你认为作反比例函数图象时应注意哪些问题 与同伴进行交流. [生]其实刚才两位同学所画的图象已给出我们答案了,在列表时,自变量的值可以任意选,但如果选取绝对值相等而符号相反的一对一对的数值,这样既可以简化计算,又便于描点;列表、描点时,要尽量多取一些数值.多描一些点,这样方便连线;在连线时要用“光滑的曲线”,不能用折线.议一议(1)你认为作反比例函数图象时应注意哪些问题?与同伴进行交流。(2)如果在列表时所选取的数值不同,那么图象的形状是否相同?(3)曲线的发展趋势如何?学生先分四人小组进行讨论,而后小组汇报做一做作反比例函数的图象。 学生动手画图,相互观摩。想一想 : 观察和的图象,它们有什么相同点和不同点?学生小组讨论,弄清上述两个图象的异同点。 [生]相同点: (1)图象都是由两支曲线组成; (2)它们都不与坐标轴相交; (3)它们都不过原点; 不同点: 它们所在的象限不同.y=的两支曲线在第一和第三象限;y=的两支曲线在第二和第四象限. [师]很好,完全正确. 大家再仔细观察一下每个函数图象是否为对称图形. [生]是轴对称图形,也是中心对称图形. [师]由此看来,反比例函数的图象是两支双曲线,它们要么在第一、三象限,要么在第二、四象限,究竟什么时候在一、三象限,什么时候在二、四象限,大家能肯定吗 [生]可以,当k>0时,图象的两支曲线在第一、三象限内;当k<0时,两支曲线分别位于第二、四象限. [师]大家的观察能力和分析能力很了不起哟,继续努力.二、随堂练习课本随堂练习[探索与交流]对于函数来说,当x<0时,x的值逐渐减小,y的值将怎样变化?对于函数,当x>0时,x的值逐渐增大,y的值将怎样变化?学生分四人小组全班探索。三、课堂总结在进行函数的列表,描点作图的活动中,就已经渗透了反比例函数的性质,因此在作图象的过程中,大家要进行积极的探索。另外,反比例函数的图象是非线性的,它的图象是双曲线。四、布置作业 课本习题5.2 1
教 师 备 课 笔 记
上课日期 月 日 星期
课 题 5.2 反比例函数的图象与性质(二) 课型 新授课
教学目标 1.经历观察、归纳、交流的过程,逐步提高从函数图象中获取信息的能力,探索反比例函数的主要性质。2.提高学生的观察、分析能力和对图形的感知水平,使学生从整体上领会研究函数的一般要求。
教学重点 掌握反比例函数的主要性质。
教学难点 理解反比例函数的性质。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
一、观察联想、探究新知 [师]上节课我们学习了画反比例函数的图象,并通过图象总结出当k>0时,函数图象的两个分支分别位于第一、三象限内;当k<0时,函数图象的两个分支分别位于第二、四象限内.并讨论了反比例函数y=与y=-的图象的异同点.这是从函数的图象位于哪些象限来研究了反比例函数的. 我们知道在学习正比例函数和一次函数图象时,还研究了当k>0时,y的值随x的增大而增大,当k<0时,y的值随x值的增大而减小,即函数值随自变量的变化而变化的情况,以及函数图象与x轴,y轴的交点坐标.本节课我们来研究一下反比例函数的有关性质.观察反比例函数的图象,你能发现它们的共同特征吗?探索:(1)函数图象分别位于哪几个象限内? (2)在每一个象限内,随着x值的增大,y的值是怎样变化的?能说明这是为什么吗? (3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?为什么?学生观察,同桌交流,大胆发言,发表见解。二、自主探究、领悟规律议一议考察当k=-2,-4,-6时,反比例函数的图象,它们有哪些共同特征?学生通过相互交流、补充和修正。 [师]通过我们刚才的讨论,可以得出如下结论: 反比例函数y=的图象,当k>0时,在每一象限内,y的值随x值的增大而减小;当k<0时,在每一象限内,y的值随x值的增大而增大.想一想(1)在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为,和有什么关系?为什么? [生]设P(x1,y1),过P点分别作x轴,y轴的平行线,与两坐标轴围成的矩形面积为S1,则S1=|x1|·|y1|=|x1y1|.∵(x1,y1)在反比例函数y=图象上,所以y1=,即x1y1=k.∴S1=|k|. 同理可知S2=|k|, 所以S1=S2[师]从上面的图中可以看出,P、Q两点在同一支曲线上,如果P,Q分别在不同的曲线,情况又怎样呢 (2)将反比例函数的图象绕原点旋转180°后,能与原来的图象重合吗?学生分四人小组进行操作。三、随堂练习课本随堂练习 1、2四、课堂总结 1.反比例函数y=的图象,当k0时,在第一、三象限内,在每一象限内,y的值随,值的增大而减小;当k教 师 备 课 笔 记
上课日期 月 日 星期
课 题 5.3 反比例函数的应用 课型 新授课
教学目标 1.经历分析实际问题中变量之间的关系,建立反比例函数模型,进而解决问题的过程。2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力。
教学重点 掌握从实际问题中建构反比例函数模型。
教学难点 从实际问题中寻找变量之间的关系。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
一、回顾交流、情境导入蓄电池的电压为定值.使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如下图所示;(1)蓄电池的电压是多少 你能写出这一函数的表达式吗 (2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内 R/Ω345678910I/A4[师]从图形上来看,I和R之间可能是反比例函数关系.电压U就相当于反比例函数中的k.要写出函数的表达式,实际上就是确定k(U),只需要一个条件即可,而图中已给出了一个点的坐标,所以这个问题就解决了,填表实际上是已知自变量求函数值. [生]解:(1)由题意设函数表达式为I=∵A(9,4)在图象上,∴U=IR=36. ∴表达式为I=.蓄电池的电压是36伏.(2)表格中从左到右依次是:12,9,7.2,6,4.5,3.6. 电源不超过10 A,即I最大为10 A,代入关系式中得R=3.6,为最小电阻,所以用电器的可变电阻应控制在R≥3.6这个范围内.二、寓思与练、小组探究2.如图5-9,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为()探究:(1)请你分别写出这两个函数的表达式;(2)你能求出点B的坐标吗?你是怎样求的?与同伴交流。 [师]要求这两个函数的表达式,只要把A点的坐标代入即可求出k1,k2,求点B的坐标即求y=k1x与y=的交点. [生]解:(1)∵A(,2)既在y=k1x图象上,又在y=的图象上.∴k1=2,2=. ∴k1=2, k2=6∴表达式分别为y=2x,y=.y=2x,(2)由 得2x=, ∴x=±.y=当x=-时,y=-2.∴B(-,-2).3、某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务的情境。(1)请你解释他们这样做的道理。(2)当人和木板对湿地的压力一定时,随着木板面积S()的变化,人和木板对地面的压强P(Pa)将如何变化?(3)如果人和木板对湿地的压力合计600N,那么:①用含S的代数式表示P,P是S的反比例函数吗?为什么?②当木板面积为0.2时,压强是多少?③如果要求压强不超过6000Pa,木板面积至少要多大?④在直角坐标系中,作出相应的函数图象。⑤请利用图象对(2)和(3)作出直观解释,并与同伴交流。学生分四人小组进行探讨、交流。三、随堂练习1.某蓄水池的排水管每时排水8 m3,6 h可将满池水全部排空.(1)蓄水池的容积是多少 (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化 (3)写出t与Q之间的关系式;(4)如果准备在5 h内将满池水排空,那么每时的排水量至少为多少 (5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空 四、课堂总结本节课是用函数的观点处理实际问题,关键在于分析实际情境,建立函数模型,并进一步明确数学问题,将实际问题置于已有的知识背景之中,用数学知识重新解释这是什么?可以看什么?逐步形成考察实际问题的能力,在解决问题时,应充分利用函数的图象,渗透数形结合的思想。五、布置作业 课本习题5.4 1、2
教 师 备 课 笔 记
上课日期 月 日 星期
课题 回顾与思考 课型 新授
教学目标 1.经历抽象反比例函数概念的过程、领会反比例函数的意义,理解反比例函数的概念.2.会作反比例函数的图象,并探索和掌握反比例函数的主要性质.3.会从函数图象中获取信息,解决实际问题.
重点和难点 本章知识的网络结构.反比例函数的概念.会画反比例函数的图象,并掌握其性质.反比例函数的应用.
教具准备 投影片
师 生 活 动 过 程
Ⅰ.导入 [师]本章的内容已全部学完,请大家先回忆一下,本章学习了哪些主要内容 [生]反比例函数的定义;反比例函数的图象及性质;反比例函数的应用. Ⅱ.重点知识回顾 一、本章知识结构 [师]由刚才大家的回忆,我们一齐来构造本章内容结构图,好吗 1.本章内容框架 [师]同学们可以根据以上内容框架,用自己的语言归纳总结本章内容. 二、举出现实生活中有关反比例函数的实例,并归纳反比例函数概念. [生]例:当三角形的面积是12 cm2时,它的底边a(cm)是这个底边上的高h(cm)的函数. 解:a=. 在上式中,每给h一个值,相应地就确定了一个a的值.因此a是h的函数,又它们之间的关系符合y=(k≠0),因此,a是h的反比例函数. 三、说说函数y=和y=-的图象的联系和区别. [生]联系:(1)图象都是由两支曲线组成; (2)它们都不与坐标轴相交; (3)它们都不过原点,既是中心对称图形,又是轴对称图形. 区别:(1)它们所在的象限不同,y=的两支曲线在第一和第三象限;y=-的两支曲线在第二和第四象限. (2)y=的图象在每个象限内,y随x的增大而减小:y=-的图象在每个象限内,y随x的增大而增大. [师]还有一点.虽然y=和y=-的图象不同,但是在这两个函数图象上任取—点,过这两点分别作x轴、y轴的平行线,与坐标轴围成的矩形面积相等,都为2. 四、画反比例函数图象的步骤,讨论反比例函数图象的性质 [生]画图象的步骤有列表,描点,连线.在画反比例函数的图象时应注意:列表时自变量的取值应选取绝对值相等而符号相反的—对一对的数值,并尽量多取一些点,连线时要连成光滑的曲线,而不是折线.反比例函数图象的性质有: 1.反比例函数的图象是两支双曲线,当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限. 2.当k>0时.在每一个象限内,y随x的增大而减小;当k<0时,在每一个象限,y随x的增大而增大. 3.因为在y= (k≠0)中,x不能为0,y也不能为0,所以反比例函数的图象不可能与x轴相交,也不可能与y轴相交. 4. 在一个反比例函数图象上任取两点P,Q,过点P,Q分别作x、轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2则S1=S2 5. 反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴,对称中心是坐标原点. Ⅲ.课堂练习1.对于函数y=,当x>0时,y_______0,这部分图象在第______象限;对于y=-,当x<0时,y____0,这部分图象在第_____象限.2.函数y=的图象在第____象限内,在每一个象限内,y随x的增大而______.3.根据下列条件,分别确定函数y=的表达式(1)当x=2时,y=-3;(2)点(-)在双曲线y=上. Ⅳ.课时小结 本节课我们从现实世界出发,抽象出反比例函数的概念,比较了反比例函数y=和y=-的图象的联系和区别,归纳了反比例函数的图象和性质,并进一步进行了应用. Ⅴ.课后作业 复习题 A组
教后随笔
1、
PAGE
1
上课日期 月 日 星期
课 题 5.1 反比例函数 课型 新授课
教学目标 1.从现实情境和已有知识经验出发,讨论两个变量之间的相依关系,加深对函数概念的理解。2.经历抽象反比例函数概念的进程,领会反比例函数的意义,理解反比例函数的概念。
教学重点 理解和领会反比例函数的概念。
教学难点 领悟反比例函数的概念。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
一.创设问题情境,引入新课 [师]我们在前面学过一次函数和正比例函数,知道一次函数的表达式为y=kx+b其中k,b为常数且k≠0,正比例函数的表达式为y=kx,其中k为不为零的常数,但是在现实生活中,并不是只有这两种类型的表达式,如从A地到B地的路程为1200 km,某人开车要从A地到月地,汽车的速度v(km/h)和时间t(h)之间的关系式为vt=1200,则t=中,t和v之间的关系式肯定不是正比例函数和一次函数的关系式,那么它们之间的关系式究竟是什么关系式呢 这就是本节课我们要揭开的奥秘. [师]我们今天要学习的是反比例函数,它是函数中的一种,首先我们先来回忆一下什么叫函数 1.复习函数的定义 [师]大家还记得函数的定义吗 在某变化过程中有两个变量x,y.若给定其中一个变量x的值,y都有唯一确定的值与它对应,则称y是x的函数.问题提出:电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)你能用含有R的代数式表示I吗?(2)利用写出的关系式完成下表:R/Ω20406080100I/A当R越来越大时,I怎样变化?当R越来越小呢?(3)变量I是R的函数吗?为什么?学生小组合作讨论。京沪高速公路全长约为1262 km,汽车沿京沪高速公路从上海驶往北京,汽车行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间有怎样的关系 变量t是v的函数吗 为什么 [师]经过刚才的例题讲解,大家可以独立完成此题.如有困难再进行交流. [生]由路程等于速度乘以时间可知1262=vt,则有t=.当给定一个v的值时,相应地就确定了一个t值,根据函数的定义可知t是v的函数. [师]从上面的两个例题得出关系式 I=和t=. 它们是函数吗 它们是正比例函数吗 是一次函数吗 [生]因为给定一个R的值,相应地就确定了一个I的值,所以I是R的函数;同理可知t是v的函数.但是从表达式来看,它们既不是正比例函数,也不是一次函数. [师]我们知道正比例函数的关系式为y=kx(k≠0),一次函数的关系式为y=kx+b(k,b为常数且k≠0).大家能否根据两个例题归纳出这一类函数的表达式呢 [生]可以.由I=与t=可知关系式为y= (k为常数且k≠0). 一般地,如果两个变量x、y之间的关系可以表示成y= (k为常数,k≠0)的形式,那么称y是x的反比例函数. 从y=中可知x作为分母,所以x不能为零.学生探究反比例函数变量的相依关系,领会其概念。二.、联系生活、丰富联想1.一个矩形的面积为20,相邻的两条边长分别为xcm和ycm。那么变量y是变量x的函数吗?为什么?学生先独立思考,再进行全班交流。2.某村有耕地346.2公顷,人数数量n逐年发生变化,那么该村人均占有耕地面积m(公顷/人)是全村人口数n的函数吗?为什么?学生先独立思考,再同桌交流,而后大组发言。3.y是x的反比例函数,下表给出了x与y的一些值:x-2-113…y2-1……(1)写出这个反比例函数的表达式;(2)根据函数表达式完成上表。学生先独立练习,而后再同桌交流,上讲台演示。三、随堂练习课本随堂练习 1、2四、课堂总结 本节课我们学习了反比例函数的定义,并归纳总结出反比例函数的表达式为y= (k为常数.k≠0),自变量x不能为零.还能根据定义和表达式判断某两个变最之间的关系是否是函数,是什么函数.五、布置作业 课本习题5.1 1、2
教 师 备 课 笔 记
上课日期 月 日 星期
课 题 5.2 反比例函数的图象与性质(一) 课型 新授课
教学目标 1.进一步熟悉作函数图象的主要步骤,会作反比例函数的图象。2.体会函数的三种表示方法的相互转换,对函数进行认识上的整合。3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质。
教学重点 掌握反比例函数的作图。
教学难点 反比例函数的三种表示方法的相互转换。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
Ⅰ.创设问题情境,引入新课 [师]我们在前面学习了正比例函数和一次函数的图象,知道它们的图象都是一条直线,正比例函数的图象是过原点的一条直线,在画图象时需找(1,k)点即可,一次函数的图象也是一条直线,是不过原点的一条直线.画图象时只需找(0,b)和(-,0),过这两点作直线即可.那么反比例y= (k≠0)的图象是直线呢 还是曲线,这就需要我们动手去做一做,才能得出结论.本节课就让我们一齐来实践吧. Ⅱ.新课讲解 1.画反比例函数的图象 [师]大家还记得画图象的步骤吗 [生]记得.是列表,描点,连线. [师]下面大家试着作反比例函数y=的图象,在列表时x取值仿照以前,且要多取几点. [生甲]列表:x-8-4-3-2-1-12348y=--1--2-4-88421描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.连线:用光滑的曲线顺次连结各点,即可得到函数y=的图象(如下图). [生乙]我作出的图象和他不一样 [生丙]我作出的图象和他们都不一样. [师]现在出现三种不同类型的图象,请大家认真思考后选出正确的图象是哪一个 [生]第一种正确.第二种也正确,只不过取的点较少,又没有对称地取数,所以画出的图象好象不正确.第三种是错误的,因为应用光滑的曲线连接,而不是用折线连接. [师]很好.可见大家是动脑子思考过的,这种钻研精神值得表扬. 2.议一议 你认为作反比例函数图象时应注意哪些问题 与同伴进行交流. [生]其实刚才两位同学所画的图象已给出我们答案了,在列表时,自变量的值可以任意选,但如果选取绝对值相等而符号相反的一对一对的数值,这样既可以简化计算,又便于描点;列表、描点时,要尽量多取一些数值.多描一些点,这样方便连线;在连线时要用“光滑的曲线”,不能用折线.议一议(1)你认为作反比例函数图象时应注意哪些问题?与同伴进行交流。(2)如果在列表时所选取的数值不同,那么图象的形状是否相同?(3)曲线的发展趋势如何?学生先分四人小组进行讨论,而后小组汇报做一做作反比例函数的图象。 学生动手画图,相互观摩。想一想 : 观察和的图象,它们有什么相同点和不同点?学生小组讨论,弄清上述两个图象的异同点。 [生]相同点: (1)图象都是由两支曲线组成; (2)它们都不与坐标轴相交; (3)它们都不过原点; 不同点: 它们所在的象限不同.y=的两支曲线在第一和第三象限;y=的两支曲线在第二和第四象限. [师]很好,完全正确. 大家再仔细观察一下每个函数图象是否为对称图形. [生]是轴对称图形,也是中心对称图形. [师]由此看来,反比例函数的图象是两支双曲线,它们要么在第一、三象限,要么在第二、四象限,究竟什么时候在一、三象限,什么时候在二、四象限,大家能肯定吗 [生]可以,当k>0时,图象的两支曲线在第一、三象限内;当k<0时,两支曲线分别位于第二、四象限. [师]大家的观察能力和分析能力很了不起哟,继续努力.二、随堂练习课本随堂练习[探索与交流]对于函数来说,当x<0时,x的值逐渐减小,y的值将怎样变化?对于函数,当x>0时,x的值逐渐增大,y的值将怎样变化?学生分四人小组全班探索。三、课堂总结在进行函数的列表,描点作图的活动中,就已经渗透了反比例函数的性质,因此在作图象的过程中,大家要进行积极的探索。另外,反比例函数的图象是非线性的,它的图象是双曲线。四、布置作业 课本习题5.2 1
教 师 备 课 笔 记
上课日期 月 日 星期
课 题 5.2 反比例函数的图象与性质(二) 课型 新授课
教学目标 1.经历观察、归纳、交流的过程,逐步提高从函数图象中获取信息的能力,探索反比例函数的主要性质。2.提高学生的观察、分析能力和对图形的感知水平,使学生从整体上领会研究函数的一般要求。
教学重点 掌握反比例函数的主要性质。
教学难点 理解反比例函数的性质。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
一、观察联想、探究新知 [师]上节课我们学习了画反比例函数的图象,并通过图象总结出当k>0时,函数图象的两个分支分别位于第一、三象限内;当k<0时,函数图象的两个分支分别位于第二、四象限内.并讨论了反比例函数y=与y=-的图象的异同点.这是从函数的图象位于哪些象限来研究了反比例函数的. 我们知道在学习正比例函数和一次函数图象时,还研究了当k>0时,y的值随x的增大而增大,当k<0时,y的值随x值的增大而减小,即函数值随自变量的变化而变化的情况,以及函数图象与x轴,y轴的交点坐标.本节课我们来研究一下反比例函数的有关性质.观察反比例函数的图象,你能发现它们的共同特征吗?探索:(1)函数图象分别位于哪几个象限内? (2)在每一个象限内,随着x值的增大,y的值是怎样变化的?能说明这是为什么吗? (3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?为什么?学生观察,同桌交流,大胆发言,发表见解。二、自主探究、领悟规律议一议考察当k=-2,-4,-6时,反比例函数的图象,它们有哪些共同特征?学生通过相互交流、补充和修正。 [师]通过我们刚才的讨论,可以得出如下结论: 反比例函数y=的图象,当k>0时,在每一象限内,y的值随x值的增大而减小;当k<0时,在每一象限内,y的值随x值的增大而增大.想一想(1)在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为,和有什么关系?为什么? [生]设P(x1,y1),过P点分别作x轴,y轴的平行线,与两坐标轴围成的矩形面积为S1,则S1=|x1|·|y1|=|x1y1|.∵(x1,y1)在反比例函数y=图象上,所以y1=,即x1y1=k.∴S1=|k|. 同理可知S2=|k|, 所以S1=S2[师]从上面的图中可以看出,P、Q两点在同一支曲线上,如果P,Q分别在不同的曲线,情况又怎样呢 (2)将反比例函数的图象绕原点旋转180°后,能与原来的图象重合吗?学生分四人小组进行操作。三、随堂练习课本随堂练习 1、2四、课堂总结 1.反比例函数y=的图象,当k0时,在第一、三象限内,在每一象限内,y的值随,值的增大而减小;当k
上课日期 月 日 星期
课 题 5.3 反比例函数的应用 课型 新授课
教学目标 1.经历分析实际问题中变量之间的关系,建立反比例函数模型,进而解决问题的过程。2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力。
教学重点 掌握从实际问题中建构反比例函数模型。
教学难点 从实际问题中寻找变量之间的关系。
教学方法 自主探究法
教学后记
教 学 内 容 及 过 程
一、回顾交流、情境导入蓄电池的电压为定值.使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如下图所示;(1)蓄电池的电压是多少 你能写出这一函数的表达式吗 (2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内 R/Ω345678910I/A4[师]从图形上来看,I和R之间可能是反比例函数关系.电压U就相当于反比例函数中的k.要写出函数的表达式,实际上就是确定k(U),只需要一个条件即可,而图中已给出了一个点的坐标,所以这个问题就解决了,填表实际上是已知自变量求函数值. [生]解:(1)由题意设函数表达式为I=∵A(9,4)在图象上,∴U=IR=36. ∴表达式为I=.蓄电池的电压是36伏.(2)表格中从左到右依次是:12,9,7.2,6,4.5,3.6. 电源不超过10 A,即I最大为10 A,代入关系式中得R=3.6,为最小电阻,所以用电器的可变电阻应控制在R≥3.6这个范围内.二、寓思与练、小组探究2.如图5-9,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为()探究:(1)请你分别写出这两个函数的表达式;(2)你能求出点B的坐标吗?你是怎样求的?与同伴交流。 [师]要求这两个函数的表达式,只要把A点的坐标代入即可求出k1,k2,求点B的坐标即求y=k1x与y=的交点. [生]解:(1)∵A(,2)既在y=k1x图象上,又在y=的图象上.∴k1=2,2=. ∴k1=2, k2=6∴表达式分别为y=2x,y=.y=2x,(2)由 得2x=, ∴x=±.y=当x=-时,y=-2.∴B(-,-2).3、某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,构筑成一条临时通道,从而顺利完成了任务的情境。(1)请你解释他们这样做的道理。(2)当人和木板对湿地的压力一定时,随着木板面积S()的变化,人和木板对地面的压强P(Pa)将如何变化?(3)如果人和木板对湿地的压力合计600N,那么:①用含S的代数式表示P,P是S的反比例函数吗?为什么?②当木板面积为0.2时,压强是多少?③如果要求压强不超过6000Pa,木板面积至少要多大?④在直角坐标系中,作出相应的函数图象。⑤请利用图象对(2)和(3)作出直观解释,并与同伴交流。学生分四人小组进行探讨、交流。三、随堂练习1.某蓄水池的排水管每时排水8 m3,6 h可将满池水全部排空.(1)蓄水池的容积是多少 (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化 (3)写出t与Q之间的关系式;(4)如果准备在5 h内将满池水排空,那么每时的排水量至少为多少 (5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空 四、课堂总结本节课是用函数的观点处理实际问题,关键在于分析实际情境,建立函数模型,并进一步明确数学问题,将实际问题置于已有的知识背景之中,用数学知识重新解释这是什么?可以看什么?逐步形成考察实际问题的能力,在解决问题时,应充分利用函数的图象,渗透数形结合的思想。五、布置作业 课本习题5.4 1、2
教 师 备 课 笔 记
上课日期 月 日 星期
课题 回顾与思考 课型 新授
教学目标 1.经历抽象反比例函数概念的过程、领会反比例函数的意义,理解反比例函数的概念.2.会作反比例函数的图象,并探索和掌握反比例函数的主要性质.3.会从函数图象中获取信息,解决实际问题.
重点和难点 本章知识的网络结构.反比例函数的概念.会画反比例函数的图象,并掌握其性质.反比例函数的应用.
教具准备 投影片
师 生 活 动 过 程
Ⅰ.导入 [师]本章的内容已全部学完,请大家先回忆一下,本章学习了哪些主要内容 [生]反比例函数的定义;反比例函数的图象及性质;反比例函数的应用. Ⅱ.重点知识回顾 一、本章知识结构 [师]由刚才大家的回忆,我们一齐来构造本章内容结构图,好吗 1.本章内容框架 [师]同学们可以根据以上内容框架,用自己的语言归纳总结本章内容. 二、举出现实生活中有关反比例函数的实例,并归纳反比例函数概念. [生]例:当三角形的面积是12 cm2时,它的底边a(cm)是这个底边上的高h(cm)的函数. 解:a=. 在上式中,每给h一个值,相应地就确定了一个a的值.因此a是h的函数,又它们之间的关系符合y=(k≠0),因此,a是h的反比例函数. 三、说说函数y=和y=-的图象的联系和区别. [生]联系:(1)图象都是由两支曲线组成; (2)它们都不与坐标轴相交; (3)它们都不过原点,既是中心对称图形,又是轴对称图形. 区别:(1)它们所在的象限不同,y=的两支曲线在第一和第三象限;y=-的两支曲线在第二和第四象限. (2)y=的图象在每个象限内,y随x的增大而减小:y=-的图象在每个象限内,y随x的增大而增大. [师]还有一点.虽然y=和y=-的图象不同,但是在这两个函数图象上任取—点,过这两点分别作x轴、y轴的平行线,与坐标轴围成的矩形面积相等,都为2. 四、画反比例函数图象的步骤,讨论反比例函数图象的性质 [生]画图象的步骤有列表,描点,连线.在画反比例函数的图象时应注意:列表时自变量的取值应选取绝对值相等而符号相反的—对一对的数值,并尽量多取一些点,连线时要连成光滑的曲线,而不是折线.反比例函数图象的性质有: 1.反比例函数的图象是两支双曲线,当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限. 2.当k>0时.在每一个象限内,y随x的增大而减小;当k<0时,在每一个象限,y随x的增大而增大. 3.因为在y= (k≠0)中,x不能为0,y也不能为0,所以反比例函数的图象不可能与x轴相交,也不可能与y轴相交. 4. 在一个反比例函数图象上任取两点P,Q,过点P,Q分别作x、轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2则S1=S2 5. 反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴,对称中心是坐标原点. Ⅲ.课堂练习1.对于函数y=,当x>0时,y_______0,这部分图象在第______象限;对于y=-,当x<0时,y____0,这部分图象在第_____象限.2.函数y=的图象在第____象限内,在每一个象限内,y随x的增大而______.3.根据下列条件,分别确定函数y=的表达式(1)当x=2时,y=-3;(2)点(-)在双曲线y=上. Ⅳ.课时小结 本节课我们从现实世界出发,抽象出反比例函数的概念,比较了反比例函数y=和y=-的图象的联系和区别,归纳了反比例函数的图象和性质,并进一步进行了应用. Ⅴ.课后作业 复习题 A组
教后随笔
1、
PAGE
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
