人教版四年级下册数学《三角形边的关系》课件(共22张PPT)
文档属性
| 名称 | 人教版四年级下册数学《三角形边的关系》课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 06:11:15 | ||
图片预览







文档简介
(共22张PPT)
三角形边的关系
5 三角形
学习目标
1.结合具体的情境让学生亲自动手操作,探索并发现三角形任意两边的和
大于第三条边。引导学生判断指定长度的三条线段能否组成三角形。
2.培养学生初步应用数学知识解决实际问题的能力,在探索与发现中感受
数学与日常生活的密切联系。
学习重难点
通过探索充分理解三角形任意两边之和大于第三边。
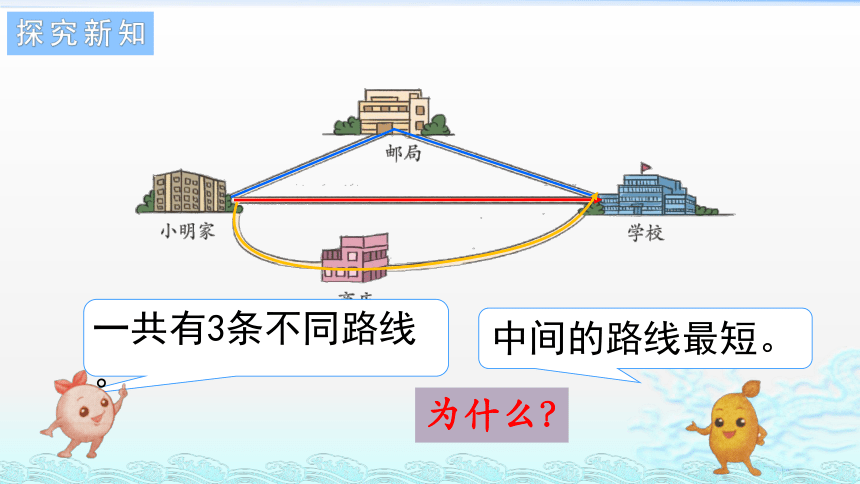
小明从家到学校的路线有几条?走哪条路线最近?
探究新知
一共有3条不同路线。
中间的路线最短。
为什么?
探究新知
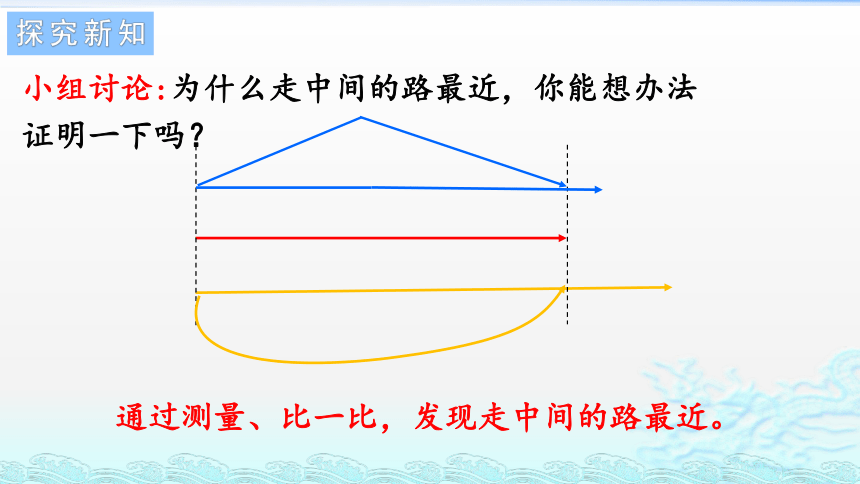
小组讨论:为什么走中间的路最近,你能想办法
证明一下吗?
通过测量、比一比,发现走中间的路最近。
探究新知
思考:通过小组探讨,你们得出了什么结论?
结
论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
课堂小结
我们来做个实验。
剪出下面4组纸条(单位:cm)。
(1)6、7、8。
(2)4、5、9。
(3)3、6、10。
(4)8、11、11。
用每组纸条摆三角形。
每组纸条都能摆出三角形吗?试一试!
探究新知
我摆成了一个三角形。
我怎么摆不成呢?
尝试摆一摆你发现了什么?
探究新知
4
5
9
6
7
8
(1)
(2)
3
6
10
8
11
11
(3)
(4)
探究新知
4
5
9
(1)
(2)
6
7
8
√
3
6
10
8
11
11
(3)
(4)
探究新知
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
探究新知
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
×
探究新知
(1)
(2)
6
7
8
√
×
(3)
(4)
8
11
11
×
√
4
5
9
3
6
10
观察下面的数据,你有什么发现?
探究新知
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
探究新知
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
探究新知
结
论
三角形任意两边的和大于第三边。
课堂小结
√
思
考
三角形任意两边的差与第三边的
关系?
(1)两点间线段长度小于曲线长度。
(2)三角形中两边的和大于第三边。
用今天学过的知识说一说为什么中间的路线最短。
√
巩固练习
( )
( )
在能拼成三角形的各组小棒下面画“√”。
√
√
(1)
(3)
(2)
(4)
( )
( )
巩固练习
一个三角形两条边是5厘米和10厘米,第三条边的长度(整厘米数)最短是多少厘米?最长是多少厘米?
三角形中,任意两边之和大于第三边,较短两边之和一定大于最长的边。
①第三条最短为:10-5+1=6(厘米)
②第三条最长为:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
巩固练习
1、如果一个三角形三条边长都是整厘米数,其中两条边分别长8cm和14cm,
则第三条边最长是( ),最短是( )。
2、如果一个三角形的两条边分别是30cm和40cm,那么第三条边可能是( )。
A. 80 B. 70
C. 60 D. 90
c
21cm
7cm
知识汇总
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
2. 三角形三边的关系:三角形任意两边的和大于第三边;三角形任意两边之差小于第三边。
3.判断三条线段能否围成三角形,只要把最短的两条边相加与最长边比较即可,如果最短的两边之和大于第三边,三条线段就能围成三角形。
感谢观看
四年级
三角形边的关系
5 三角形
学习目标
1.结合具体的情境让学生亲自动手操作,探索并发现三角形任意两边的和
大于第三条边。引导学生判断指定长度的三条线段能否组成三角形。
2.培养学生初步应用数学知识解决实际问题的能力,在探索与发现中感受
数学与日常生活的密切联系。
学习重难点
通过探索充分理解三角形任意两边之和大于第三边。
小明从家到学校的路线有几条?走哪条路线最近?
探究新知
一共有3条不同路线。
中间的路线最短。
为什么?
探究新知
小组讨论:为什么走中间的路最近,你能想办法
证明一下吗?
通过测量、比一比,发现走中间的路最近。
探究新知
思考:通过小组探讨,你们得出了什么结论?
结
论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
课堂小结
我们来做个实验。
剪出下面4组纸条(单位:cm)。
(1)6、7、8。
(2)4、5、9。
(3)3、6、10。
(4)8、11、11。
用每组纸条摆三角形。
每组纸条都能摆出三角形吗?试一试!
探究新知
我摆成了一个三角形。
我怎么摆不成呢?
尝试摆一摆你发现了什么?
探究新知
4
5
9
6
7
8
(1)
(2)
3
6
10
8
11
11
(3)
(4)
探究新知
4
5
9
(1)
(2)
6
7
8
√
3
6
10
8
11
11
(3)
(4)
探究新知
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
探究新知
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
×
探究新知
(1)
(2)
6
7
8
√
×
(3)
(4)
8
11
11
×
√
4
5
9
3
6
10
观察下面的数据,你有什么发现?
探究新知
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
探究新知
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
探究新知
结
论
三角形任意两边的和大于第三边。
课堂小结
√
思
考
三角形任意两边的差与第三边的
关系?
(1)两点间线段长度小于曲线长度。
(2)三角形中两边的和大于第三边。
用今天学过的知识说一说为什么中间的路线最短。
√
巩固练习
( )
( )
在能拼成三角形的各组小棒下面画“√”。
√
√
(1)
(3)
(2)
(4)
( )
( )
巩固练习
一个三角形两条边是5厘米和10厘米,第三条边的长度(整厘米数)最短是多少厘米?最长是多少厘米?
三角形中,任意两边之和大于第三边,较短两边之和一定大于最长的边。
①第三条最短为:10-5+1=6(厘米)
②第三条最长为:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
巩固练习
1、如果一个三角形三条边长都是整厘米数,其中两条边分别长8cm和14cm,
则第三条边最长是( ),最短是( )。
2、如果一个三角形的两条边分别是30cm和40cm,那么第三条边可能是( )。
A. 80 B. 70
C. 60 D. 90
c
21cm
7cm
知识汇总
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
2. 三角形三边的关系:三角形任意两边的和大于第三边;三角形任意两边之差小于第三边。
3.判断三条线段能否围成三角形,只要把最短的两条边相加与最长边比较即可,如果最短的两边之和大于第三边,三条线段就能围成三角形。
感谢观看
四年级
