浙江省五校2014届高三第二次联考数学文试题 Word版含答案
文档属性
| 名称 | 浙江省五校2014届高三第二次联考数学文试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-06 00:00:00 | ||
图片预览




文档简介
2013学年浙江省第二次五校联考
数学(文科)试题卷
第Ⅰ卷
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,且,那么的值可以是( )
A. B. C. D.
2.已知,则“”是 “”的( )
A.必要而不充分条件 B.充要条件?
C.充分而不必要条件 D.既不充分也不必要条件
3.如图是某班50位学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是:,,,,,,则图中的值等于
A. B.? C. D.
4.已知的图像与的图象的两相邻交点间的距离为要得到的图像,只需把的图像 ( )
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D. 向左平移个单位
5.下列命题正确的是( )
A.若平面不平行于平面,则内不存在直线平行于平面
B.若平面不垂直于平面,则内不存在直线垂直于平面
C.若直线不平行于平面,则内不存在直线平行于直线
D.若直线不垂直于甲面,则内不存在直线垂直于直线
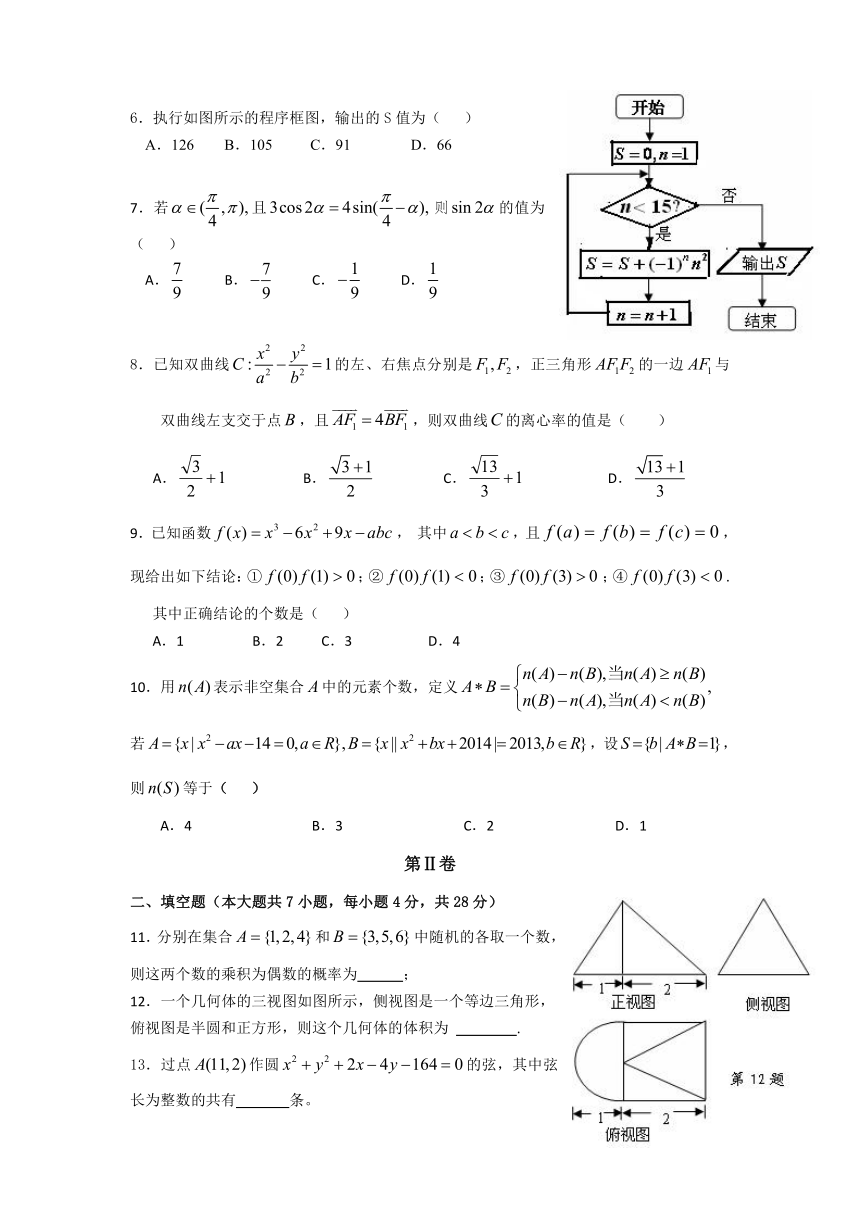
6.执行如图所示的程序框图,输出的S值为( )
A.126 B.105? C.91 D.66
7.若且则的值为 ( )
A. B. C. D.
8.已知双曲线的左、右焦点分别是,正三角形的一边与双曲线左支交于点,且,则双曲线的离心率的值是( )
A. B. C. D.
9.已知函数, 其中,且,现给出如下结论:①;②;③;④.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.用表示非空集合中的元素个数,定义
若,设,
则等于( )
A.4 B.3 C.2 D.1
第Ⅱ卷
二、填空题(本大题共7小题,每小题4分,共28分)
11.分别在集合和中随机的各取一个数,则这两个数的乘积为偶数的概率为 ;
12.一个几何体的三视图如图所示,侧视图是一个等边三角形,俯视图是半圆和正方形,则这个几何体的体积为 .
13.过点作圆的弦,其中弦长为整数的共有 条。
14.若实数满足不等式组,则的最大值是
15.已知为椭圆的左焦点,直线与椭圆交于两点,那么=
16.已知为的外心,.若, 则=
17.设,则的最小值为
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)中,三个内角A、B、C所对的边分别为、、,若,.
(Ⅰ)求角的大小;
(Ⅱ)已知的面积为,求函数的最大值.
19.(本题满分14分)已知等差数列数列的前项和为,等比数列的各项均为正数,公比是,且满足:.
(Ⅰ)求与;
(Ⅱ)设,若满足:对任意的恒成立,
求的取值范围.
20.(本题满分15分)如图,在四棱锥中,平面PAD⊥平面ABCD, ,,E是BD的中点.
(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角的的正弦值.
21.(本题满分l5分)已知函数。
(Ⅰ)若曲线在点处的切线与直线平行,求的值;
(Ⅱ)若函数在其导函数的单调区间上也是单调的,求的取值范围.
22.(本题满分14分)如图,已知过点的抛物线与过点的动直线相交于、两点.
(I)求直线与直线的斜率的乘积;
(II)若,求证:△的周长为定值.
2013学年浙江省第二次五校联考
数学(文科)答案
一、选择题: 本大题共10小题, 每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.D 2.C 3. D 4.A 5.B 6. B 7. C 8. D 9.B 10. A
二、 填空题: 本大题共7小题, 每小题4分, 共28分.
11. 12. 13.32 14.5 15. 16.3 17.
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.解:(1)因为,所以,
因为,由正弦定理可得:
,整理可得:
所以,。
(2)由得
从而=
当时,函数取得最大值。
19.解:(Ⅰ)由已知可得,消去得:,
解得或(舍),从而
(Ⅱ)由(1)知:.
∵对任意的恒成立, 即:恒成立,整理得:
对任意的恒成立,即:对任意的恒成立.
∵ 在区间上单调递增,.
的取值范围为.
20.解:(Ⅰ)如图,取PA中点F,连结EF、FD,
∵E是BP的中点,∴EF//AB且,
又∵∴EFDC∴四边形EFDC是平行四边形,故得EC//FD ……2分
又∵EC平面PAD,FD平面PAD∴EC//平面ADE …………4分
(Ⅱ)取AD中点H,连结PH,因为PA=PD,
所以PH⊥AD
∵平面PAD⊥平面ABCD于AD ∴PH⊥面ABCD
∴HB是PB在平面ABCD内的射影 ∴∠PBH是PB与平面ABCD所成角…………6分
∵四边形ABCD中,
∴四边形ABCD是直角梯形,
设AB=2a,则,在中,易得,
,又∵,
∴是等腰直角三角形,
∴
∴在中,…………10分
(Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,则HG是PG在平面ABCD上的射影,故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,由AB=2a…………11分
,又∴,
在中,
∴二面角P-AB-D的的正弦值为 …………15分
21.解:(1)
由题知,有,得或 ……4分
而当时,切线与平行,符合题意
当时,切线为重合,不合条件,舍去
故. ……………6分
(2),
设,,设的两根为
(1)当即时,,单调递增,满足题意;………8分
(2)当即或时,
①若,则,即,
此时,在上单调递减,在上单调递增,而在上单调递增,故不满足题意 …………………………10分
②若,则,
此时,在上单调递增,满足题意 ……………12分
③若,则,此时,在上单调递增,在上单调递减,在上单调递增,故不满足题意 ……………14分
综上得的取值范围为 …………………………15分
22.解:(I)由抛物线过点知………………1分
设直线的方程为
由得 ………………2分
设,
则 ………………3分
…6分
(II)的中点坐标为,即,
,
所以的中点坐标为, ………………8分
由已知得,即.………………10分
设,则,
在上是增函数,又,,故在内有一个零点,
函数有且只有一个零点,即方程有唯一实根.
所以满足条件的三角形唯一确定,从而△的周长为定值.…………14分
数学(文科)试题卷
第Ⅰ卷
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,且,那么的值可以是( )
A. B. C. D.
2.已知,则“”是 “”的( )
A.必要而不充分条件 B.充要条件?
C.充分而不必要条件 D.既不充分也不必要条件
3.如图是某班50位学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是:,,,,,,则图中的值等于
A. B.? C. D.
4.已知的图像与的图象的两相邻交点间的距离为要得到的图像,只需把的图像 ( )
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D. 向左平移个单位
5.下列命题正确的是( )
A.若平面不平行于平面,则内不存在直线平行于平面
B.若平面不垂直于平面,则内不存在直线垂直于平面
C.若直线不平行于平面,则内不存在直线平行于直线
D.若直线不垂直于甲面,则内不存在直线垂直于直线
6.执行如图所示的程序框图,输出的S值为( )
A.126 B.105? C.91 D.66
7.若且则的值为 ( )
A. B. C. D.
8.已知双曲线的左、右焦点分别是,正三角形的一边与双曲线左支交于点,且,则双曲线的离心率的值是( )
A. B. C. D.
9.已知函数, 其中,且,现给出如下结论:①;②;③;④.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.用表示非空集合中的元素个数,定义
若,设,
则等于( )
A.4 B.3 C.2 D.1
第Ⅱ卷
二、填空题(本大题共7小题,每小题4分,共28分)
11.分别在集合和中随机的各取一个数,则这两个数的乘积为偶数的概率为 ;
12.一个几何体的三视图如图所示,侧视图是一个等边三角形,俯视图是半圆和正方形,则这个几何体的体积为 .
13.过点作圆的弦,其中弦长为整数的共有 条。
14.若实数满足不等式组,则的最大值是
15.已知为椭圆的左焦点,直线与椭圆交于两点,那么=
16.已知为的外心,.若, 则=
17.设,则的最小值为
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)中,三个内角A、B、C所对的边分别为、、,若,.
(Ⅰ)求角的大小;
(Ⅱ)已知的面积为,求函数的最大值.
19.(本题满分14分)已知等差数列数列的前项和为,等比数列的各项均为正数,公比是,且满足:.
(Ⅰ)求与;
(Ⅱ)设,若满足:对任意的恒成立,
求的取值范围.
20.(本题满分15分)如图,在四棱锥中,平面PAD⊥平面ABCD, ,,E是BD的中点.
(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角的的正弦值.
21.(本题满分l5分)已知函数。
(Ⅰ)若曲线在点处的切线与直线平行,求的值;
(Ⅱ)若函数在其导函数的单调区间上也是单调的,求的取值范围.
22.(本题满分14分)如图,已知过点的抛物线与过点的动直线相交于、两点.
(I)求直线与直线的斜率的乘积;
(II)若,求证:△的周长为定值.
2013学年浙江省第二次五校联考
数学(文科)答案
一、选择题: 本大题共10小题, 每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.D 2.C 3. D 4.A 5.B 6. B 7. C 8. D 9.B 10. A
二、 填空题: 本大题共7小题, 每小题4分, 共28分.
11. 12. 13.32 14.5 15. 16.3 17.
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.解:(1)因为,所以,
因为,由正弦定理可得:
,整理可得:
所以,。
(2)由得
从而=
当时,函数取得最大值。
19.解:(Ⅰ)由已知可得,消去得:,
解得或(舍),从而
(Ⅱ)由(1)知:.
∵对任意的恒成立, 即:恒成立,整理得:
对任意的恒成立,即:对任意的恒成立.
∵ 在区间上单调递增,.
的取值范围为.
20.解:(Ⅰ)如图,取PA中点F,连结EF、FD,
∵E是BP的中点,∴EF//AB且,
又∵∴EFDC∴四边形EFDC是平行四边形,故得EC//FD ……2分
又∵EC平面PAD,FD平面PAD∴EC//平面ADE …………4分
(Ⅱ)取AD中点H,连结PH,因为PA=PD,
所以PH⊥AD
∵平面PAD⊥平面ABCD于AD ∴PH⊥面ABCD
∴HB是PB在平面ABCD内的射影 ∴∠PBH是PB与平面ABCD所成角…………6分
∵四边形ABCD中,
∴四边形ABCD是直角梯形,
设AB=2a,则,在中,易得,
,又∵,
∴是等腰直角三角形,
∴
∴在中,…………10分
(Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,则HG是PG在平面ABCD上的射影,故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,由AB=2a…………11分
,又∴,
在中,
∴二面角P-AB-D的的正弦值为 …………15分
21.解:(1)
由题知,有,得或 ……4分
而当时,切线与平行,符合题意
当时,切线为重合,不合条件,舍去
故. ……………6分
(2),
设,,设的两根为
(1)当即时,,单调递增,满足题意;………8分
(2)当即或时,
①若,则,即,
此时,在上单调递减,在上单调递增,而在上单调递增,故不满足题意 …………………………10分
②若,则,
此时,在上单调递增,满足题意 ……………12分
③若,则,此时,在上单调递增,在上单调递减,在上单调递增,故不满足题意 ……………14分
综上得的取值范围为 …………………………15分
22.解:(I)由抛物线过点知………………1分
设直线的方程为
由得 ………………2分
设,
则 ………………3分
…6分
(II)的中点坐标为,即,
,
所以的中点坐标为, ………………8分
由已知得,即.………………10分
设,则,
在上是增函数,又,,故在内有一个零点,
函数有且只有一个零点,即方程有唯一实根.
所以满足条件的三角形唯一确定,从而△的周长为定值.…………14分
同课章节目录
