不等关系[下学期]

课件22张PPT。生产日期：2003.05.11
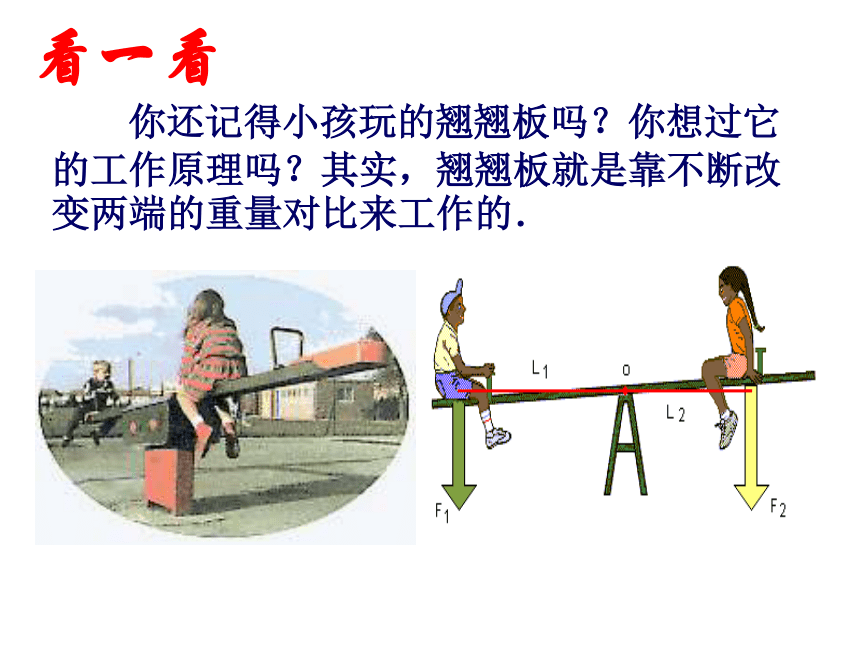
保质期： 6个月警告！为了你的生命安全，燃放时请及时转移至5米之外。 你还记得小孩玩的翘翘板吗？你想过它的工作原理吗？其实，翘翘板就是靠不断改变两端的重量对比来工作的．
看一看　在古代，我们的祖先就懂得了翘翘板的工作原理，并且根据这一原理设计出了一些简单机械，并把它们用到了生活实践当中．
由此可见，“不相等”处处可见。从今天起，我们开始学习一类新的数学知识：不等式．
不等关系不相等 处处可见不等式不等号的类型： （1）“≠”读作“不等于”，它说明两个量之间的关系是不相等的，但不能明确两个量谁大谁小；
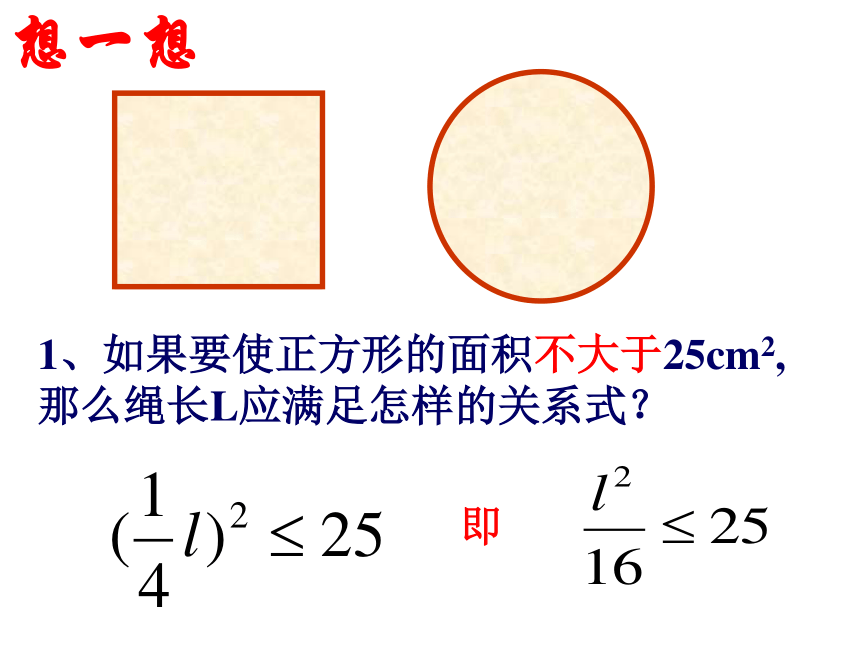
（2）“＞”读作“大于”，它表示其左边的数比其右边的数大； （3）“＜”读作“小于”，它表示其左边的数比其右边的数小； （4）“≥”读作“大于或等于”，它的意义是指左边的数不小于右边的数； （5）“≤”读作“小于或等于”，它的意义是指左边的数不大于右边的数。 想一想 在抗击“非典”时期，市实验中学准备在学校饭厅楼道处新添设一个通风口，四周用长为Lcm的装潢条镶嵌（不计接缝），八年级（1）班数学研究性学习小组设计了两种方案，如下图： 1、如果要使正方形的面积不大于25cm2,那么绳长L应满足怎样的关系式？
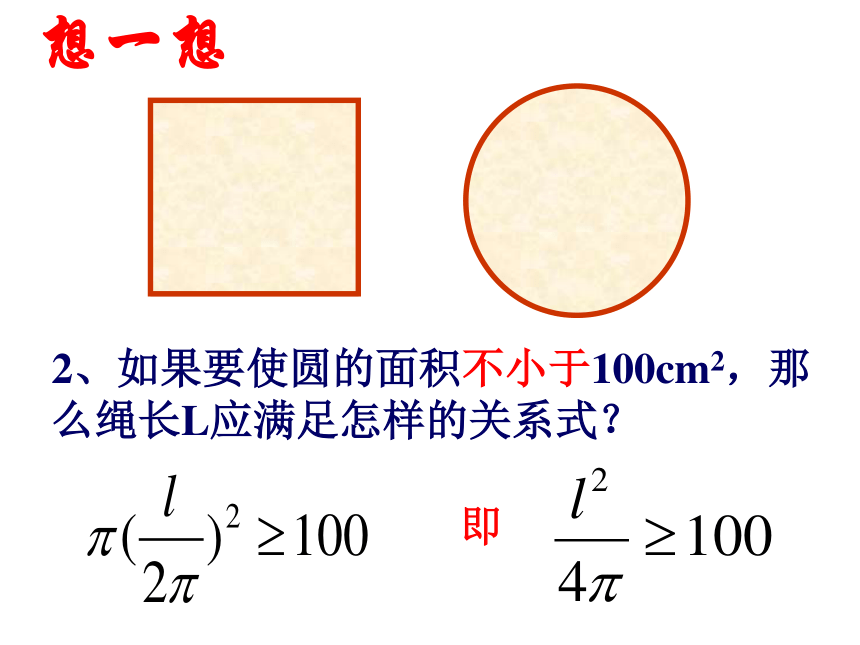
想一想即2、如果要使圆的面积不小于100cm2，那么绳长L应满足怎样的关系式？
想一想即3、当L= 8时，正方形和圆的面积哪个大？ L = 12呢？
想一想当L=8时，所以，当L=8时，当L=12时，4、你能得到什么猜想？改变 L的取值再试一试。
想一想猜想：无论L取何值，圆的面积总大于正方形的面积。5、经过探究，你应该选择哪种设计方案？请说明理由 做一做： 通过测量一棵树的树围（树干的周长）可以计算出它的树龄，通常规定以树干离地面1.5cm的地方作为测量部位。某树栽种时的树围为5cm，以后树围每年增加约3cm。这棵树至少生长多少年其树围才能超过2.4m？解：设这棵树生长x年其树围才能超过2.4m， 根据题意得：5＋3x＞240议一议 观察由上述问题得到的如下关系式，它们有什么共同特点？ 共同点：这些关系式都是用不等号连接的式子 一般地，用符号“＜”（或“≤”），“＞” （或“≥”）连接的式子叫作不等式
?
(1)≤ 25(2)≥100(3)＞(4)5＋3x＞240用适当的符号表示下列关系： 1. x与7的差是正数； 2. a是非负数； 3. a的2倍与3的和大于1； 4. 5a-4不超过3-2a； 牛刀小试x-7＞0 a≥0 2a+3＞1 5a-4≤3-2a 变式：当x=2时，不等式x-7 ＞0成立吗？想一想：团体至少多少人时，多买票反而合算呢？ 1、玄武湖公园的票价是每人5元；一次购买票满30张，每张可少收1元。某班有27名少先队员去玄武湖举行活动，当领队刘老师准备好了零钱到售票处买27张票时，爱动脑筋的小刚同学喊住了刘老师，提议买30张票。但有的同学不明白，明明我们只有27人，买30张票，岂不是“浪费”吗？小刚的提议对不对？是否真的“浪费”吗？你能解释其中的道理吗？
请你决策2、 有6个实数： ， ， ，0， ,
.请你写出其中两数和不超过10的数组.（写出两组即可）
与与 0与3、a、b两个实数在数轴上的对应点如下图所示： · · ·
b 0 a
用“”或“”填空：
（1）a_____b （2）︱a︱____︱b︱
（3）a+b____0 （4）a-b_____0
（5）a+b____a-b （6）ab______a
4、为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表： 经核算，该企业购买设备的资金不高于105万元，若购买A型设备x台. （1）试写出x应满足的关系式； （2）若企业每月产生的污水量为2040t，那么你能写出x（台）应满足的另一个不等式吗？ 反馈测试：
1、用不等式表示：
（1）比－3大但比5小的数；
（2）不小于－5的非负正数. 解：设满足条件的数为x，则（1）-3＜x＜5 （2）－5≤x≤0
2、振兴小学学生陈华和他的爸爸、妈妈准备在“五一”外出旅游，春光旅行社的收费标准为：大人全价，小孩半价；而华夏旅行社不管大人小孩，一律八折.若这两家旅行社的基本价一样，你认为陈华一家选哪家旅行社较合算. 解：设每人的基本价为a元，则
春光旅行社的总收费为：2a＋a×50﹪=2.5a
华夏旅行社的总收费为：3a×80﹪=2.4a ∵a＞0 ∴2.5a＞2.4a
因此，陈华一家选华夏旅行社较合算 B＜A＜C