1.2不等式的基本性质[下学期]

课件20张PPT。 第二节
不等式的基本性质一、学前练习 1. -7 ≤ -5, 3+4＞1+4
5+3≠12-5, x ≥ 8
a+2＞a+1， x+3 ＜6

(1)上述式子有哪些表示数量关系的符号？
这些符号表示什么关系？
(2)这些符号两侧的代数式可随意交换
位置吗？
(3)什么叫不等式？ （表示不等关系）（不可随意互换位置）（用不等号表示不等关系的式子叫不等式）二、探究新知：
1. 商场A种服装的价格为60元，B种服装的价格为80元
（1）两种服装都涨价10元，哪种服装价格高？涨价15元呢？
（2）两种服装都降价5元，哪种服装价格高？降价15元呢？
（3）两种服装都打8折出售，哪种服装价格高？2.已知 4 > 3，填空：
4×（-1）——3 ×（-1）
4×（-5）——3 ×（-5）不等式的基本性质性质1，不等式的两边都加上（或减去）
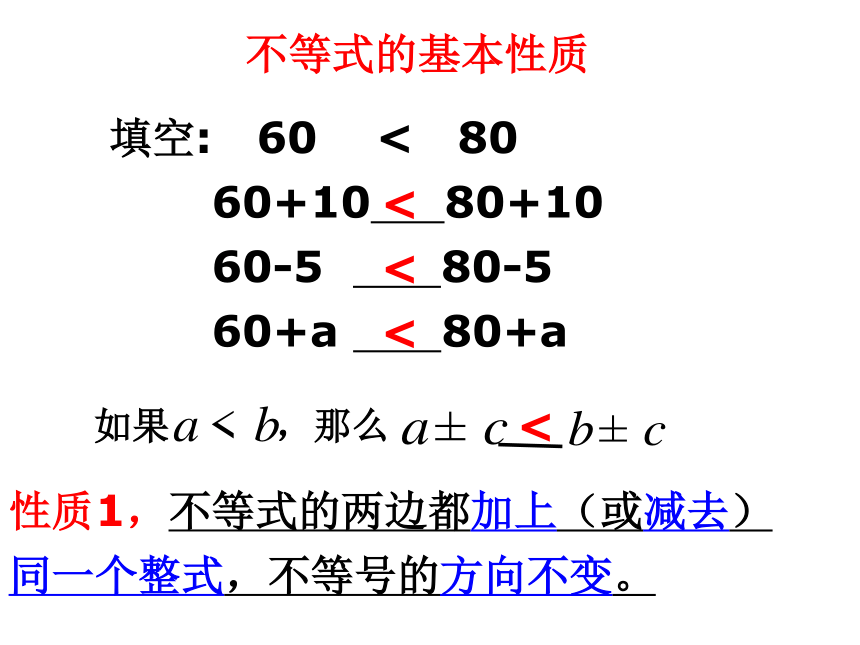
同一个整式，不等号的方向不变。填空: 60 < 80
60+10 80+10
60-5 80-5
60+a 80+a如果 ，那么<60 ×0.8 80 ×0.8不等式的基本性质性质2，不等式的两边都乘以（或除以）
同一个正数，不等号的方向不变。 4 > 3
4×5 3×5
4÷2 3÷2如果a>b，c>0 ，那么ac>bc，60 < 80<填空(1)：填空(2)：不等式的基本性质性质3，不等式的两边都乘以（或除以）
同一个负数，不等号的方向改变。填空： 4 > 3
4×(-1) 3×(-1)
4×(-5) 3×(-5)
4÷(-2) 3÷(-2)如果a>b，c<0 ，那么ac 不等式的三条基本性质
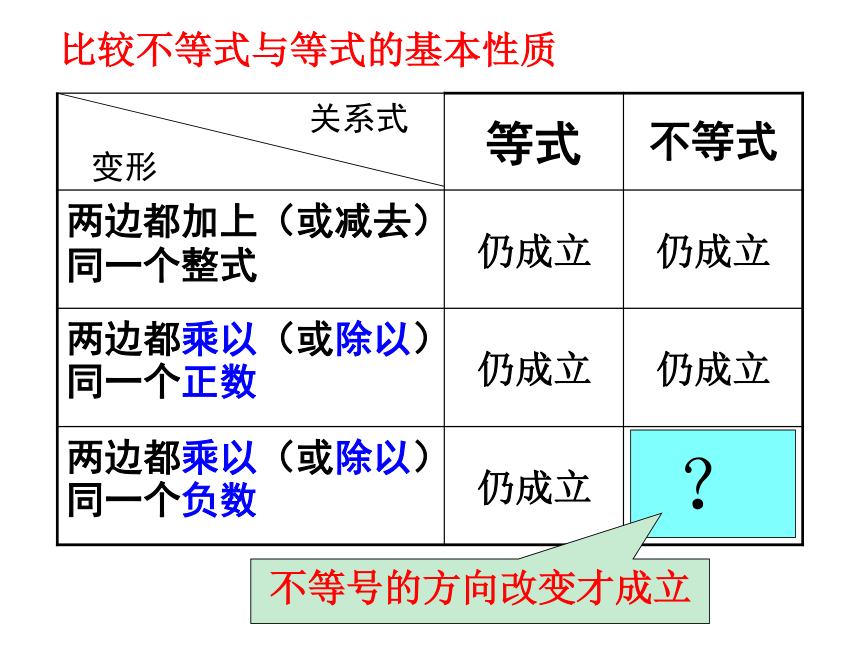
1. 不等式两边都加上（或减去）同一个
数或同一个整式，不等号的方向不变；
2. 不等式两边都乘（或除以）同一个
正数，不等号的方向不变；
3.*不等式两边都乘（或除以）同一个
负数，不等号的方向改变 ；---如何用数学语言表示？
---与等式的基本性质有什么联系与区别？？不等号的方向改变才成立比较不等式与等式的基本性质 解：(1)根据不等式基本性质1，两边都加上2，
得： x-2+2＜3+2
x＜5
(2)根据不等式基本性质1，两边都减去5x，
得： 6x-5x＜5x-1-5x
x＜-1四、典型例题：
例1.根据不等式的基本性质，把下列不等式化成x＜a或x＞a的形式：
(1) x-2＜ 3 (2) 6x＜ 5x-1
(3) 1/2 x＞5 (4) -4x＞3 例2.设a＞b，用“＜”或“＞”填空：
(1)a-3 b-3 (2) (3) -4a -4b解:(1) ∵a＞b
∴两边都减去3，由不等式基本性质1
得 a-3＞b-3
(2) ∵a＞b，并且2＞0
∴两边都除以2，由不等式基本性质2
得 (3) ∵a＞b，并且-4＜0
∴两边都乘以-4，由不等式基本性质3
得 -4a＜-4b五、变式训练：
1、已知x＜y,用“＜”或“＞”填空。
（1）x+2 y+2 （不等式的基本性质 ）
(2) x y （不等式的基本性质 ）
（3）－x －y （不等式的基本性质 ）
(4)x－m y－m （不等式的基本性质 ） 　　　　　　　　　　　　　　　 1.用“＞”或“＜”在横线上填空，并在题后
括号内填写理由.
∵a＞b (2)∵ a＞b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m＞5n (4)∵4x＞5x
∴ -m ( ) ∴ x 0( )
(5)∵ ＜ (6)∵a-1＜8
∴ a 2b( ) ∴ a 9( ) ＞＞＞＜＜＜不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质12、若a-b<0，则下列各式中一定成立
的是（ ）
A.a>b B.ab>0
C. D.-a>-b
3、若x是任意实数，则下列不等式中，
恒成立的是（ ）
A.3x>2x B.3x2>2x2
C.3+x>2 D.3+x2>2DD 4、单项选择：
(1)由 x＞y 得 ax＞ay 的条件是（ ）
A.a ≥0 B.a ＞ 0 C.a＜ 0 D.a≤0
(2)由 x＞y 得 ax≤ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
(3)由 a＞b 得 am2＞bm2 的条件是（ ）
A.m＞0 B.m＜0 C.m≠0 D.m是任意有理数
(4)若 a＞1，则下列各式中错误的是（ ）
A.4a＞4 B.a+5＞6 C. ＜ D.a-1＜0BDCD 5、判断正误：
(1)∵a+8＞4 (2)∵3＞2
∴a＞-4 ( ) ∴3a＞2a( )
(3)∵-1＞-2 (4)∵ab＞0
∴a-1＞a-2 ( ) ∴a＞0,b＞ 0( )√×√×6、下列各题是否正确?请说明理由(1)如果a＞b,那么ac＞bc(2)如果a＞b,那么ac2 ＞bc2
(3)如果ac2＞bc2,那么a＞b(4)如果a＞b,那么a-b＞0(5)如果ax＞b且a≠0,那么x＞b/a7、利用不等式的基本性质填空,
(填“＜”或“＞”)
（1）若a＞b，则2a+1 2b+1，
（2）若－ y＜10，则y －8，
（3）若a＜b，且c＞0，则
ac+c bc+ c，
（4）若a＞0，b＜0，c＜0，则
（a－b）c 0。8、试一试：(1) 2a和a+1(2)2a和a-1比较2a与a的大小(1)当a>0时，2a>a；
(2)当a=0时，2a=a；
(3)当a<0时，2a 1.本节重点
(1)掌握不等式的三条基本性质，尤其是性质3；
(2)能正确应用性质对不等式进行变形；
2.注意事项
（1）要反复对比不等式性质与等式性质
的异同点；
（2）当不等式两边都乘以（或除以）同
一个数时，一定要看清是正数还是
负数；对于未给定范围的字母，应
分情况讨论.