2022—2023学年人教版数学七年级下册5.2.2平行线的判定 课件(共14张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级下册5.2.2平行线的判定 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 954.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
习 惯 指 标
★做好课前准备
第五章相交线与平行线
5.2.2 平行线的判定
初探·自学
知识回顾
★积极参与课堂合作
习惯指标
问题1:平行线有哪些判定方法?
(3)同位角相等,两直线平行.
(4)内错角相等,两直线平行.
(5)同旁内角互补,两直线平行.
(1)定义.
(2)平行公理的推论 若a//b,b//c,则a//c.
初探·自学
课前预行线的判定
学科指标
★积极参与课堂合作
习惯指标
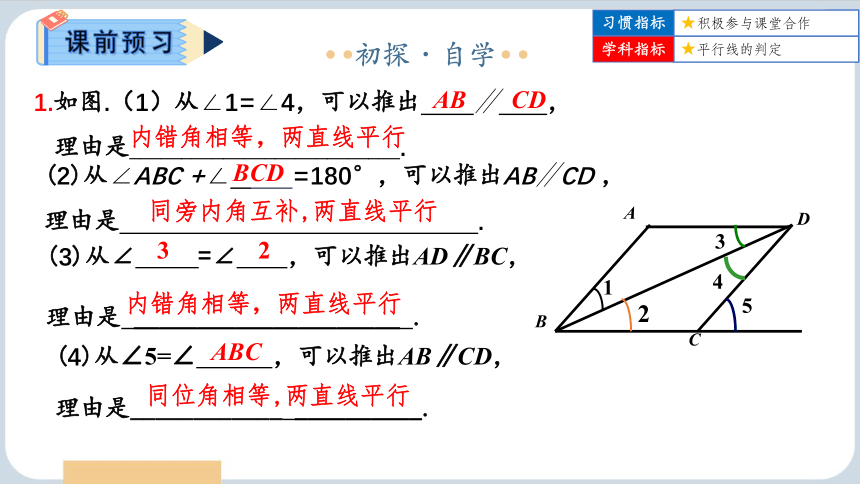
1.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是__________________________.
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 _____________________ .
(4)从∠5=∠ ,可以推出AB∥CD,
理由是____________ __________.
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
初探·自学
课前预行线的判定
学科指标
★积极参与课堂合作
习惯指标
① ∵ ∠1 =_____(已知),
∴ AB∥CE( );
② ∵ ∠1 +_____=180o(已知),
∴CD∥BF( );
③ ∵ ∠1 +∠5 =180o(已知),
∴ ___∥_____( );
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
2.根据条件完成填空:
合探·自学
例题讲解
★平行线的性质
学科指标
★积极参与课堂合作
习惯指标
理由如下:
∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知) ,
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
例1 如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
解: AB∥CD.
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
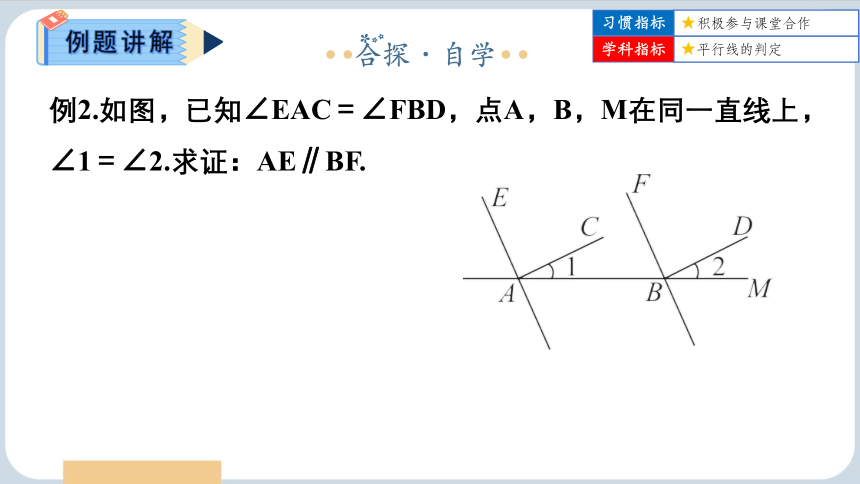
例2.如图,已知∠EAC=∠FBD,点A,B,M在同一直线上,∠1=∠2.求证:AE∥BF.
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
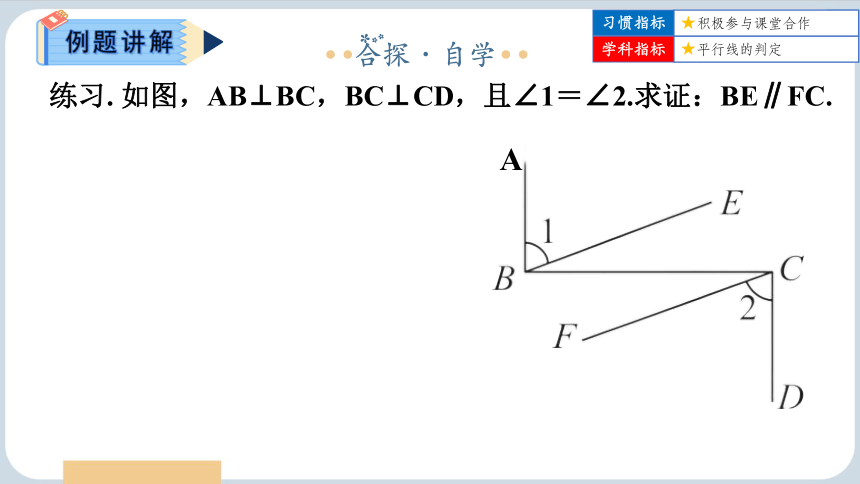
练习. 如图,AB⊥BC,BC⊥CD,且∠1=∠2.求证:BE∥FC.
A
合探·自学
探究新知
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例3.如图,AB⊥BC,∠1+∠2=90°,∠2=∠3.求证:BE∥DF.
合探·自学
探究新知
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例4 将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;(2)求∠DFC的度数.
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例5 如图,一辆汽车而经过两次拐弯之后,驶方向与原来平行,若第一次是向左拐40°,则第二次拐弯的角度是( )
A.右拐40° B.左拐40° C.左拐140° D.右拐140°
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
练习.一辆汽车笔直行驶,它( )之后,行驶的路线与原来平行,行驶的方向与原来相反.
A.先左拐30°再右拐150° B.先左拐150°再左拐30°
C.先左拐30°再左拐30° D.先右拐30°再右拐30°
例6.一辆汽车笔直行驶,它( )之后,行驶的路线与原来平行,行驶的方向与原来相同.
A.先左拐30°再右拐150° B.先左拐150°再右拐30°
C.先左拐30°再左拐30° D.先左拐30°再右拐30°
深探·自学
拓展提升
★平行线的性质
学科指标
★积极参与课堂合作
习惯指标
例6.如图,AF分别与BD、CE交于点G、H,AC分别与BD、CE交于
点B、C,DF分别与BD、CE交于点D、E,若∠A=∠F,∠C=∠D,∠1=55°.求∠2的度数.
深探·自学
拓展提升
★平行线的性质
学科指标
★积极参与课堂合作
习惯指标
例7.已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠ACB=∠4.
证明:∵∠1+∠DFE=180°( ),
又∵∠1+∠2=180°(已知),
∴∠2=∠DFE( ),
∴AB∥EF( ),
∴∠3=∠_________.
∵∠3=∠B(已知),
∴∠B=∠_________,
∴DE∥BC( ),
∴∠ACB=∠4( ).
谢谢大家
万物皆有裂痕,那是光进来的地方.
习 惯 指 标
★做好课前准备
第五章相交线与平行线
5.2.2 平行线的判定
初探·自学
知识回顾
★积极参与课堂合作
习惯指标
问题1:平行线有哪些判定方法?
(3)同位角相等,两直线平行.
(4)内错角相等,两直线平行.
(5)同旁内角互补,两直线平行.
(1)定义.
(2)平行公理的推论 若a//b,b//c,则a//c.
初探·自学
课前预行线的判定
学科指标
★积极参与课堂合作
习惯指标
1.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是__________________________.
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 _____________________ .
(4)从∠5=∠ ,可以推出AB∥CD,
理由是____________ __________.
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
初探·自学
课前预行线的判定
学科指标
★积极参与课堂合作
习惯指标
① ∵ ∠1 =_____(已知),
∴ AB∥CE( );
② ∵ ∠1 +_____=180o(已知),
∴CD∥BF( );
③ ∵ ∠1 +∠5 =180o(已知),
∴ ___∥_____( );
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
2.根据条件完成填空:
合探·自学
例题讲解
★平行线的性质
学科指标
★积极参与课堂合作
习惯指标
理由如下:
∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知) ,
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
例1 如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
解: AB∥CD.
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例2.如图,已知∠EAC=∠FBD,点A,B,M在同一直线上,∠1=∠2.求证:AE∥BF.
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
练习. 如图,AB⊥BC,BC⊥CD,且∠1=∠2.求证:BE∥FC.
A
合探·自学
探究新知
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例3.如图,AB⊥BC,∠1+∠2=90°,∠2=∠3.求证:BE∥DF.
合探·自学
探究新知
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例4 将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;(2)求∠DFC的度数.
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
例5 如图,一辆汽车而经过两次拐弯之后,驶方向与原来平行,若第一次是向左拐40°,则第二次拐弯的角度是( )
A.右拐40° B.左拐40° C.左拐140° D.右拐140°
合探·自学
例题讲解
★平行线的判定
学科指标
★积极参与课堂合作
习惯指标
练习.一辆汽车笔直行驶,它( )之后,行驶的路线与原来平行,行驶的方向与原来相反.
A.先左拐30°再右拐150° B.先左拐150°再左拐30°
C.先左拐30°再左拐30° D.先右拐30°再右拐30°
例6.一辆汽车笔直行驶,它( )之后,行驶的路线与原来平行,行驶的方向与原来相同.
A.先左拐30°再右拐150° B.先左拐150°再右拐30°
C.先左拐30°再左拐30° D.先左拐30°再右拐30°
深探·自学
拓展提升
★平行线的性质
学科指标
★积极参与课堂合作
习惯指标
例6.如图,AF分别与BD、CE交于点G、H,AC分别与BD、CE交于
点B、C,DF分别与BD、CE交于点D、E,若∠A=∠F,∠C=∠D,∠1=55°.求∠2的度数.
深探·自学
拓展提升
★平行线的性质
学科指标
★积极参与课堂合作
习惯指标
例7.已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠ACB=∠4.
证明:∵∠1+∠DFE=180°( ),
又∵∠1+∠2=180°(已知),
∴∠2=∠DFE( ),
∴AB∥EF( ),
∴∠3=∠_________.
∵∠3=∠B(已知),
∴∠B=∠_________,
∴DE∥BC( ),
∴∠ACB=∠4( ).
谢谢大家
万物皆有裂痕,那是光进来的地方.
