华东师大版数学八年级下册18.2 第1课时 从边判定平行四边形课时练习(含答案)
文档属性
| 名称 | 华东师大版数学八年级下册18.2 第1课时 从边判定平行四边形课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 00:00:00 | ||
图片预览


文档简介
18.2 第1课时 从边判定平行四边形
一、选择题
1.下列条件中能判定四边形ABCD是平行四边形的是 ( )
A.AB∥CD,AB=CD
B.AB=BC,AD=CD
C.AC=BD,AB=CD
D.AB∥CD,AD=CB
2.如图1,在四边形ABCD中,AB=CD,BC=AD.若∠D=120°,则∠C的度数为 ( )
图1
A.60° B.70° C.80° D.90°
3.在四边形ABCD中,①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从以上条件中选择两个使四边形ABCD为平行四边形的选法共有 ( )
A.3种 B.4种 C.5种 D.6种
4.如图2,在四边形ABCD中,AB∥CD,添加下列条件,仍不能判定四边形ABCD是平行四边形的是 ( )
图2
A.AB=CD B.BC∥AD
C.∠A=∠C D.BC=AD
5.如图3,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
图3
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE
二、填空题
6.如图,A是直线l外一点,在l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径画弧,两弧交于点D,连结AB,AD,CD,则四边形ABCD一定是 .
7.横格纸的横线是互相平行的,在一条横线上截取线段AB= 25 mm,在另一条横线上按照同一方向截取CD=25 mm,连结AC,BD,那么四边形ACDB一定是平行四边形,理由是 .
8.如图4,D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连结CD,BC,则四边形ABCD是平行四边形,理由是 .
图4
9.如图5,为了体验四边形的不稳定性,将四根木条用钉子钉成一个四边形框架ABCD,且AB=CD,AD=BC,B,D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,给出如下4种说法:
①四边形ABCD为平行四边形;
②BD的长度增大;
③四边形ABCD的面积不变;
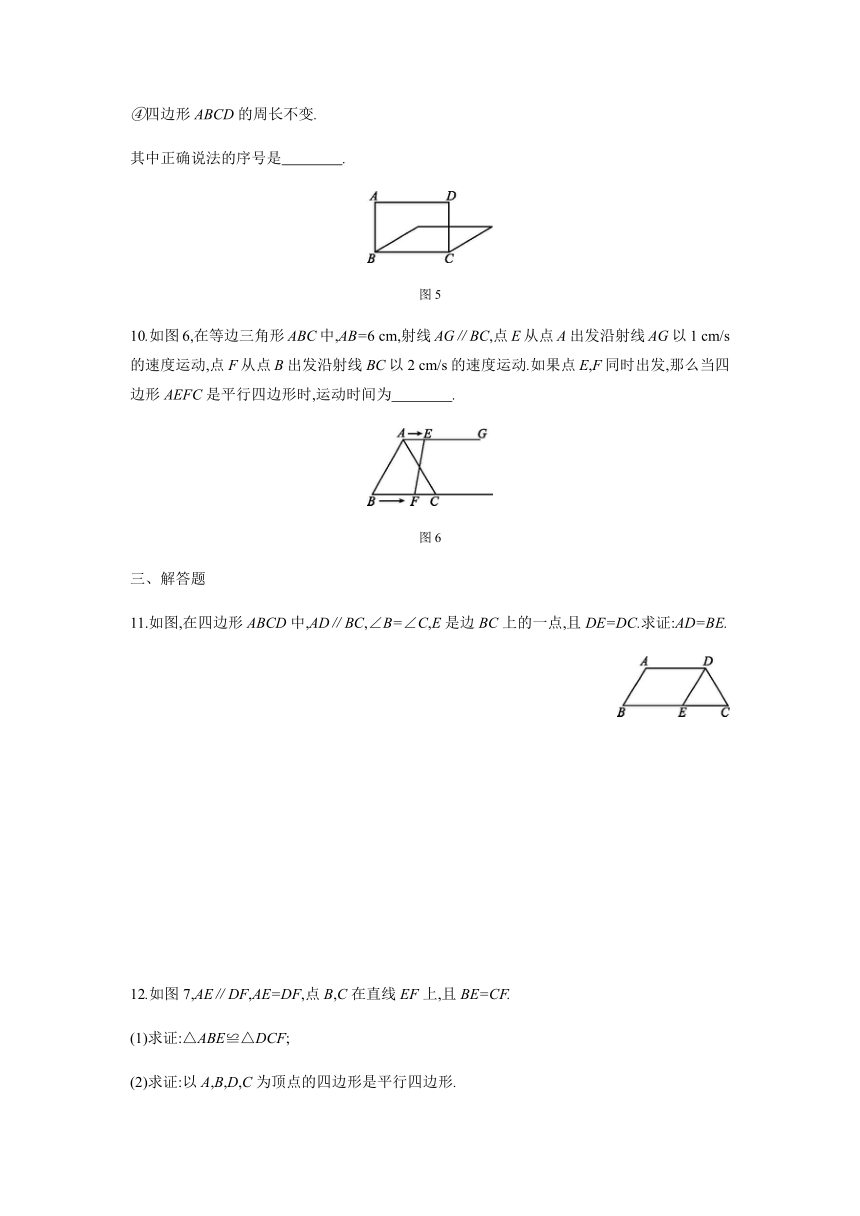
④四边形ABCD的周长不变.
其中正确说法的序号是 .
图5
10.如图6,在等边三角形ABC中,AB=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,那么当四边形AEFC是平行四边形时,运动时间为 .
图6
三、解答题
11.如图,在四边形ABCD中,AD∥BC,∠B=∠C,E是边BC上的一点,且DE=DC.求证:AD=BE.
12.如图7,AE∥DF,AE=DF,点B,C在直线EF上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)求证:以A,B,D,C为顶点的四边形是平行四边形.
图7
13.如图8,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE.
求证:AF=CE.
图8
14.如图9所示,在 ABCD中,E,F,G,H分别是四条边上的点,且AE=CF,BG=DH.
求证:EF与GH互相平分.
图9
15如图10所示,在△ABC中,E,F两点在AB边上,AE=BF,EH∥AC∥FG,H,G两点在BC边上,则线段EH,FG,AC之间有什么数量关系 试证明你的结论.
图10
参考答案
1.A 2.A 3.B 4.D 5.D
6.平行四边形
7.一组对边平行且相等的四边形是平行四边形
8.两组对边分别相等的四边形是平行四边形
9.①②④
10.6 s .
11.证明:∵DE=DC,∴∠DEC=∠C.
又∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE.
又∵AD∥BC,∴四边形ABED是平行四边形,
∴AD=BE.
12.证明:(1)∵AE∥DF,∴∠AEF=∠DFE,
∴∠AEB=∠DFC.
又∵AE=DF,BE=CF,
∴△ABE≌△DCF.
(2)连结AC,BD.∵△ABE≌△DCF,
∴AB=DC,∠ABE=∠DCF,
∴AB∥DC,
∴四边形ABDC是平行四边形.
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF.
在△ABE和△CDF中,
∵∠ABE=∠CDF,∠AEB=∠CFD,AB=CD,
∴△ABE≌△CDF,∴AE=CF.
又∵AE∥CF,∴四边形AECF是平行四边形,
∴AF=CE.
14.证明:如图,连结FG,GE,HE,HF.
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∵BG=DH,
∴AH=CG.
又∵AE=CF,∴△AEH≌△CFG,
∴HE=GF.
同理可证GE=HF,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分.
15解:AC=EH+FG.
证明:如图,过点E作ED∥BC,交AC于点D,
则∠ADE=∠C.
∵EH∥AC∥FG,
∴∠C=∠FGB,∠GFB=∠A,
∴∠ADE=∠FGB.
又∵AE=FB,
∴△ADE≌△FGB,
∴AD=FG.
∵AC∥EH,ED∥BC,
∴四边形DEHC为平行四边形,
∴DC=EH.
∵AC=DC+AD,∴AC=EH+FG.
一、选择题
1.下列条件中能判定四边形ABCD是平行四边形的是 ( )
A.AB∥CD,AB=CD
B.AB=BC,AD=CD
C.AC=BD,AB=CD
D.AB∥CD,AD=CB
2.如图1,在四边形ABCD中,AB=CD,BC=AD.若∠D=120°,则∠C的度数为 ( )
图1
A.60° B.70° C.80° D.90°
3.在四边形ABCD中,①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从以上条件中选择两个使四边形ABCD为平行四边形的选法共有 ( )
A.3种 B.4种 C.5种 D.6种
4.如图2,在四边形ABCD中,AB∥CD,添加下列条件,仍不能判定四边形ABCD是平行四边形的是 ( )
图2
A.AB=CD B.BC∥AD
C.∠A=∠C D.BC=AD
5.如图3,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
图3
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE
二、填空题
6.如图,A是直线l外一点,在l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径画弧,两弧交于点D,连结AB,AD,CD,则四边形ABCD一定是 .
7.横格纸的横线是互相平行的,在一条横线上截取线段AB= 25 mm,在另一条横线上按照同一方向截取CD=25 mm,连结AC,BD,那么四边形ACDB一定是平行四边形,理由是 .
8.如图4,D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连结CD,BC,则四边形ABCD是平行四边形,理由是 .
图4
9.如图5,为了体验四边形的不稳定性,将四根木条用钉子钉成一个四边形框架ABCD,且AB=CD,AD=BC,B,D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,给出如下4种说法:
①四边形ABCD为平行四边形;
②BD的长度增大;
③四边形ABCD的面积不变;
④四边形ABCD的周长不变.
其中正确说法的序号是 .
图5
10.如图6,在等边三角形ABC中,AB=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,那么当四边形AEFC是平行四边形时,运动时间为 .
图6
三、解答题
11.如图,在四边形ABCD中,AD∥BC,∠B=∠C,E是边BC上的一点,且DE=DC.求证:AD=BE.
12.如图7,AE∥DF,AE=DF,点B,C在直线EF上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)求证:以A,B,D,C为顶点的四边形是平行四边形.
图7
13.如图8,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE.
求证:AF=CE.
图8
14.如图9所示,在 ABCD中,E,F,G,H分别是四条边上的点,且AE=CF,BG=DH.
求证:EF与GH互相平分.
图9
15如图10所示,在△ABC中,E,F两点在AB边上,AE=BF,EH∥AC∥FG,H,G两点在BC边上,则线段EH,FG,AC之间有什么数量关系 试证明你的结论.
图10
参考答案
1.A 2.A 3.B 4.D 5.D
6.平行四边形
7.一组对边平行且相等的四边形是平行四边形
8.两组对边分别相等的四边形是平行四边形
9.①②④
10.6 s .
11.证明:∵DE=DC,∴∠DEC=∠C.
又∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE.
又∵AD∥BC,∴四边形ABED是平行四边形,
∴AD=BE.
12.证明:(1)∵AE∥DF,∴∠AEF=∠DFE,
∴∠AEB=∠DFC.
又∵AE=DF,BE=CF,
∴△ABE≌△DCF.
(2)连结AC,BD.∵△ABE≌△DCF,
∴AB=DC,∠ABE=∠DCF,
∴AB∥DC,
∴四边形ABDC是平行四边形.
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF.
在△ABE和△CDF中,
∵∠ABE=∠CDF,∠AEB=∠CFD,AB=CD,
∴△ABE≌△CDF,∴AE=CF.
又∵AE∥CF,∴四边形AECF是平行四边形,
∴AF=CE.
14.证明:如图,连结FG,GE,HE,HF.
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∵BG=DH,
∴AH=CG.
又∵AE=CF,∴△AEH≌△CFG,
∴HE=GF.
同理可证GE=HF,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分.
15解:AC=EH+FG.
证明:如图,过点E作ED∥BC,交AC于点D,
则∠ADE=∠C.
∵EH∥AC∥FG,
∴∠C=∠FGB,∠GFB=∠A,
∴∠ADE=∠FGB.
又∵AE=FB,
∴△ADE≌△FGB,
∴AD=FG.
∵AC∥EH,ED∥BC,
∴四边形DEHC为平行四边形,
∴DC=EH.
∵AC=DC+AD,∴AC=EH+FG.
