第18章 平行四边形章末复习 华师版数学八年级下册上课课件(18张PPT)
文档属性
| 名称 | 第18章 平行四边形章末复习 华师版数学八年级下册上课课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 09:50:23 | ||
图片预览




文档简介
(共18张PPT)
章末复习
华东师大版八年级数学下册
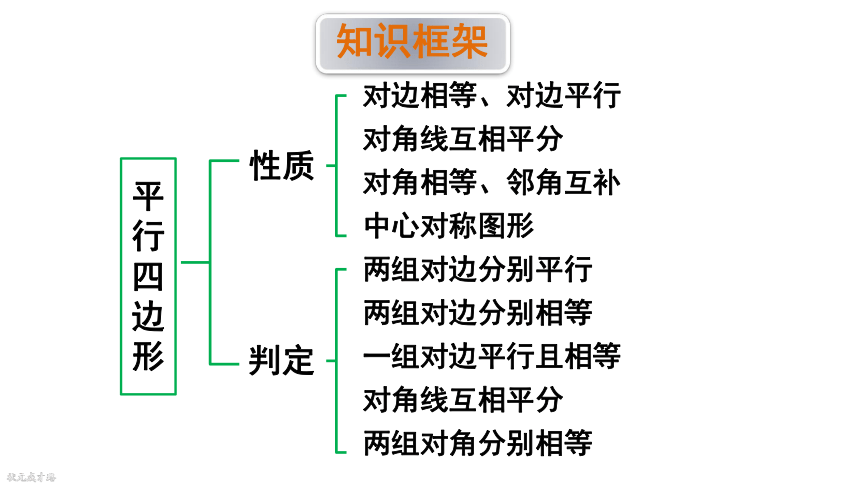
知识框架
平行四边形
对边相等、对边平行
对角线互相平分
对角相等、邻角互补
中心对称图形
两组对边分别平行
两组对边分别相等
一组对边平行且相等
对角线互相平分
两组对角分别相等
性质
判定
知识梳理
平行四边形的性质定理:
平行四边形的性质定理 1 平行四边形的对边相等.
平行四边形的性质定理 2 平行四边形的对角相等.
性
质
平行线的性质:
平行线之间的距离处处相等.
平行线的性质定理 3 平行四边形的对角线互相平分.
判
定
1. 两组对边分别平行的四边形是平行四边形
2. 两组对边分别相等的四边形是平行四边形
3. 一组对边平行且相等的四边形是平行四边形
4. 两组对角分别相等的四边形是平行四边形
5.两条对角线互相平分的四边形是平行四边形
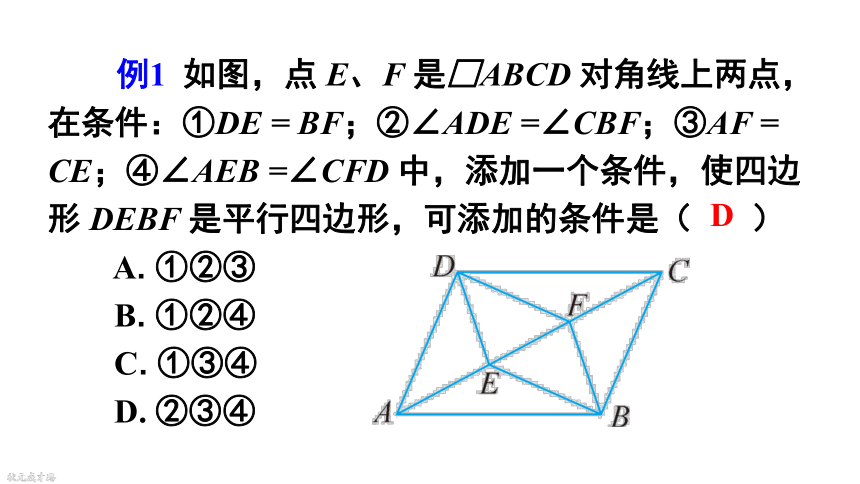
例1 如图,点 E、F 是□ABCD 对角线上两点,在条件:①DE = BF;②∠ADE =∠CBF;③AF = CE;④∠AEB =∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加的条件是( )
A. ①②③
B. ①②④
C. ①③④
D. ②③④
D
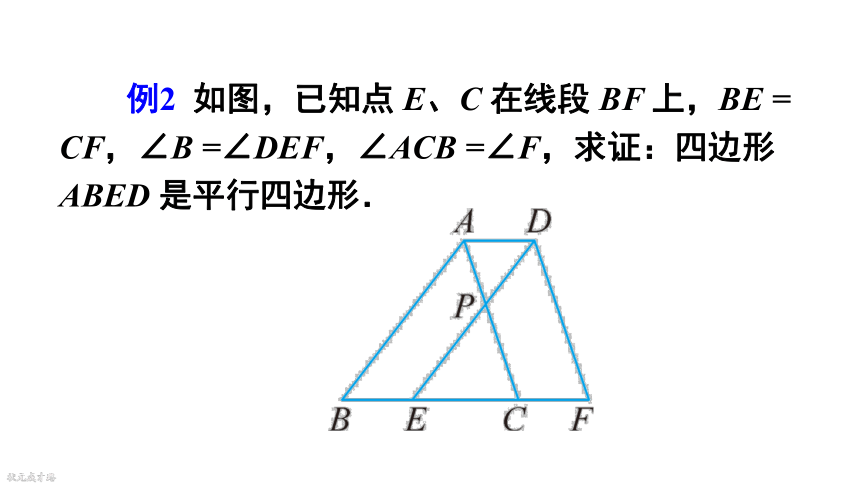
例2 如图,已知点 E、C 在线段 BF 上,BE = CF,∠B =∠DEF,∠ACB =∠F,求证:四边形ABED 是平行四边形.
证明:∵BE = CF,
∴BE + EC = CF + EC,即BC = EF,
又∵∠B =∠DEF,∠ACB =∠F,
∴△ABC ≌△DEF,
∴AB = DE,
∵∠B =∠DEF,
∴AB∥DE,
∴四边形ABED是平行四边形.
例3 如图,直线 l1∥l2,△ABC 的面积为 10,则△DBC 的面积( )
A. 大于 10
B. 小于 10
C. 等于 10
D. 不确定
l1
l2
A
B
C
D
C
例4 如图,已知 E,F 是四边形 ABCD 的对角线 AC 上的两点,AE = CF,BE = FD,BE // FD. 求证:四边形 ABCD 是平行四边形.
A
B
C
D
E
F
A
B
C
D
E
F
O
证明 连结 BF ,DE,BD与 AC 交于点 O.
∵ BE = FD,BE // FD ,
∴四边形 BEDF 是平行四边形.
∴OB = OD,OE = OF.
又∵ AE = CF ,
∴AO =CO.
∴四边形 ABCD 是平行四边形.
随堂演练
1. 如图,平行四边形 ABCD 中,∠A 的平分线 AE 交 CD 于 E,AB = 5,BC = 3,则 EC 的长是( )
A. 1 B. 2
C. 1.5 D. 3
B
2. 如图, ABCD 的对角线相交于点 O,且 AB ≠ AD,过点 O 作 OE⊥BD 交 BC于点 E. 若△CDE 的周长为 10,则 ABCD 的周长为________.
A
B
C
D
O
E
20
3. 小亮动手操作如下:如图,先剪一个等腰三角形纸片 ABC,使 AB = AC,再把 B 沿EM 折叠,使点 B 落在点 D 上;把∠C 沿 FN 折叠,使点 C 落在点 D 上,则四边形 AEDF是平行四边形,你认为正确吗?请说明理由.
A
B
C
D
M
E
F
N
A
B
C
D
M
E
F
N
证明 ∵ AB = AC,∴ ∠B = ∠C.
又由题意得 ∠B = ∠BDE,∠C = ∠CDF.
∠DEA = ∠B + ∠BDE,∠DFA = ∠C + ∠CDF.
∴∠DEA = ∠EFA.
又∵∠EDF + ∠BDE + ∠CDF = 180°,
∠A + ∠B +∠C = 180°
∴∠A = ∠EDF.
∴四边形 AEDF 是平行四边形.
4. 如图,在△ABC 中,∠ACB = 90°,D、F 分别为 AC、AB 的中点,点 E 在 BC 的延长线上,∠CDE =∠A.
求证:四边形 DECF 是平行四边形;
A
B
C
D
E
F
证明:∵点 D、F 分别是 AC、AB 的中点, ∴DF 是△ABC 的中位线,∴DF // CB. ∴∠ADF =∠ACB = 90° ∵AD = CD,∠ADF =∠CDF = 90°,DF = DF, ∴△ADF ≌△CDF ,∴∠A = ∠FCD. ∵∠CDE = ∠A, ∴∠FCD =∠CDE,∴FC // DE. ∴四边形 DECF 是平行四边形.
A
B
C
D
E
F
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
章末复习
华东师大版八年级数学下册
知识框架
平行四边形
对边相等、对边平行
对角线互相平分
对角相等、邻角互补
中心对称图形
两组对边分别平行
两组对边分别相等
一组对边平行且相等
对角线互相平分
两组对角分别相等
性质
判定
知识梳理
平行四边形的性质定理:
平行四边形的性质定理 1 平行四边形的对边相等.
平行四边形的性质定理 2 平行四边形的对角相等.
性
质
平行线的性质:
平行线之间的距离处处相等.
平行线的性质定理 3 平行四边形的对角线互相平分.
判
定
1. 两组对边分别平行的四边形是平行四边形
2. 两组对边分别相等的四边形是平行四边形
3. 一组对边平行且相等的四边形是平行四边形
4. 两组对角分别相等的四边形是平行四边形
5.两条对角线互相平分的四边形是平行四边形
例1 如图,点 E、F 是□ABCD 对角线上两点,在条件:①DE = BF;②∠ADE =∠CBF;③AF = CE;④∠AEB =∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加的条件是( )
A. ①②③
B. ①②④
C. ①③④
D. ②③④
D
例2 如图,已知点 E、C 在线段 BF 上,BE = CF,∠B =∠DEF,∠ACB =∠F,求证:四边形ABED 是平行四边形.
证明:∵BE = CF,
∴BE + EC = CF + EC,即BC = EF,
又∵∠B =∠DEF,∠ACB =∠F,
∴△ABC ≌△DEF,
∴AB = DE,
∵∠B =∠DEF,
∴AB∥DE,
∴四边形ABED是平行四边形.
例3 如图,直线 l1∥l2,△ABC 的面积为 10,则△DBC 的面积( )
A. 大于 10
B. 小于 10
C. 等于 10
D. 不确定
l1
l2
A
B
C
D
C
例4 如图,已知 E,F 是四边形 ABCD 的对角线 AC 上的两点,AE = CF,BE = FD,BE // FD. 求证:四边形 ABCD 是平行四边形.
A
B
C
D
E
F
A
B
C
D
E
F
O
证明 连结 BF ,DE,BD与 AC 交于点 O.
∵ BE = FD,BE // FD ,
∴四边形 BEDF 是平行四边形.
∴OB = OD,OE = OF.
又∵ AE = CF ,
∴AO =CO.
∴四边形 ABCD 是平行四边形.
随堂演练
1. 如图,平行四边形 ABCD 中,∠A 的平分线 AE 交 CD 于 E,AB = 5,BC = 3,则 EC 的长是( )
A. 1 B. 2
C. 1.5 D. 3
B
2. 如图, ABCD 的对角线相交于点 O,且 AB ≠ AD,过点 O 作 OE⊥BD 交 BC于点 E. 若△CDE 的周长为 10,则 ABCD 的周长为________.
A
B
C
D
O
E
20
3. 小亮动手操作如下:如图,先剪一个等腰三角形纸片 ABC,使 AB = AC,再把 B 沿EM 折叠,使点 B 落在点 D 上;把∠C 沿 FN 折叠,使点 C 落在点 D 上,则四边形 AEDF是平行四边形,你认为正确吗?请说明理由.
A
B
C
D
M
E
F
N
A
B
C
D
M
E
F
N
证明 ∵ AB = AC,∴ ∠B = ∠C.
又由题意得 ∠B = ∠BDE,∠C = ∠CDF.
∠DEA = ∠B + ∠BDE,∠DFA = ∠C + ∠CDF.
∴∠DEA = ∠EFA.
又∵∠EDF + ∠BDE + ∠CDF = 180°,
∠A + ∠B +∠C = 180°
∴∠A = ∠EDF.
∴四边形 AEDF 是平行四边形.
4. 如图,在△ABC 中,∠ACB = 90°,D、F 分别为 AC、AB 的中点,点 E 在 BC 的延长线上,∠CDE =∠A.
求证:四边形 DECF 是平行四边形;
A
B
C
D
E
F
证明:∵点 D、F 分别是 AC、AB 的中点, ∴DF 是△ABC 的中位线,∴DF // CB. ∴∠ADF =∠ACB = 90° ∵AD = CD,∠ADF =∠CDF = 90°,DF = DF, ∴△ADF ≌△CDF ,∴∠A = ∠FCD. ∵∠CDE = ∠A, ∴∠FCD =∠CDE,∴FC // DE. ∴四边形 DECF 是平行四边形.
A
B
C
D
E
F
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
