2022-2023学年北师大版九年级数学下册3.9 弧长及扇形的面积同步练习(含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学下册3.9 弧长及扇形的面积同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 11:14:13 | ||
图片预览

文档简介
九下-3.9 弧长及扇形的面积
一、选择题(共7小题)
1. 的圆心角对的弧长是 ,则此弧所在圆的半径是
A. B. C. D.
2. 如图,点 是 外接圆的圆心,若 的半径为 ,,则 的长是
A. B. C. D.
3. 如图,半圆的圆心为 ,直径 的长为 , 为半圆上一点,, 的长是
A. B. C. D.
4. 弧长等于半径的圆弧所对的圆心角是
A. B. C. D.
5. 如图,点 是以 为直径的半圆 的三等分点,,则图中阴影部分的面积是
A. B. C. D.
6. 如图,在 的正方形网格中,每个小正方形的边长都是 ,若将 绕点 顺时针旋转 得到 ,则 点运动的路径 的长为
A. B. C. D.
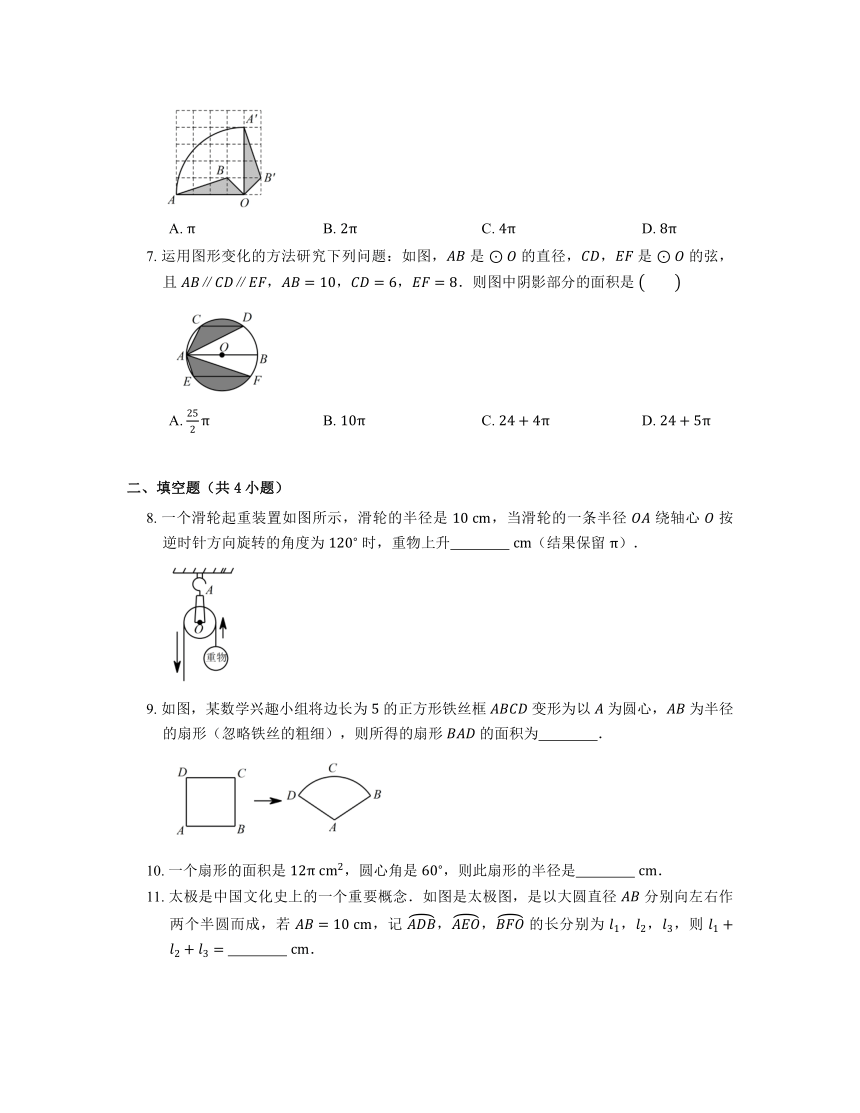
7. 运用图形变化的方法研究下列问题:如图, 是 的直径,, 是 的弦,且 ,,,.则图中阴影部分的面积是
A. B. C. D.
二、填空题(共4小题)
8. 一个滑轮起重装置如图所示,滑轮的半径是 ,当滑轮的一条半径 绕轴心 按逆时针方向旋转的角度为 时,重物上升 (结果保留 ).
9. 如图,某数学兴趣小组将边长为 的正方形铁丝框 变形为以 为圆心, 为半径的扇形(忽略铁丝的粗细),则所得的扇形 的面积为 .
10. 一个扇形的面积是 ,圆心角是 ,则此扇形的半径是 .
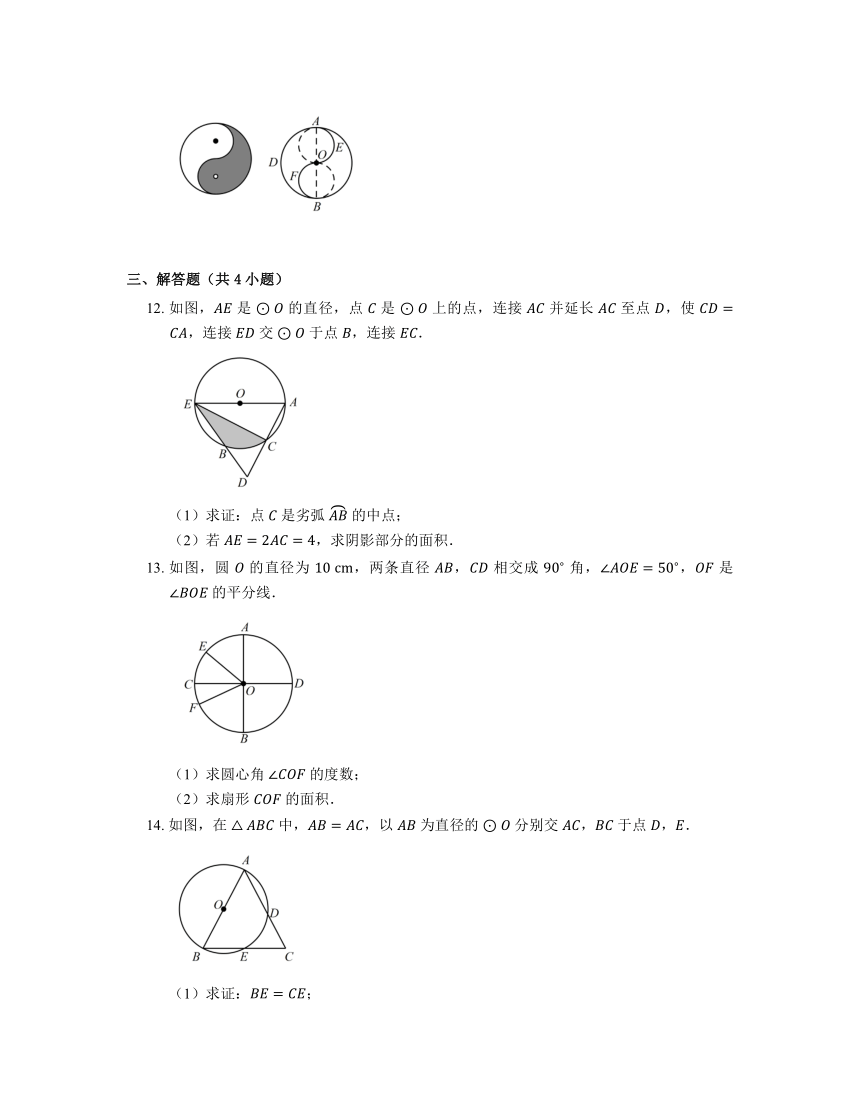
11. 太极是中国文化史上的一个重要概念.如图是太极图,是以大圆直径 分别向左右作两个半圆而成,若 ,记 ,, 的长分别为 ,,,则 .
三、解答题(共4小题)
12. 如图, 是 的直径,点 是 上的点,连接 并延长 至点 ,使 ,连接 交 于点 ,连接 .
(1)求证:点 是劣弧 的中点;
(2)若 ,求阴影部分的面积.
13. 如图,圆 的直径为 ,两条直径 , 相交成 角,, 是 的平分线.
(1)求圆心角 的度数;
(2)求扇形 的面积.
14. 如图,在 中,,以 为直径的 分别交 , 于点 ,.
(1)求证:;
(2)若 ,,求 的长.
15. 归纳猜想:同学们,让我们一起进行一次研究性学习:
(1)如图 ,已知正三角形 的中心为 ,半径为 ,将其沿直线 向右翻滚,当正三角形翻滚一周时,其中心 经过的路程是多少
(2)如图 ,将半径为 的正方形沿直线 向右翻滚,当正方形翻滚一周时,其中心 经过的路程是多少
(3)猜想:把正多边形翻滚一周,其中心 所经过的路程是多少( 为正多边形的半径,可参看图 ) 请说明理由.
答案
1. C
2. D
3. D
4. B
5. A
6. B
7. A
8.
9.
10.
11.
12. (1) 因为 是 的直径,
所以 .
因为 ,
所以 ,
所以 ,
所以 ,
所以点 是劣弧 的中点.
(2) 连接 ,,,
因为 ,
所以 ,,
所以 ,
所以 是等边三角形,
所以 ,
所以 .
因为 ,
所以 ,
所以 ,
所以 ,,
所以 ,
所以 .
13. (1) 因为 ,,
所以 .
因为 是 的平分线,
所以 .
因为两条直径 , 相交成 角,
所以 .
(2) 因为 的面积为 ,
所以扇形 的面积为 .
14. (1) 如图,连接 .
是圆 的直径,
,即 .
又 ,
是边 上的中线,
.
(2) 连接 ,
,
.
又 ,,
,
的长为 .
15. (1) 当正三角形 向右翻滚一周时,其中心 经过的路线是三条等弧,
其中心 经过的路程为 .
(2) 中心 经过的路程为 .
(3) 当 边形向右翻滚一周时,其中心 经过的路线是 条等弧,这些弧的半径为 ,所对的圆心角为 ,
中心 经过的路程为 .
一、选择题(共7小题)
1. 的圆心角对的弧长是 ,则此弧所在圆的半径是
A. B. C. D.
2. 如图,点 是 外接圆的圆心,若 的半径为 ,,则 的长是
A. B. C. D.
3. 如图,半圆的圆心为 ,直径 的长为 , 为半圆上一点,, 的长是
A. B. C. D.
4. 弧长等于半径的圆弧所对的圆心角是
A. B. C. D.
5. 如图,点 是以 为直径的半圆 的三等分点,,则图中阴影部分的面积是
A. B. C. D.
6. 如图,在 的正方形网格中,每个小正方形的边长都是 ,若将 绕点 顺时针旋转 得到 ,则 点运动的路径 的长为
A. B. C. D.
7. 运用图形变化的方法研究下列问题:如图, 是 的直径,, 是 的弦,且 ,,,.则图中阴影部分的面积是
A. B. C. D.
二、填空题(共4小题)
8. 一个滑轮起重装置如图所示,滑轮的半径是 ,当滑轮的一条半径 绕轴心 按逆时针方向旋转的角度为 时,重物上升 (结果保留 ).
9. 如图,某数学兴趣小组将边长为 的正方形铁丝框 变形为以 为圆心, 为半径的扇形(忽略铁丝的粗细),则所得的扇形 的面积为 .
10. 一个扇形的面积是 ,圆心角是 ,则此扇形的半径是 .
11. 太极是中国文化史上的一个重要概念.如图是太极图,是以大圆直径 分别向左右作两个半圆而成,若 ,记 ,, 的长分别为 ,,,则 .
三、解答题(共4小题)
12. 如图, 是 的直径,点 是 上的点,连接 并延长 至点 ,使 ,连接 交 于点 ,连接 .
(1)求证:点 是劣弧 的中点;
(2)若 ,求阴影部分的面积.
13. 如图,圆 的直径为 ,两条直径 , 相交成 角,, 是 的平分线.
(1)求圆心角 的度数;
(2)求扇形 的面积.
14. 如图,在 中,,以 为直径的 分别交 , 于点 ,.
(1)求证:;
(2)若 ,,求 的长.
15. 归纳猜想:同学们,让我们一起进行一次研究性学习:
(1)如图 ,已知正三角形 的中心为 ,半径为 ,将其沿直线 向右翻滚,当正三角形翻滚一周时,其中心 经过的路程是多少
(2)如图 ,将半径为 的正方形沿直线 向右翻滚,当正方形翻滚一周时,其中心 经过的路程是多少
(3)猜想:把正多边形翻滚一周,其中心 所经过的路程是多少( 为正多边形的半径,可参看图 ) 请说明理由.
答案
1. C
2. D
3. D
4. B
5. A
6. B
7. A
8.
9.
10.
11.
12. (1) 因为 是 的直径,
所以 .
因为 ,
所以 ,
所以 ,
所以 ,
所以点 是劣弧 的中点.
(2) 连接 ,,,
因为 ,
所以 ,,
所以 ,
所以 是等边三角形,
所以 ,
所以 .
因为 ,
所以 ,
所以 ,
所以 ,,
所以 ,
所以 .
13. (1) 因为 ,,
所以 .
因为 是 的平分线,
所以 .
因为两条直径 , 相交成 角,
所以 .
(2) 因为 的面积为 ,
所以扇形 的面积为 .
14. (1) 如图,连接 .
是圆 的直径,
,即 .
又 ,
是边 上的中线,
.
(2) 连接 ,
,
.
又 ,,
,
的长为 .
15. (1) 当正三角形 向右翻滚一周时,其中心 经过的路线是三条等弧,
其中心 经过的路程为 .
(2) 中心 经过的路程为 .
(3) 当 边形向右翻滚一周时,其中心 经过的路线是 条等弧,这些弧的半径为 ,所对的圆心角为 ,
中心 经过的路程为 .
