2022-2023学年冀教版八年级数学下册 第十九章 平面直角坐标系课后测评(无答案)
文档属性
| 名称 | 2022-2023学年冀教版八年级数学下册 第十九章 平面直角坐标系课后测评(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 281.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 11:21:15 | ||
图片预览


文档简介
第十九章 平面直角坐标系课后测评
一、单选题
1、在平面直角坐标系中,已知a<0, b>0, 则点P(a,b)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、点与点Q关于y轴对称,则点Q的坐标为( )
A. B. C. D.
3、下列命题中为真命题的是( )
A.三角形的一个外角等于两内角的和
B.是最简二次根式
C.数,,都是无理数
D.已知点E(1,a)与点F(b,2)关于x轴对称,则a+b=﹣1
4、如果点P(﹣5,b)在第二象限,那么b的取值范围是( )
A.b≥0 B.b≤0 C.b<0 D.b>0
5、在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A. B. C. D.
6、平面直角坐标系中,点P(2,1)关于x轴对称的点的坐标是( )
A. B. C. D.
7、如图所示,在平面直角坐标系xOy中,△ABC关于直线y=1对称,已知点A的坐标是(3,4),则点B的坐标是( )
A.(3,﹣4) B.(﹣3,2) C.(3,﹣2) D.(﹣2,4)
8、下列命题为真命题的是( )
A.过一点有且只有一条直线与已知直线平行 B.在同一平面内,若,,则
C.的算术平方根是9 D.点一定在第四象限
二、填空题
1、如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,0),“炮”位于点(﹣1,1),则“马”位于点______.
2、在平面直角坐标系中,把点向右平移2个单位到点B,则点B位于第______象限.
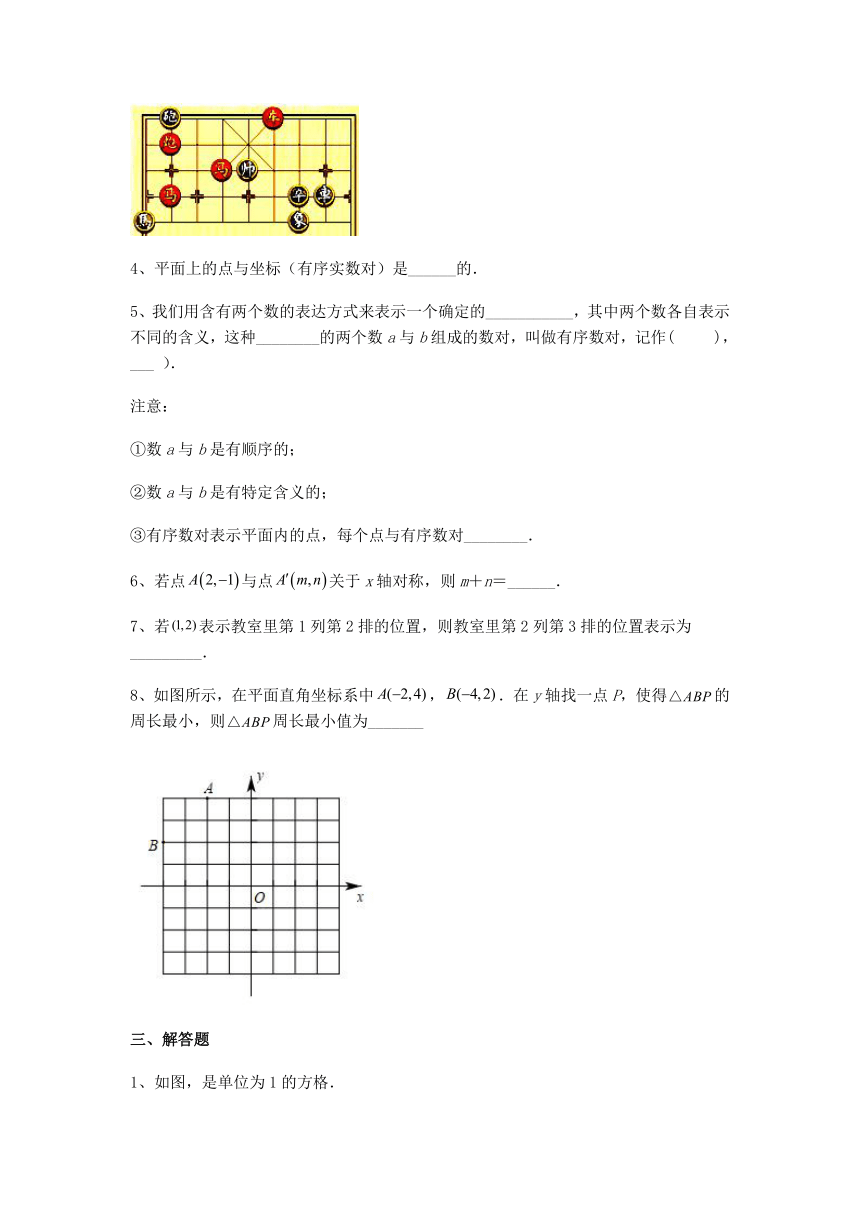
3、中国象棋是一个有悠久历史的游戏.如图的棋盘上,可以把每个棋子看作是恰好在某个正方形顶点上的一个点,若棋子“帅”对应的数对,棋子“象”对应的数对,则图中棋盘上“卒”对应的数对是_______
4、平面上的点与坐标(有序实数对)是______的.
5、我们用含有两个数的表达方式来表示一个确定的___________,其中两个数各自表示不同的含义,这种________的两个数a与b组成的数对,叫做有序数对,记作( ),___ ).
注意:
①数a与b是有顺序的;
②数a与b是有特定含义的;
③有序数对表示平面内的点,每个点与有序数对________.
6、若点与点关于x轴对称,则m+n=______.
7、若表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为_________.
8、如图所示,在平面直角坐标系中,.在y轴找一点P,使得的周长最小,则周长最小值为_______
三、解答题
1、如图,是单位为1的方格.
(1)在方格中建立直角坐标系,满足A,B两点的坐标分别是(0,2),(0,﹣2),并描出点C(2,﹣2),D(3,0),E(2,2),连接AB,BC,CD,DE,EA.
(2)作出(1)中五边形ABCDE关于y轴的对称图形.
(3)求(1)中所作的五边形ABCDE的周长和面积.
2、如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,0),B(﹣4,1),C(﹣2,2).
(1)直接写出点B关于原点对称的点B′的坐标: ;
(2)平移△ABC,使平移后点A的对应点A1的坐标为(2,1),请画出平移后的△A1B1C1;
(3)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2.
3、如图,在△ABC中,AC=2,AB=4,BC=6,点P为边BC上的一个动点(不与点B、C重合),点P关于直线AB的对称点为点Q,联结PQ、CQ,PQ与边AB交于点D.
(1)求∠B的度数;
(2)联结BQ,当∠BQC=90°时,求CQ的长;
(3)设BP=x,CQ=y,求y关于x的函数解析式,并写出函数的定义域.
4、如图,在平面直角坐标系中,点B,C,D的坐标分别是什么?
5、如图,的三个顶点都在边长为1的正方形网格的格点上,其中点B的坐标为,点C的坐标为.
(1)在网格中画出关于y轴对称的图形,并直接写出点的坐标;
(2)求线段的长.
一、单选题
1、在平面直角坐标系中,已知a<0, b>0, 则点P(a,b)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、点与点Q关于y轴对称,则点Q的坐标为( )
A. B. C. D.
3、下列命题中为真命题的是( )
A.三角形的一个外角等于两内角的和
B.是最简二次根式
C.数,,都是无理数
D.已知点E(1,a)与点F(b,2)关于x轴对称,则a+b=﹣1
4、如果点P(﹣5,b)在第二象限,那么b的取值范围是( )
A.b≥0 B.b≤0 C.b<0 D.b>0
5、在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A. B. C. D.
6、平面直角坐标系中,点P(2,1)关于x轴对称的点的坐标是( )
A. B. C. D.
7、如图所示,在平面直角坐标系xOy中,△ABC关于直线y=1对称,已知点A的坐标是(3,4),则点B的坐标是( )
A.(3,﹣4) B.(﹣3,2) C.(3,﹣2) D.(﹣2,4)
8、下列命题为真命题的是( )
A.过一点有且只有一条直线与已知直线平行 B.在同一平面内,若,,则
C.的算术平方根是9 D.点一定在第四象限
二、填空题
1、如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,0),“炮”位于点(﹣1,1),则“马”位于点______.
2、在平面直角坐标系中,把点向右平移2个单位到点B,则点B位于第______象限.
3、中国象棋是一个有悠久历史的游戏.如图的棋盘上,可以把每个棋子看作是恰好在某个正方形顶点上的一个点,若棋子“帅”对应的数对,棋子“象”对应的数对,则图中棋盘上“卒”对应的数对是_______
4、平面上的点与坐标(有序实数对)是______的.
5、我们用含有两个数的表达方式来表示一个确定的___________,其中两个数各自表示不同的含义,这种________的两个数a与b组成的数对,叫做有序数对,记作( ),___ ).
注意:
①数a与b是有顺序的;
②数a与b是有特定含义的;
③有序数对表示平面内的点,每个点与有序数对________.
6、若点与点关于x轴对称,则m+n=______.
7、若表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为_________.
8、如图所示,在平面直角坐标系中,.在y轴找一点P,使得的周长最小,则周长最小值为_______
三、解答题
1、如图,是单位为1的方格.
(1)在方格中建立直角坐标系,满足A,B两点的坐标分别是(0,2),(0,﹣2),并描出点C(2,﹣2),D(3,0),E(2,2),连接AB,BC,CD,DE,EA.
(2)作出(1)中五边形ABCDE关于y轴的对称图形.
(3)求(1)中所作的五边形ABCDE的周长和面积.
2、如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,0),B(﹣4,1),C(﹣2,2).
(1)直接写出点B关于原点对称的点B′的坐标: ;
(2)平移△ABC,使平移后点A的对应点A1的坐标为(2,1),请画出平移后的△A1B1C1;
(3)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2.
3、如图,在△ABC中,AC=2,AB=4,BC=6,点P为边BC上的一个动点(不与点B、C重合),点P关于直线AB的对称点为点Q,联结PQ、CQ,PQ与边AB交于点D.
(1)求∠B的度数;
(2)联结BQ,当∠BQC=90°时,求CQ的长;
(3)设BP=x,CQ=y,求y关于x的函数解析式,并写出函数的定义域.
4、如图,在平面直角坐标系中,点B,C,D的坐标分别是什么?
5、如图,的三个顶点都在边长为1的正方形网格的格点上,其中点B的坐标为,点C的坐标为.
(1)在网格中画出关于y轴对称的图形,并直接写出点的坐标;
(2)求线段的长.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
