第二章第五课时一元一次不等式(组)[下学期]
文档属性
| 名称 | 第二章第五课时一元一次不等式(组)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 296.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-12 16:33:00 | ||
图片预览








文档简介
课件20张PPT。精品
中考复习方案
数学分册第二章第五课时:
一元一次不等式(组) 要点、考点聚焦
课前热身
典型例题解析
课时训练要点、考点聚焦1.用不等号表示不等关系的式子叫做不等式. 2.一个含有未知数的不等式的所有的解,组成这个不
等式的解的集合,简称这个不等式的解集. 要点、考点聚焦3.不等式的性质
(1).不等式的两边都加上(或减去)同一个整式,不等号方向不变.
(2).不等式的两边都乘以(或除以)同一个正数,不等号方向不变.
(3).不等式的两边都乘以(或除以)同一个负数,不等号方向改变.
4.一元一次不等式
(1).只含有一个未知数,且未知数的次数是的一次的不等式叫做一元一次不等式.
(2).一元一次不等式的一般形式.
ax+b>0或ax+b<0(a≠0).
(3).解一元一次不等式的一般步骤(六环节一条龙):
①去分母;②去括号;③移项;④合并同类项;⑤系数化成1;⑥检验(检验步骤可以不写出来).5.一元一次不等式组
(1).几个一元一次不等式组成的一组不等式,叫做一元一次不等式组.
(2). 一元一次不等式组的解法:
①分别解每一个不等式;
②找出解集的公共部分(☆借助数轴法,☆规律推断法);
③写出不等式组的解集.
(3).数轴上表示解集时,要注意“空心圆圈”和“实心圆”的区别.6.求几个不等式解集的公共部分有如下规律:
(1)同大取大,如;
(2)同小取小,如;
(3)大于小的且小于大的取中间,如: 1<x<2
(4)小于小的且大于大的是空集,如: 无解.
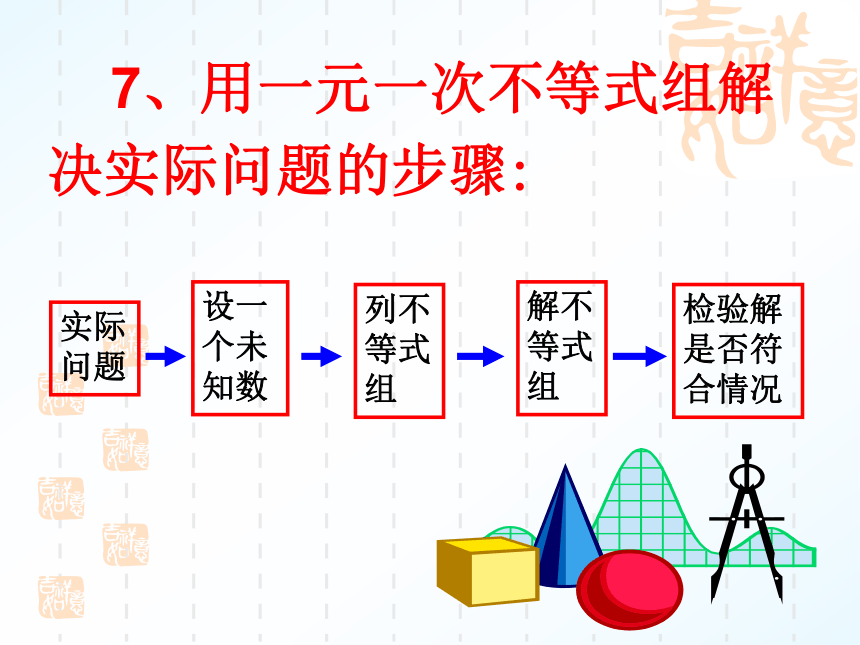
要点、考点聚焦 7、用一元一次不等式组解决实际问题的步骤:实际问题设一个未知数列不等式组解不等式组检验解是否符合情况课前热身1.(2004年·海淀区)不等式组 的解集为 ( )
A.x>-1 B.x<2
C.-1<x<2 D.x<-1或x>2Cx≤62.(2004年·天津市)不等式5x-9≤3(x+1)的解集是
.3.(2004年·上海市)不等式组 的整数解
是 .0、1 4.(2004年·南京市)解不等式组-3≤x≤35.(2003年·盐城市)解不等式组
并把解集在数轴上表示出来. ?
-7<x≤1.课前热身【例1】 解不等式: .典型例题解析x≥ 11/6【例2】 (2003年·河南省)不等式组
的整数解是 .4 直线y=(2m-3)x-4m+7过一、三、四象限,而点
A(-2,4)在第二象限,所以直线不通过点A.【例3】 已知:关于x的方程x2+(2m+1)x+m2+2=0有两个
不相等的实根,试判断直线y=(2m-3)x-4m+7能否通过点
A(-2,4),并说明理由.
典型例题分析例4、某次数学竞赛共20道题。每题答对得10分,答错或不答扣5分。至多答错或不答几道题,得分才能不低于80分?解:设至多答错或不答 x 题,依题意得解得,答:至多答错或不答 8 题,得分才能不低于80分。【例5】 甲、乙两车间同生产一种零件,甲车间有1人每天生产6件,其余每人每天生产11件,乙车间有1人每天生产7件,其余的生产10件,已知各车间生产的零件总数相等,且不少于100件不超过200件,求甲、乙车间各多少人?典型例题解析解:设甲车间有x人,乙车间有工人y人,则
6+11(x-1)=7+10(y-1)且100≤6+11(x-1)≤200
解得 ≤x≤
∴x可取10,11,12,13,14,15,16,17,18
∵y= 且为整数,
经检验:仅x=12符合题意.
∴y=13.故甲车间有12人,乙车间有13人 1.解不等式时,当在不等式两边同时乘以(或除以)一
个负数时,不等式的方向要立刻改变.
2.对于一些求特殊解(如整数解、正整数解、负整数
解等)的问题,应仔细辨别.
方法小结:课时训练1.(2003年·福州市)不等式组的解集是( )
A.x>-3 B.x≥2
C.-3<x≤2 D.x<-3B2.若不等式组的解集是x>a,则a的范围内( )
A.a<3 B.a=3
C.a>3 D.a≥3D3.不等式组
的整数解的和为( )
A.1 B.-1 C.0 D.-2C4:不等式组 的解集是( ) C 5、不等式组 的解集在数轴上的表示
正确的是 ( )D6、不等式组 的解集是
_________.2 ( )A、 -1 B、0 C、2 D、3A8:不等式组 的整数解为
_________。-3, -29.若x=1是不等式组
的解,求a的取值范围。10.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是( )
A.k<1/3 B.1/3<k<1
C.k>1 D.k>1或k<1/3
?
B课时训练11.(2003年·广州市)现计划把甲种货物120吨和乙种货物880吨用一列货车运往某地,
已知这列货车挂有A、B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x节,试写出y与x之间的函数关系式;
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
(3)在上述方案中,哪个方案运费最省?最少运费为多少元?
1.y=0.6x+0.8(40-x)=-0.2x+32 2.x取整数,故A型车厢可用24节或25节、26节;相应
的三种装车方案:①24节A型车厢和16节B型车厢;
②25节A型车厢和15节B型车厢;③26节A型车厢和14
节B型车厢.
3.安排A型车厢26节、B型车厢14节运费最省、最小
运费为26.8万元.
中考复习方案
数学分册第二章第五课时:
一元一次不等式(组) 要点、考点聚焦
课前热身
典型例题解析
课时训练要点、考点聚焦1.用不等号表示不等关系的式子叫做不等式. 2.一个含有未知数的不等式的所有的解,组成这个不
等式的解的集合,简称这个不等式的解集. 要点、考点聚焦3.不等式的性质
(1).不等式的两边都加上(或减去)同一个整式,不等号方向不变.
(2).不等式的两边都乘以(或除以)同一个正数,不等号方向不变.
(3).不等式的两边都乘以(或除以)同一个负数,不等号方向改变.
4.一元一次不等式
(1).只含有一个未知数,且未知数的次数是的一次的不等式叫做一元一次不等式.
(2).一元一次不等式的一般形式.
ax+b>0或ax+b<0(a≠0).
(3).解一元一次不等式的一般步骤(六环节一条龙):
①去分母;②去括号;③移项;④合并同类项;⑤系数化成1;⑥检验(检验步骤可以不写出来).5.一元一次不等式组
(1).几个一元一次不等式组成的一组不等式,叫做一元一次不等式组.
(2). 一元一次不等式组的解法:
①分别解每一个不等式;
②找出解集的公共部分(☆借助数轴法,☆规律推断法);
③写出不等式组的解集.
(3).数轴上表示解集时,要注意“空心圆圈”和“实心圆”的区别.6.求几个不等式解集的公共部分有如下规律:
(1)同大取大,如;
(2)同小取小,如;
(3)大于小的且小于大的取中间,如: 1<x<2
(4)小于小的且大于大的是空集,如: 无解.
要点、考点聚焦 7、用一元一次不等式组解决实际问题的步骤:实际问题设一个未知数列不等式组解不等式组检验解是否符合情况课前热身1.(2004年·海淀区)不等式组 的解集为 ( )
A.x>-1 B.x<2
C.-1<x<2 D.x<-1或x>2Cx≤62.(2004年·天津市)不等式5x-9≤3(x+1)的解集是
.3.(2004年·上海市)不等式组 的整数解
是 .0、1 4.(2004年·南京市)解不等式组-3≤x≤35.(2003年·盐城市)解不等式组
并把解集在数轴上表示出来. ?
-7<x≤1.课前热身【例1】 解不等式: .典型例题解析x≥ 11/6【例2】 (2003年·河南省)不等式组
的整数解是 .4 直线y=(2m-3)x-4m+7过一、三、四象限,而点
A(-2,4)在第二象限,所以直线不通过点A.【例3】 已知:关于x的方程x2+(2m+1)x+m2+2=0有两个
不相等的实根,试判断直线y=(2m-3)x-4m+7能否通过点
A(-2,4),并说明理由.
典型例题分析例4、某次数学竞赛共20道题。每题答对得10分,答错或不答扣5分。至多答错或不答几道题,得分才能不低于80分?解:设至多答错或不答 x 题,依题意得解得,答:至多答错或不答 8 题,得分才能不低于80分。【例5】 甲、乙两车间同生产一种零件,甲车间有1人每天生产6件,其余每人每天生产11件,乙车间有1人每天生产7件,其余的生产10件,已知各车间生产的零件总数相等,且不少于100件不超过200件,求甲、乙车间各多少人?典型例题解析解:设甲车间有x人,乙车间有工人y人,则
6+11(x-1)=7+10(y-1)且100≤6+11(x-1)≤200
解得 ≤x≤
∴x可取10,11,12,13,14,15,16,17,18
∵y= 且为整数,
经检验:仅x=12符合题意.
∴y=13.故甲车间有12人,乙车间有13人 1.解不等式时,当在不等式两边同时乘以(或除以)一
个负数时,不等式的方向要立刻改变.
2.对于一些求特殊解(如整数解、正整数解、负整数
解等)的问题,应仔细辨别.
方法小结:课时训练1.(2003年·福州市)不等式组的解集是( )
A.x>-3 B.x≥2
C.-3<x≤2 D.x<-3B2.若不等式组的解集是x>a,则a的范围内( )
A.a<3 B.a=3
C.a>3 D.a≥3D3.不等式组
的整数解的和为( )
A.1 B.-1 C.0 D.-2C4:不等式组 的解集是( ) C 5、不等式组 的解集在数轴上的表示
正确的是 ( )D6、不等式组 的解集是
_________.2
_________。-3, -29.若x=1是不等式组
的解,求a的取值范围。10.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是( )
A.k<1/3 B.1/3<k<1
C.k>1 D.k>1或k<1/3
?
B课时训练11.(2003年·广州市)现计划把甲种货物120吨和乙种货物880吨用一列货车运往某地,
已知这列货车挂有A、B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x节,试写出y与x之间的函数关系式;
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
(3)在上述方案中,哪个方案运费最省?最少运费为多少元?
1.y=0.6x+0.8(40-x)=-0.2x+32 2.x取整数,故A型车厢可用24节或25节、26节;相应
的三种装车方案:①24节A型车厢和16节B型车厢;
②25节A型车厢和15节B型车厢;③26节A型车厢和14
节B型车厢.
3.安排A型车厢26节、B型车厢14节运费最省、最小
运费为26.8万元.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
