11.3 用反比例函数解决问题

课件29张PPT。11.3　用反比例函数解决问题（1）八年级(下册)初中数学苏科版挑战记忆反比例函数图象有哪些性质?反比例函数 是由两支曲线组成,当K>0时,两支曲线分别位于第一、三象限内，在每一象限内，y随x的增大而减少；当K<0时,两支曲线分别位于第二、四象限内,在每一象限内,y随x的增大而增大. 你吃过拉面吗？你知道在做拉面的过程中渗透着数学知识吗？ （1）体积为20cm3的面团做成拉面，面条的总长度y与面条粗细（横截面积）s有怎样的函数关系？ （2）某家面馆的师傅手艺精湛，他拉的面条粗1mm2，面条总长是多少？ 创设情景 3月踏青的季节，我校组织八年级学生去北山春游，从学校出发到山脚全程约为120千米，
（1）汽车的速度v与时间t有怎样的函数关系？
（2）原计划8点出发，11点到，但为了提前一个小时到达能参观南岩一个活动，平均车速应多快？ 归纳　　问题1　小明要把一篇24000字的社会调查报告录入电脑．
　　（1）如果小明以每分钟 120 字的速度录入，他需要多长时间才能完成录入任务？ 解：（1） 　 　．
所以完成录入任务需 200 min ．　　问题1　小明要把一篇24000字的社会调查报告录入电脑．
　　（2）完成录入的时间t（分）与录入文字的速度v（字/分）有怎样的函数关系？ 　　解：（2）由v · t＝24000，得 　　　　．
　　所以完成录入的时间 t 是录入文字的速度 v 的反比例函数．　　问题1 小明要把一篇24000字的社会调查报告录入电脑．
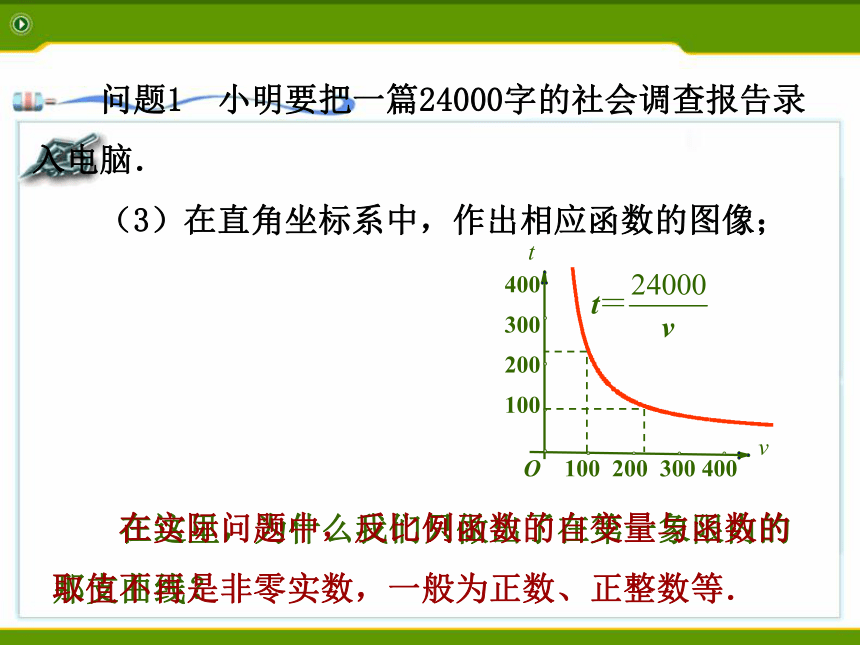
　　（3）在直角坐标系中，作出相应函数的图像；vtO 100 200 300 400400 300 200 100　　在这里，为什么我们只做出了在第一象限内的那支曲线？　　在实际问题中，反比例函数的自变量与函数的取值不再是非零实数，一般为正数、正整数等．　　问题1　小明要把一篇24000字的社会调查报告录入电脑．
　　（4）要在3 h 内完成录入任务，小明每分钟至少应录入多少个字？　　解：（4）把t＝180代入v·t＝24000，得
　　　≈133.3．
　　小明每分钟至少应录入134字，才能在3 h 内完成录入任务． 在函数求值的过程中，要注意单位的一致．　　问题1　小明要把一篇24000字的社会调查报告录入电脑．
　　（4）要在3 h 内完成录入任务，小明每分钟至少应录入多少个字？　　解：（4）把t＝180代入v·t＝24000，得
　　　≈133.3．
　　小明每分钟至少应录入134字，才能在3 h 内完成录入任务．　　本题 v 的取值为正整数，我们需对计算结果“进一”, 作为实际问题的解．　　问题1　小明要把一篇24000字的社会调查报告录入电脑．
　　（4）要在3 h 内完成录入任务，小明每分钟至少应录入多少个字？你能利用图像对此作出直观解释吗？vtO 100 200 300 400400 300 200 100 我们在函数图像上找到当 t ＝180 的点，此时在这个点下侧也就是右侧的函数图像所对应的 v 值都是满足要求的 . 结合实际意义，此时 v 为≥134的正整数．函数图像可以直观的解决数学问题．　　问题2　某厂计划建造一个容积为4×104m3的长方形蓄水池．
　　（1）蓄水池的底面积 S(m2)与其深度 h(m)有怎样的函数关系？ 解：（1）由Sh＝4×104，得 　 ．
蓄水池的底面积S是其深度 h 的反比例函数．　　解：（2）把h＝5代入 ，得
　　　　　　　　　　　　　　．
　　当蓄水池的深度设计为5 m 时，它的底面积应为8000m2． 　本题中给出了 h 的值，求相应 S 的值，这是个求函数值的问题．　　问题2　某厂计划建造一个容积为4×104m3的长方形蓄水池．
　　（2）如果蓄水池的深度设计为5 m ，那么它的底面积应为多少？ 　问题2　某厂计划建造一个容积为4×104m3的长方形蓄水池．
　　（3）如果考虑绿化以及辅助用地的需要，蓄水池的长和宽最多只能分别设计为100m和60m，那么它的深度至少应为多少米（精确到0.01）？解：（3）根据题意，得S＝100×60＝6000．
把 代入 ，得
≈ 6.667 ．
　　蓄水池的深度至少应为6.67 m ． 　你使劲踩过气球吗？为什么使劲踩气球，气球会发生爆炸？你能解释这个现象吗？ 　某气球内充满了一定量的气体，当温度不变时，气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数，其图像如图所示.
　　（1）你能写出这个函数表达式吗？ 解： （1） . 　你使劲踩过气球吗？为什么使劲踩气球，气球会发生爆炸？你能解释这个现象吗？ 　某气球内充满了一定量的气体，当温度不变时，气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数，其图像如图所示.
　　（2）当气体体积为1m3时，气压是多少？ 解：（2）当V＝1m3时，
　　 P＝ 　　 . 　你使劲踩过气球吗？为什么使劲踩气球，气球会发生爆炸？你能解释这个现象吗？ 　某气球内充满了一定量的气体，当温度不变时，气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数，其图像如图所示.
　　（3）当气球内的气压大于140kpa时，气球将爆炸，为了安全起见，气体的体积应不小于多少？ 解：（3）当P＝140时，
V＝ ≈0.686.
所以为了安全起见，气体的体积应不少于0.69m3．　　生活中还有许多反比例函数模型的实际问题，你能举出例子吗？小结：转化(反比例函数)解决老师寄语：
　　数学来源于生活，生活中处处有数学，
　　让我们学会用数学的眼光看待生活．11.3　用反比例函数解决问题（2） 你知道公元前3世纪古希腊学者阿基米德发现的著名的“杠杆原理”吗？ 杠杆平衡时，阻力×阻力臂＝动力×动力臂. 阿基米德曾豪言：给我一个支点，我能撬动地球.你能解释其中的道理吗？　　问题1　某报报道：一村民在清理鱼塘时被困淤泥中，消防队员以门板作船，泥沼中救人．
　　如果人和门板对淤泥地面的压力合计900N，而淤泥承受的压强不能超过600Pa，那么门板面积至少要多大？11.3　用反比例函数解决问题（2）　　解：设人和门板对淤泥的压强为p(Pa)，门板面积为S（m2），则 ．
　　把p＝600代入 ，得
．解得 S＝1.5．
　　根据反比例函数的性质，p随S的增大而减小，所以门板面积至少要1.5m2． 　问题2　某气球内充满了一定质量的气体，在温度
不变的条件下，气球内气体的压强p(Pa)是气球体积V（m3）的反比例函数，且当V ＝1.5m3时，p＝16000Pa．
　（1）当V ＝1.2m3时，求p的值；11.3　用反比例函数解决问题（2） 解：（1）设p与V的函数表达式为 ．
把p＝16000、V ＝1.5代入 ，得
．
解得：k＝24000．
p与V的函数表达式为 　．
当V＝1.2时， ＝20000．　　问题2　某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V（m3）的反比例函数，且当V ＝1.5m3时p＝16000Pa．
　　（2）当气球内的气压大于40000Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应不小于多少？解：（2）把p＝40000代入 　，得　　　　　 ．
　　　解得：V＝0.6．
　　根据反比例函数的性质，p随V的增大而减小．为确保气球不爆炸，气球的体积应不小于0.6m3． 11.3　用反比例函数解决问题（2）　　问题3　如图，阻力为1000N，阻力臂长为5cm.设动力y（N），动力臂为x（cm）（图中杠杆本身所受重力略去不计．杠杆平衡时：动力×动力臂=阻力×阻力臂）
　　（1）当x＝50时，求y的值，并说明这个值的实际意义；当x＝100时，求y的值， 并说明这个值的实际意义；当x ＝250呢？x ＝500呢？11.3　用反比例函数解决问题（2）　　问题3　如图，阻力为1000N，阻力臂长为5cm.设动力y（N），动力臂为x（cm）（图中杠杆本身所受重力略去不计．杠杆平衡时：动力×动力臂＝阻力×阻力臂）
　（2）当动力臂长扩大到原来的n倍时，所需动力将怎样变化？请大家猜想一下.11.3　用反比例函数解决问题（2） 　（3）如果动力臂缩小到原来的　　时，动力将怎样变化？为什么呢？　　某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系：
（1）根据表中的数据
在平面直角坐标系中描出实数对（x,y）的对应点.
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为w元，试求出w与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元／个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？练习小结：11.3　用反比例函数解决问题（2）